2015 - Politécnicos

ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
DEPARTAMENTO DE ENGENHARIA MECÂNICA
Mecânica II – PME 3200 – Prova de Recuperação – 23/07/2015
Duração da Prova: 100 minutos
(Não é permitido o uso de dispositivos eletro-eletrônicos)
1ª Questão (3,5 pontos) O anel homogêneo (de espessura
desprezível), de massa m e raio R gira ao redor da barra OG,
de massa desprezível e comprimento L, com velocidade
angular a ela relativa (i.e., de rotação própria) constante, ω.
Sabe-se que este rotor está em movimento de precessão
estacionária com ângulo θ e taxa de precessão Ω , ambos
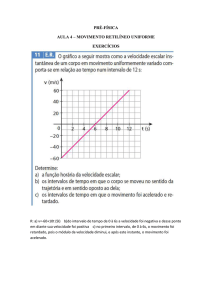
constantes e considerados conhecidos. O sistema Oxyz
acompanha a barra OG, com Oy sempre horizontal. Os eixos
Ox, Oy, Oz e OZ
são orientados respectivamente pelos
r r r r
versores, i , j , k e K . Nesta situação de equilíbrio dinâmico,
determine:
Ω
Z
z
ω
G
θ
g
L
O
y
x
(a) a velocidade angular de rotação própria, ω ;
(b) a força de reação aplicada ao sistema, pela rótula O.
2ª Questão (3,5 pontos) No sistema mostrado na figura,
o disco de centro O, massa M e raio R, rola sem
escorregar sobre o plano horizontal e está ligado a uma
parede vertical por meio de uma mola de rigidez k e de
um amortecedor viscoso linear de constante c. Um
pêndulo ideal, formado por uma pequena esfera de
massa m posicionada na extremidade de uma haste de
comprimento L e de massa desprezível, é acoplado ao
centro do disco. A mola tem deformação nula quando a
coordenada x vale zero. Uma força horizontal F(t) atua
no disco. Usando x e θ como coordenadas
generalizadas, pede-se:
(a)
(b)
(c)
(d)
(e)
M, R
x
k
O
F(t)
g
c
θ
L
m
A
a energia cinética do sistema;
a energia potencial do sistema;
a função de dissipação de Rayleigh, associada ao amortecedor;
as demais forças generalizadas não conservativas atuando sobre o sistema;
as equações de movimento para as coordenadas x e θ, usando o formalismo de Lagrange.
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
DEPARTAMENTO DE ENGENHARIA MECÂNICA
3ª Questão (3,0 pontos)
Durante a formação de um trem estacionado e imóvel (freio acionado) no pátio de manobras, um
r
r
vagão de massa total m se choca com velocidade constante VG = ui imediatamente anterior ao
choque. O contato
entre os vagões ocorre no ponto P, coincidente com o centro dos engates tal
r r
que ( P − G ) = ai − bj . Conhecido o coeficiente de restituição e, devido ao aparelho de choque e
tração do vagão e desprezando qualquer forma de atrito, pede-se:
VG
TREM ESTACIONADO
y
G
P
x
a)
b)
c)
d)
e)
elabore o diagrama de corpo-livre do vagão no instante do impacto;
equacione o problemar de impacto;
determine o impulso I aplicado no ponto P do vagão.
r
r
r
determine e a velocidade VG ′ = u ′i + v ′j , do centro de massa G do vagão, logo após o choque.
r
determine o vetor de rotação do vagão ω ′ , logo após o choque.
Dado: JGz, momento de inércia total do vagão em torno do eixo Gz no centro de massa.
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
DEPARTAMENTO DE ENGENHARIA MECÂNICA
Mecânica II – PME 3200 – Prova de Recuperação – 23/07/2015
Duração da Prova: 100 minutos
(Não é permitido o uso de dispositivos eletro-eletrônicos)
1ª Questão (3,5 pontos)
O anel homogêneo (de espessura desprezível), de massa m e raio
R gira ao redor da barra OG, de massa desprezível e comprimento
L, com velocidade angular a ela relativa (i.e., de rotação própria)
constante, ω. Sabe-se que este rotor está em movimento de
precessão estacionária com ângulo θ e taxa de precessão Ω,
ambos constantes e considerados conhecidos. O sistema Oxyz
acompanha a barra OG, com Oy sempre horizontal. Os eixos Ox,
Oy, Oz e OZ são orientados respectivamente pelos versores,
r r r r
i , j , k e K . Nesta situação de equilíbrio dinâmico, determine:
Ω
Z
z
ω
G
θ
g
L
O
y
(a) a velocidade angular de rotação própria, ω;
(b) a força de reação aplicada ao sistema, pela rótula O.
x
Resolução:
a)
r
r
r
r
r
r
r
r
ωabs = ωarr + ω rel = ΩK + ωk ; mas K = cos θ k − sen θ i , logo:
r
r
r
ωabs = (ω + Ω cos θ ) k − Ω sen θ i
(0,5)
Da condição de precessão estacionária, (φ& = Ω = cte; ψ& = ω = cte; θ& ≡ 0) , pode-se deduzir, pelo TMA,
r&
r
H O = M Oext , com O fixo, um ponto pertencente à extensão ideal rígida do anel , que:
( Jω + ( J − I )Ω cos θ )Ω = mgzG = mgL
(1,5)
de onde:
ω=
 R2

mgL
I
+ ( − 1)Ω cos θ ; com J = mR 2 e I = m
+ L2  .
JΩ
J
 2

ω=
Ou seja:
gL  L2 1 
+
− Ω cos θ
ΩR 2  R 2 2 
(0,5)
r
r
r
r
r
b) Neste caso de precessão estacionária ( ωarr = ΩK = cte ), tem-se: aG = ω arr ∧ (ωarr ∧ (G − O) ) , de forma
r
r
r
r
r
r
r
r
que: aG = ΩK ∧ ΩK ∧ Lk = ΩK ∧ ΩLsenθj = Ω 2 Lsenθ( K ∧ j ) , i.e.,
(
)
(
)
r
r
r
aG = −Ω 2 Lsenθ cos θi + sen θk
(
)
r
v r
Do TMB seguem as reações, Xi + Yj + Zk , aplicadas pela articulação ao sistema.
(0,5)
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
DEPARTAMENTO DE ENGENHARIA MECÂNICA
r
r
v r
r
De fato: maG = Xi + Yj + Zk − mgK , ou seja,
r
r
r
r
r
v r
− mΩ2 Lsenθ cosθi + sen θk = Xi + Yj + Zk − mg ( −senθi + cos θk )
(
)
Tal que:


Ω2 L
X = − mg  sen θ +
sen θ cos θ 
g


Y =0
.
(0,5)


Ω L
Z = mg  cos θ −
sen 2 θ 
g


2
2ª Questão (3,5 pontos)
No sistema mostrado na figura, o disco de centro O,
massa M e raio R, rola sem escorregar sobre o plano
horizontal e está ligado a uma parede vertical por meio
de uma mola de rigidez k e de um amortecedor viscoso
linear de constante c. Um pêndulo ideal, formado por
uma pequena esfera de massa m posicionada na
extremidade de uma haste de comprimento L e de
massa desprezível, é acoplado ao centro do disco. A
mola tem deformação nula quando a coordenada x vale
zero. Uma força horizontal F(t) atua no disco. Usando
M, R
x
k
F(t)
O
g
c
θ
L
m
A
x e θ como coordenadas generalizadas, pede-se:
(a)
(b)
(c)
(d)
(e)
a energia cinética do sistema;
a energia potencial do sistema;
a função de dissipação de Rayleigh, associada ao amortecedor;
as demais forças generalizadas não conservativas atuando sobre o sistema;
as equações de movimento para as coordenadas x e θ, usando o formalismo de Lagrange.
Resolução:
(a)
Energia Cinética:
T = TD + TA
(D:disco; A: pêndulo)
Disco, s/ escorregamento (C=CIR):
TD =
1
1 3MR 2 2 3MR 2 2
ICΩ2 =
Ω =
Ω .
2
2 2
4
Energia cinética do pêndulo:
TA =
1
2
mv A .
2
Mas,
r
r
r
v A = ( x& + θ&L cos θ )i + (θ&L sin θ ) j ; então:
Portanto:
TA =
1 
1
3
T =  M + m  x& 2 + mx&θ&L cos θ + mθ& 2 L2 .
2 
2
4
1
m x& 2 + 2 x&θ&L cos θ + θ& 2 L2 .
2
(
)
(1,0)
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
DEPARTAMENTO DE ENGENHARIA MECÂNICA
(b)
Energia Potencial:
(c)
Rayleighiana:
R=
V=
1 2
kx + mgL(1 − cos θ ) .
2
(0,5)
1 2
Cx& .
2
(0,5)
(d) Forças generalizadas outras (exceto as conservativas ou as dissipativas de Rayleigh):
Qx = F ;
.
(0,5)
QΘ = 0
(e) Aplicando a equação de Lagrange:
d  ∂T
dt  ∂q& j
 ∂T ∂V ∂R
−
+
+
= Q j vem:
 ∂q
∂q j ∂q& j
j

3

2
 M + m  &x& + (mL cos θ )θ&& − mLθ& sin θ + Cx& + kx = F
2

.
(mL cos θ )&x&
+
2 &&
mL θ
+
mgL sin θ
(1,0)
= 0
Resolução da 3a. Questão (3,0 pontos)
Durante a formação de um trem estacionado e imóvel (freio acionado) no pátio de manobras, um
r
r
vagão de massa total m se choca com velocidade constante VG = ui imediatamente anterior ao
choque. O contacto entre os vagões ocorre no ponto P, coincidente com o centro dos engates tal
r r
que ( P − G ) = ai − bj . Conhecido o coeficiente de restituição e, devido ao aparelho de choque e
tração do vagão e desprezando qualquer forma de atrito, pede-se:
VG
a) elabore o diagrama de corpo-livre do vagão;
para impacto sem atrito (0,5 pontos)
y
G
P
x
b) equacione o problema de impacto; Aplicando o TRI e o TMI no vagão:
TRI
I
 ′
r
r
r
 m( u ′ − u ) = − I
u = u −
m(VG′ − VG ) = − I i ⇒ 
⇒
m
 m ( v′ − v ) = 0
 v′ = 0
(3.1)
(0,5 pontos)
I
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
DEPARTAMENTO DE ENGENHARIA MECÂNICA
TMI
r
r r
r
Ib r
Ib
J Gz (ω ′ − ω ) = − I b k ⇒ ω ′ = −
k ⇒ ω′ = −
J Gz
J Gz
(3.2)
(0,5 pontos)
Da formula de campo de velocidades tem-se:
r
r
r
r Ib r
r r
r
VP′ = VG′ + ω ′ ∧ ( P − G ) → VP′ = u′ i −
k ∧ ( ai − bj )
J Gz
r 
r 
I  r Ib r r
I Ib 2  r Iab r
i −
VP′ =  u −  i −
(aj + bi ) → VP′ =  u − −
j
m
J Gz
m J Gz 
J Gz


Formula de restituição de Newton
r r
r r
VP′ ⋅ i = −eVP ⋅ i →
(3.3)

I Ib 2 
 u − −
 = −e u
m J Gz 

(3.4)
r
c) determine o impulso I aplicado no ponto P do vagão;
Utilizando (3.4):
I =u
(1 + e)m J Gz
( J Gz + mb 2 )
r
r
→
r
(1 + e)m J Gz r
I = −u
i
( J Gz + mb 2 )
(3.5)
(0,5 pontos)
r
d) determine e a velocidade VG′ = u ′ i + v ′ j , do centro de massa G do vagão:

(1 + e) J Gz 

u ′ = u 1 −
2 
 ( J Gz + mb ) 
r

(1 + e) J Gz  r
i
VG′ = u 1 −
2 
 ( J Gz + mb ) 
Utilizando (3.5) em (3.1)
Sabendo que (3.1):
v′ = 0
(0,5 pontos)
r
e) o vetor de rotação do vagão ω ′ , logo após o choque.
Utilizando (3.5) em (3.2):
ω ′ = −u
m b (1 + e)
J Gz + mb 2
(
)
(0,5 pontos)