Lista de Exercícios 1

MEC-483 – Vibrações Mecânicas
Prof. Fabiano Armellini
Lista de Exercícios 1
1) Uma massa de 0,453kg é montada na extremidade inferior de uma mola que, por
conta da ação da gravidade, elonga-se 7,87mm. Determinar a freqüência natural do
sistema.
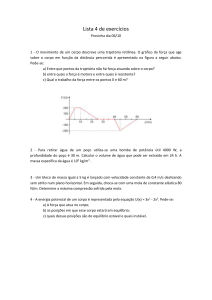
2) Para o sistema massa-mola da figura abaixo, desprezando-se o atrito, determinar:
g
k1
x
m
k2
a) A expressão da deflexão estática da mola (δ) que equilibra o sistema, em função de
m, g, k1, k2 e θ
b) A equação diferencial do movimento ao longo de x, medida a partir da posição de
equilíbrio estático
c) Os valores de massa efetiva (mef), rigidez efetiva (kef) e freqüência natural (ωn) do
sistema para k1=1000N/m, k2=750N/m, m=50kg e θ=π/3rad
3) A razão k/m para um sistema massa-mola é calculada em 4,0 (unidades implícitas).
Se em t0 a massa é defletida 2cm para baixo, medida a partir da sua posição de
equilíbrio estático, e é imposta uma velocidade inicial de 8cm/s para cima, determinar
a amplitude de vibração e a máxima aceleração do sistema.
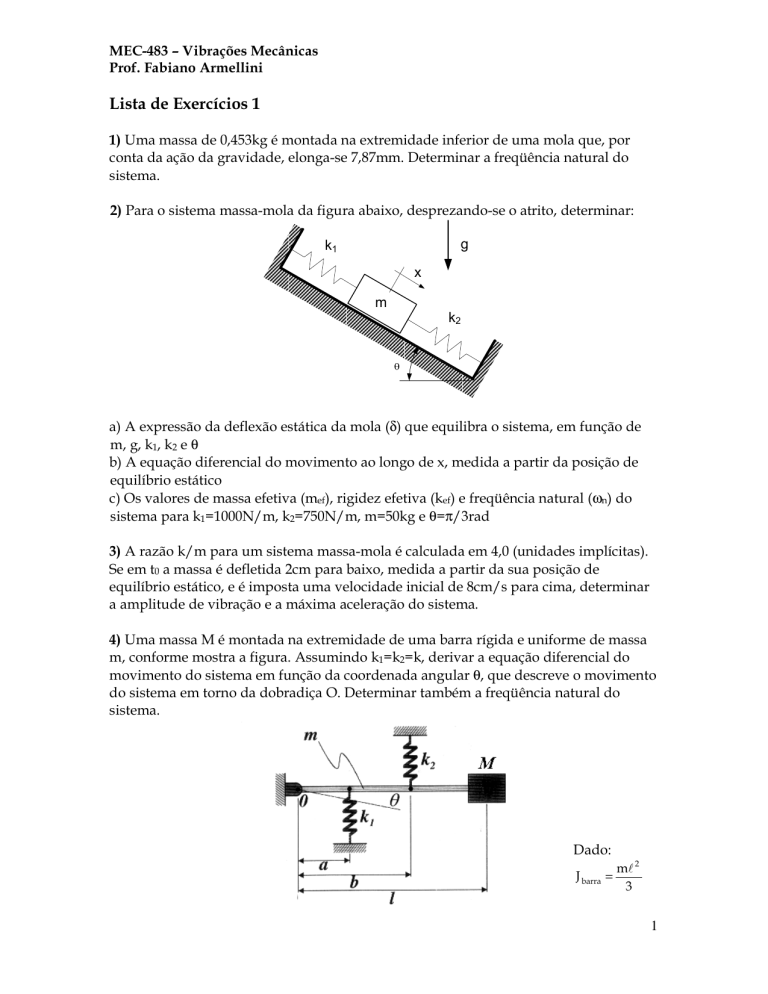
4) Uma massa M é montada na extremidade de uma barra rígida e uniforme de massa
m, conforme mostra a figura. Assumindo k1=k2=k, derivar a equação diferencial do
movimento do sistema em função da coordenada angular θ, que descreve o movimento
do sistema em torno da dobradiça O. Determinar também a freqüência natural do
sistema.
Dado:
J barra =
ml 2
3
1
5) No regulador de velocidade de Hartnell da figura abaixo, a rigidez da mola é dada
por k=104N/m e o peso de cada esfera é de 25N. A distância do pivô da alavanca do
mecanismo às esferas é r=20cm e à bucha do eixo de rotação é a=12cm. A distância
entre o pivô e o eixo de rotação é b=16cm. A mola encontra-se 1cm comprimida quando
o braço das esferas está vertical. Encontrar a velocidade de rotação Ω constante do
regulador para a qual o braço das esferas permanece vertical.
Fonte: Rao, S.S., Mechanical Vibrations, Addison
Wesley Publishing Company, 3ª ed., 1995, p.169.
2