Movimento em Várias Dimensões

Centro de Ciências Naturais e Humanas (CCNH)
Universidade Federal do ABC (UFABC)
Fenômenos Mecânicos – BC0208
Aula 20
Denise Criado
([email protected])
28/03/2013
O que veremos hoje...
Corpos Rígidos Rolando
 Teorema dos Eixos Paralelos
 Movimento de Precessão
Rolamento – Combinação de Translação e Rotação
O CM de uma roda que está rolando
percorre uma distância s com
velocidade vCM
Translação pura
Rotação pura
R
Translação +
rotação
R
s R
d
d
s   R    R
dt
dt

vCM   R
(rolamento sem deslizamento)
cicloide
Exemplo de rolamento
com deslizamento:
rotação + translação
movimento do CM
Rolamento visto como uma rotação pura
T
Qual o valor da velocidade angular da roda,
em torno de P, Para um observador estacionário?
vT    2 R   2  R   2vCM
vO   R  vCM
vP    0  0
Eixo de rotação em P

Atrito de rolamento (sem deslizamento)
Deformação exagerada
Não existe atrito de deslizamento
força de atrito não realiza trabalho
Devido à deformação causada pela esfera rígida
ao rolar plano abaixo, as forças de contato atuam
sobre diversos pontos. Há perda de energia mecânica.
Na situação de um cilindro girando, a força de atrito é estática em vez de cinética,
pois o ponto de contato do cilindro com a superfície está em repouso em relação á
superfície em qualquer instante.
Teorema dos Eixos Paralelos
Um Teorema útil, chamado de
Teorema dos Eixos Paralelos, nos
permite expressar a energia em
termos de Momento de Inércia I em
relação a qualquer eixo paralelo ao
eixo que passa pelo centro de massa
de um corpo. Esse teorema afirma
que:
I p  ICM  MD
2
onde, D é a distância do eixo paralelo até o
eixo do centro de massa, e M é a massa
total do corpo.
Teorema dos Eixos Paralelos
T
EX: Aplicação do teorema para expressar
um ponto de contato de um corpo rolando
sobre a superfície.
I p  ICM  MD2
Eixo de rotação em P
I p  ICM  MR
2
A distância desse ponto de contato
até o centro de massa do corpo
simétrico é seu RAIO.
Exemplo
Momento de Inércia de uma esfera maciça e homogênea
em relação a um eixo tangente a sua superfície
I  I CM
2
7
2
2
 MD  MR  MR  MR 2
5
5
2
Para uma barra homogênea de massa M e comprimento L, o momento de inércia em
relação a um eixo perpendicular ao plano da barra e que passa por uma extremidade
é I = 1/3 M L2. Calcular o momento de inércia em relação ao eixo que passa pela
metade da barra.
I CM
1
L 2 1
2
 I  MD  ML  M ( )  ML2
3
2
12
2
Momento de Inércia
Cilindro
anular (ou
anel) em
torno do eixo
central
Aro em torno
do eixo central
I  MR
2
(a)

1
I  M R12  R22
2

1
I  MR 2
2
(c)
1
1
I  MR 2  ML2
4
12
Bastão fino em
torno do eixo
central
perpendicular
ao seu
comprimento
1
I  12
ML2
(e)
(b)
Cilindro
sólido (ou
disco) em
torno do
diâmetro
central
Cilindro
sólido (ou
disco) em
torno do eixo
central
I  13 ML2
Esfera sólida
em relação a
um diâmetro
qualquer
I  52 MR 2
I  23 MR 2
(h)
Aro em relação
a um diâmetro
qualquer
(d)
Bastão fino em
torno do eixo
que passa por
uma das
extremidades
perpendicular
ao seu
comprimento(f)
(g)
Casca
eférica
delgada em
relação a um
diâmetro
qualquer
1
I  12
MR 2
(i)
Tábua em
relação a um
eixo central
ortogonal

1
I  12
M a 2  b2

(j)
Energia Cinética
Translação
Rotação
T
K  12 ICM  2  12 MvC2M
Usando vCM   R
Substituindo na equação de K:
Eixo de rotação em P
K  12 ICM  2  12 MR2 2
Usando o Teorema dos Eixos Paralelos:
I P  ICM  MR
K  I P
1
2
2
2
Energia cinética da roda, para
uma rotação pura em torno de
um eixo que passa por P
Velocidade de um ioiô primitivo
Um ioiô primitivo é feito enrolando-se um fio diversas vezes em torno de um cilindro de
massa M e raio R. Você mantém presa a extremidade do fio enquanto o cilindro é liberado
sem velocidade inicial. O fio se desenrola, mas não desliza nem dilata a medida que o
cilindro cai e gira. Use as considerações de energia para achar a velocidade de Vcm do centro
de massa do cilindro sólido depois que ele caiu até uma distancia h.
R

Velocidade de um ioiô primitivo
Não ocorre perda de energia mecânica pois o fio
não desliza sobre a superfície do cilindro
U1  Mgh
Energias potenciais
nos pontos 1 e 2
U2  0
R
K1  0
K 2  12 MvC2M  12 I CM  2

2
K 2  12 MvCM

1
2

1
2
Energias cinéticas
nos pontos 1 e 2
2
cilindro maciço
2
MvCM
1
4
3
v 
2
MR 2  CM   MvCM
4
 R 

1
2
2/3 translação
K1  U1  K 2  U 2
0  Mgh  Mv
3
4
2
CM
0
vCM 
4
gh
3
2
MvCM
1/3 rotação
Menor que a velocidade de um objeto
que cai de uma altura h
1
3
U K


2 gh .
Velocidade de um ioiô primitivo
Considerando o mesmo ioiô primitivo, agora calcule a aceleração de cima para baixo do
cilindro e a tensão no fio.
vCM 
R
4
gh
3

2
2
vCM

v
,f
CM ,i  2aCM YCM , f  YCM , i

2

T
 4 
gh   0  2aCM h


 3 
2
aCM  g
3
F
y
 Mg  (T )  Ma
2 
Mg  T  M  g 
3 
2
T  Mg  Mg
3
1
T  Mg
3
Velocidade de um ioiô primitivo
Considerando o mesmo ioiô primitivo, agora calcule a aceleração de cima para baixo do
cilindro e a tensão no fio.
R
Outra forma de resolução
F
y

T
 Mg  (T )  Ma
Somente a força de tensão possui torque em relação
ao eixo que passa pelo centro de massa, de modo que
a equação para o movimento de rotação em torno
desse eixo é:

 z  TR  I cm z 
1
MR 2 z
2
EX: Esfera Descendo Rolando por um plano inclinado
Se o corpo na Figura ao lado é uma esfera cheia, (a) Calcule a velocidade do seu centro de
massa na base do plano inclinado e (b) determine o módulo da aceleração translacional do
centro de massa.
(a) Considere a Terra e a esfera
como um corpo isolado e
usaremos o modelo de energia
(b)
Ki  U i  K f  U f
1
1
2
0  Mgh   MvCM

I CM  2 f )  0
,f
2
2
Sabendo que
vCM   R
temos que:
2
v
1
1
2
CM
,f
2
2
Mgh  MvCM

(
MR
)
,f
2
2 5
R2
1
1
2
2
 MvCM , f  MvCM
,f
2
5
7
10
2
 MvCM

v

gh
,f
CM , f
10
7

2
2
vCM
, f  vCM ,i  2aCM X CM , f  X CM ,i
aCM 
2
2
vCM

v
,f
CM ,i
2( X CM , f  X CM ,i )
10
gh  0
5
 7
 gsen
h
2(
) 7
sen

EX: Esfera Descendo Rolando por um plano inclinado
Se o corpo na Figura ao lado é uma esfera cheia, (a) Calcule a velocidade do seu centro de
massa na base do plano inclinado e (b) determine o módulo da aceleração translacional do
centro de massa.
(a)







Fx  Mg sin( )  ( f )  Macmx
z
(b)
2

 fR  I cm z   MR 2  z
5

2
2

fR   MR 2   z  MRacm
5
5

5
aCM  gsen
7
2
f  gsen
7
A força de atrito a ser considerada é estático.

2
2
vCM

v
,f
CM ,i  2aCM X CM , f  X CM ,i
5
 0  2 gsen (h)
7
10
vCM , f 
gh
7

EX: Momento angular em uma ação policial
Uma porta de largura L=1,0m e massa m=15 kg, é articulada com dobradiças em um dos
dois lados de modo que possa girar sem atrito em torno de um eixo vertical. Ela
inicialmente não está aberta. Um policial dá um tiro com uma bala de 10 g e velocidade de
400 m/s exatamente no centro da porta e em uma direção perpendicular ao plano da
porta. Calcule a velocidade angular da porta imediatamente depois que a bala penetra. A
energia cinética se conserva?
a ) L  mvr  I  Lembrando que:L=r  mv
Li  L f
I bi  ( I b  I p ) f
L
mb vi  ( I b  I p ) f
2
mb vi L
f 
2( I b  I p )
I b  MR 2  M ( L / 2)2
 (0, 01kg )(1m / 2)2  0, 0025kg.m2
(0, 01kg )(400m / s)(1m)
f 
2[(0, 0025kg.m 2 )  (5, 0kg.m 2 )]
 f  0, 4rad / s
Antes
ω
Depois
1
1
2
I p  ML  (15kg )(1m)2  5,0kg.m2
3
3
EX: Momento angular em uma ação policial
Uma porta de largura L=1,0m e massa m=15 kg, é articulada com dobradiças em um dos
dois lados de modo que possa girar sem atrito em torno de um eixo vertical. Ela
inicialmente não está aberta. Um policial dá um tiro com uma bala de 10 g e velocidade de
400 m/s exatamente no centro da porta e em uma direção perpendicular ao plano da
porta. Calcule a velocidade angular da porta imediatamente depois que a bala penetra. A
energia cinética se conserva?
b)
1
1
mb vi 2  (0, 01kg )(400m / s ) 2  800 J
2
2
1
1
K f  ( I b  I p ) f 2  (5, 0025kg.m 2 )(0, 4rad / s) 2  0, 4 J
2
2
Ki 
Não, a energia não se conserva.
Antes
ω
Depois
EX: Momento angular em uma ação policial
Um cilindro com momento de inércia I1 gira ao redor de um eixo vertical sem atrito com
velocidade angular ωi. Um segundo cilindro que tem momento de inércia I2 e não está
girando inicialmente, cai sobre o primeiro cilindro. Devido ao atrito entre as superfícies, os
dois cilindros atingem finalmente a mesma velocidade angular ωf. a) Calcule ωf. b) Mostre
que a energia cinética do sistema diminui nessa interação e calcule a razão da energia
rotacional final para a energia rotacional inicial.
a ) Li  L f
I11  ( I1  I 2 ) f
f 
I11
( I1  I 2 )
b) K i 
1
I1i 2
2
( I11 ) 2
1
1
2
K f  ( I1  I 2 ) f  ( I1  I 2 )
2
2
( I1  I 2 ) 2
1 ( I11 ) 2

2 I1  I 2
1 ( I11 ) 2
Kf
2 I1  I 2
I1


1
Ki
I1  I 2
I1i 2
2
MOVIMENTO DE PRECESSÃO, Ex:
– O MOVIMENTO PRECESSÃO é o
movimento do eixo de
simetria sobre o eixo vertical
(eixo z, no caso), descrevendo
um cone.
• O pião cairia se não estivesse girando.
• A regra da mão direito indica que :
 = r  F = r  M g no plano XY
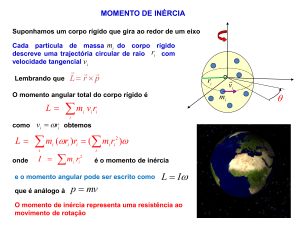
MOVIMENTO DE PRECESSÃO, Ex:
• Como está girando, tem um momento
angular. A direção do Momento Angular L
está ao longo do eixo de simetria
• O movimento do eixo de simetria ao redor
do eixo z (o mov. de Precessão) ocorre
devido ao torque produzir uma mudança
na direção do eixo de simetria.
• FORÇA GRAVITACIONAL M g produz o
toque ao redor de O.
• A regra da mão direito indica que :
 = r  F = r  M g no plano XY
O TORQUE RESULTANTE E O MOMENTO ANGULAR
DO PIÃO ESTÃO RELACIONADOS PELA:
dL
  dt
MOVIMENTO DE PRECESSÃO
– O MOVIMENTO PRECESSÃO é o movimento do eixo
de simetria sobre o eixo vertical
– O MOVIMENTO DE PRECESSÃO é geralmente lento
em relação ao movimento de rotação da parte
superior
– http://www.youtube.com/watch?v=sA3hLpSwL
ws 4.55 min
– http://www.youtube.com/watch?v=dW3OpgD
AQU8
MOVIMENTO DE PRECESSÃO
(a) Um giroscópio parado cai enquanto gira em torno do plano xz
por causa do Torque ().
  Mgrsen90  Mgr
o
(b) Um giroscópio que está girando com um momento angular
L executa um momento de precessão no plano xz em torno do
eixo z.
(c) A variação com o tempo do momento angular dL/dt, faz L
girar em torno de O.
dL   dt  Mgrdt
dL Mgrdt
d 

L
I
Mgr
  d / dt   
I
VELOCIDADE DE PRECESSÃO
Bibliografia
Serway, R. A.; Jewett Jr., J. W. Princípios de Física Mecânica Clássica, Vol. 1, cap. 10, Cengage Learning, 2004.
Young, H. D.; Freedman, R. A. Sears & Zemansky, Física I Mecânica, vol. 1, cap. 8, Pearson Education do Brasil, 2008.