FCM0101 Física 1 - 9 a lista de exercícios

FCM0101 Física 1 - 9a lista de exercícios
Entrega: 17/06/2015
1) Você está projetando um torno mecânico, parte do qual consiste em um cilindro
uniforme de 90 kg de massa e 0,40 m de raio, montado de forma a girar sem atrito em
torno de seu eixo. O cilindro é acionado por uma correia que o envolve em seu
perímetro e exerce um torque constante. Em t = 0, a velocidade angular do cilindro é
zero. Em t = 25 s, sua rapidez angular é 500 rev/min. (a) Qual é a magnitude da
quantidade de movimento angular do cilindro em t = 25 s? (b) Com que taxa está
aumentando a quantidade de movimento angular? (c) Qual a magnitude do torque
sobre o cilindro? (d) Qual a magnitude da força de atrito que atua sobre o perímetro
do cilindro?
2) Dois discos de mesma massa e raios diferentes (r e 2r) giram em torno de um eixo sem
atrito, com a mesma rapidez angular ω0 mas em sentidos opostos (ver figura a seguir).
Os dois discos são lentamente aproximados. A força de atrito entre as superfícies faz
com que eles passem a ter a mesma velocidade angular. (a) Qual é a magnitude
angular final, em termos de ω0? (b) Qual é a variação da energia cinética de rotação do
sistema? Explique.
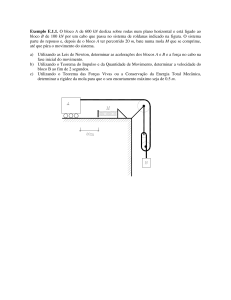
3) Uma barra uniforme, de comprimento L1 e massa M igual a 0,75 kg, está presa a uma
dobradiça de massa desprezível em uma das extremidades e é livre para girar no plano
vertical (ver figura a seguir). A barra é largada do repouso na posição mostrada. Uma
partícula de massa m = 0,50 kg, está suspensa da dobradiça por um fio fino de
comprimento L2. A partícula gruda na barra quando as duas encostam. Qual deve ser a
razão L2/L1 para que θmáx = 60o após a colisão?
4) Uma roda de bicicleta, de raio igual a 28 cm, etá montada no meio de um eixo de 50
cm de comprimento. O pneu e o aro pesam 30 N. A roda é posta a girar a 12 rev/s,
quando o eixo é colocado em posição horizontal com uma das extremidades apoiadas
em um pivô. (a) Qual a quantidade de movimento angular associado ao giro da roda?
(Trate a roda como um aro.) (b) Qual a velocidade angular de precessão? (c) Quanto
tempo leva para o eixo girar em torno do pivô varrendo 360o? (d) Qual é a quantidade
de movemento angular associada ao movimento do centro de massa, isto é, à
precessão? Qual é a sua orientação?
5) Uma barra fina e homogênea, de massa M, é suspensa horizontalmente por dois fios
verticais. Um dos fios prende-se à extremidade esquerda da barra, e o outro fio dista
2/3 do comprimento da barra, de sua extremidade esquerda. (a) Determine a tração
em cada fio. (b) Um objeto é, agora, pendurado por um cordão preso à extremidade
direita da barra. Quando isto acontece, percebe-se que a barra se mantém na
horizontal, mas a tração no fio da esquerda desaparece. Determine a massa do objeto.
6) Uma prancha gravitacional é uma maneira conveniente e rápida de se determinar a
localização do centro de gravidade de uma pessoa. Ela consiste em uma prancha
horizontal suportada por um fulcro em uma extremidade e uma balança de mola na
outra. Para uma demonstração em aula, seu professor de física pede que você deite
sobre a prancha com o topo de sua cabeça exatamente sobre o fulcro, como mostrado
na figura a seguir. O fulcro está a 2,00 m da balança. Preparando este experimento,
você se pesou previamente, com precisão, e verificou que sua massa é de 70,0 kg.
Quando você está sobre a prancha gravitacional, o ponteiro da balança adianta 250 N
além do ponto que indicava quando só a prancha estava sobre ela. Use estes dados
para determinar a localização de seu centro de massa em relação a seus pés.
7) Uma bola de 0,50 kg é presa a uma extremidade de um fio de alumínio que tem um
diâmetro de 1,6 mm e um comprimento não distendido de 0,70 m. A outra
extremidade do fio está fixa em cima de um poste. A bola gira em torno do poste em
um plano horizontal com uma rapidez rotacional tal que o ângulo entre o fio e a
horizontal é de 5o. Determine a tração no fio e o consequente aumento de seu
comprimento.
8) Duas esferas maciças e polidas (sem atrito), de raio r, são colocadas dentro de um
cilindro de raio R, como na figura a seguir. A massa de cada esfera é m. Determine a
força exercida pela base do cilindro sobre a esfera de baixo, a força exercida pela
parede do cilindro sobre cada esfera e a força exercida por uma esfera sobre a outra.
Expresse todas as forces em termos de m, R e r.