Semelhança de figuras e semelhança de triângulos

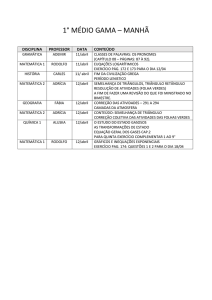
Escola Secundária com 3º Ciclo do Ensino Básico de Lousada
PM
Ano lectivo: 2008/2009
Ficha de Trabalho de Matemática nº16
Tema: Semelhança de Figuras. Semelhança de Triângulos. (Revisões)
Nome: __________________________________________________________
Data: ______________
Nº ____ Turma _____
Figuras Semelhantes
Recorda:
Dois polígonos são semelhantes quando os ângulos correspondentes são geometricamente iguais
e os lados correspondentes directamente proporcionais.
Nota: A definição de polígonos semelhantes só é válida quando ambas as condições são satisfeitas: ângulos
correspondentes geoemetricamente iguais e lados correspondentes directamente proporcionais. Apenas uma das
condições não é suficiente para indicar a semelhança entre polígonos.
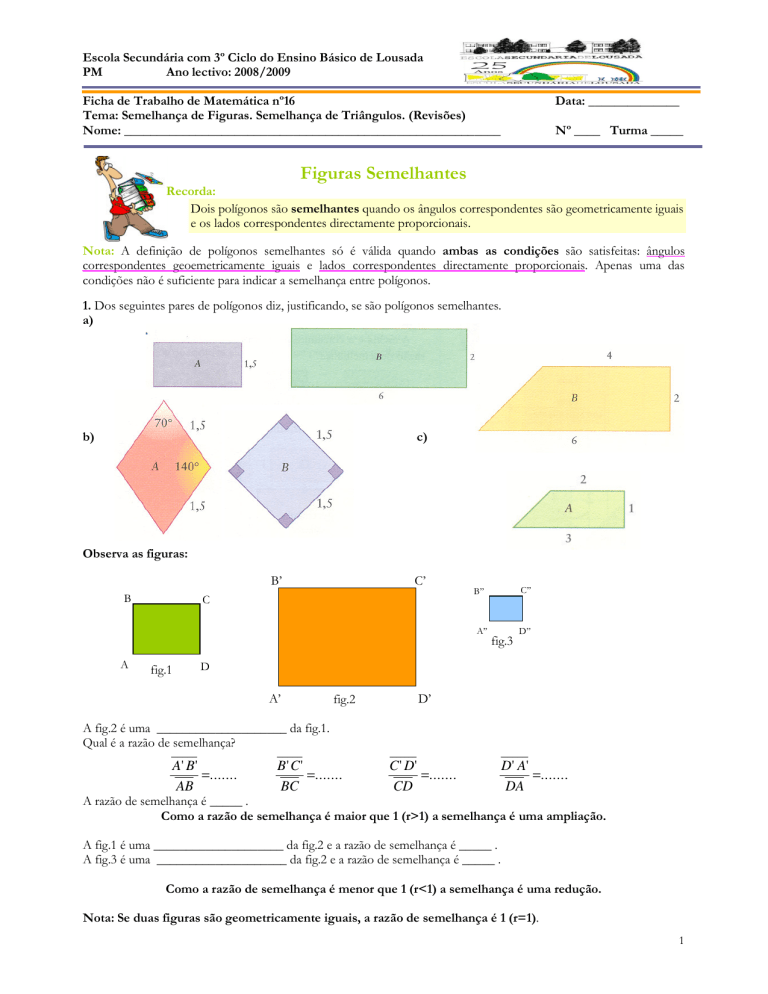
1. Dos seguintes pares de polígonos diz, justificando, se são polígonos semelhantes.
a)
b)
c)
Observa as figuras:
B’
B
C’
C
A’’
A
fig.1
C’’
B’’
fig.3
D’’
D
A’
fig.2
D’
A fig.2 é uma ____________________ da fig.1.
Qual é a razão de semelhança?
A' B '
=.......
AB
B' C'
=.......
BC
C ' D'
=.......
CD
D' A'
=.......
DA
A razão de semelhança é _____ .
Como a razão de semelhança é maior que 1 (r>1) a semelhança é uma ampliação.
A fig.1 é uma ____________________ da fig.2 e a razão de semelhança é _____ .
A fig.3 é uma ____________________ da fig.2 e a razão de semelhança é _____ .
Como a razão de semelhança é menor que 1 (r<1) a semelhança é uma redução.
Nota: Se duas figuras são geometricamente iguais, a razão de semelhança é 1 (r=1).
1
2. Determina as dimensões dos polígonos semelhantes aos dados de acordo com a razão de proporcionalidade.
b) r = 3
a) r = 2
5
c) r = 1,5
3. A e B são pentágonos regulares e semelhantes. O pentágono A tem de perímetro 11 cm. O pentágono B tem 11 cm
de lado. B é uma ampliação de A. Porquê?
4. Proporcionalidade entre lados correspondentes
a) Os rectângulos A e B são semelhantes. Calcula x.
b) Os trapézios A e B são semelhantes. Calcula x e y.
Triângulos Semelhantes
No 7ºano utilizaste a semelhança de triângulos para resolver alguns problemas
de distâncias relativas a pontos inacessíveis. Aprendeste que para assegurar a
semelhança de dois triângulos não é necessário verificar se têm de um para o
outro os ângulos geometricamente iguais e todos os lados directamente
proporcionais. É suficiente, verificar se têm, de um para o outro, dois pares
de ângulos geometricamente iguais.
5. Na figura o ângulo ABC tem a mesma amplitude que o ângulo
DFE.
a) Porque é que as velas são semelhantes?
b) Se BC = 4 m calcula EF .
6. Observa a figura.
a) Mostra que os triângulos [FGH] e [JKL] são semelhantes.
b)Determina o comprimento do lado do triângulo
correspondente ao lado [GH], com aproximação às décimas.
[JKL],
2
7. Observa a figura.
7.1. Calcula:
^
b) A D C
a) BÂD
^
d) A C B
c) DÂC
7.2. Os triângulos [ABD], [ABC] e [ADC] são semelhantes. Porquê?
8. Observa a figura e determina, a altura da árvore sabendo que o
António mede 1,5 m.
9. Observa a figura:
9.1. Mostra, justificando convenientemente, que os triângulos [ABC] e [CDE] são semelhantes.
9.2. Sabendo que AB =18 cm , DE =24 cm e CE =32 cm, determina BC .
Para descobrir…
10. O triângulo [ABC] é rectângulo em A e [AH] é a altura referente à hipotenusa.
10.1. Justifica as afirmações:
^
^
^
a) A H C = A H B = B AC ;
^
^
^
b) A B C = 90º − AC B ;
^
c) C A H = 90º − A C B ;
d) O triângulo [AHC] é semelhante ao triângulo [ABC];
e) O triângulo [AHB] é semelhante ao triângulo [ABC];
f) O triângulo [AHC] é semelhante ao triângulo [AHB].
10.2. Assim, podemos concluir que:
Num triângulo rectângulo, a altura referente à hipotenusa divide-o em ________ triângulos
rectângulos ____________________ entre si e _____________________ ao triângulo dado.
3
11. Calcula o valor de x:
12. Um insecto parte do ponto M e percorre os segmentos [MA] e [AC],
parando no ponto C. Um outro insecto parte do ponto C e percorre os
segmentos [CB] e [BM], parando no ponto M.
a) Prova que os triângulos [AMC] e [CMB] são semelhantes.
b) Determina:
1º) a distância que separa os dois insectos;
2º) a distância percorrida pelo primeiro insecto.
4