Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
CAPÍTULO 28 – O CAMPO ELÉTRICO
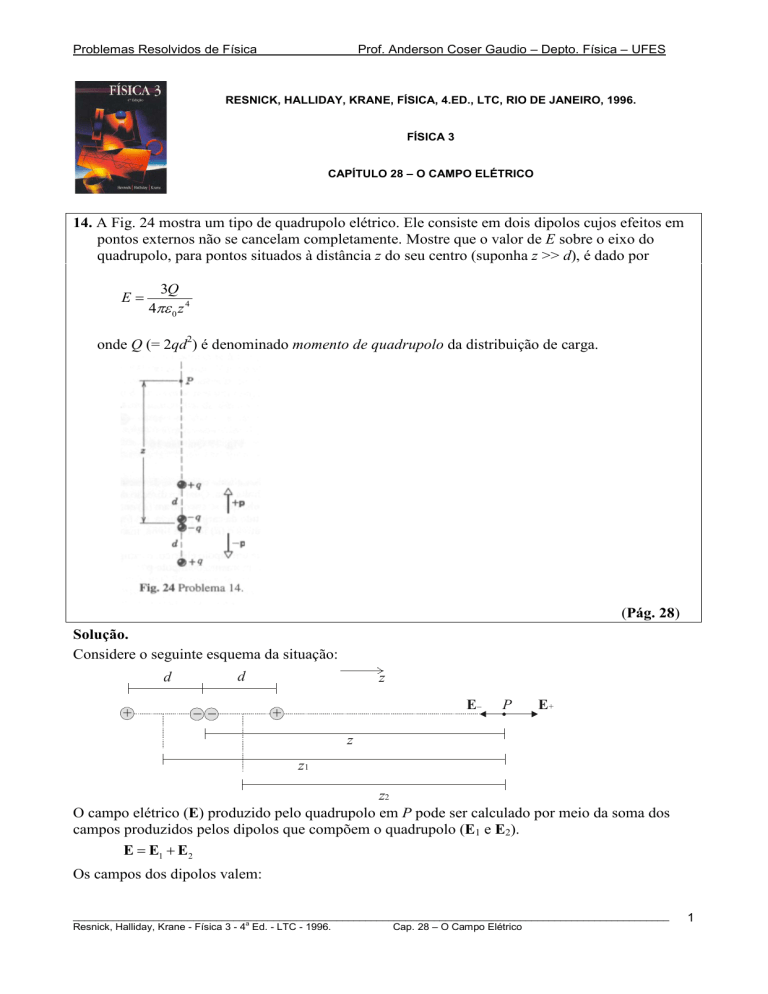
14. A Fig. 24 mostra um tipo de quadrupolo elétrico. Ele consiste em dois dipolos cujos efeitos em
pontos externos não se cancelam completamente. Mostre que o valor de E sobre o eixo do
quadrupolo, para pontos situados à distância z do seu centro (suponha z >> d), é dado por
E=
3Q
4πε 0 z 4
onde Q (= 2qd2) é denominado momento de quadrupolo da distribuição de carga.
(Pág. 28)
Solução.
Considere o seguinte esquema da situação:
d
d
+
−−
z
E−
+
P
E+
z
z1
z2
O campo elétrico (E) produzido pelo quadrupolo em P pode ser calculado por meio da soma dos
campos produzidos pelos dipolos que compõem o quadrupolo (E1 e E2).
E
= E1 + E2
Os campos dos dipolos valem:
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 28 – O Campo Elétrico
1
Problemas Resolvidos de Física
E1 = −
E2 =
Prof. Anderson Coser Gaudio – Depto. Física – UFES
1 2qd
i
4πε 0 z13
1 2qd
i
4πε 0 z23
Sendo que as distâncias z1 e z2 são definidas por:
d
z1= z +
2
d
z 2= z −
2
O módulo do campo E vale:




2qd 
1
1

E
=
−
3
3


4πε 0 
d 
d
 z −   z +  
2 
2 

Multiplicando-se e dividindo-se o segundo membro desta equação por z3, teremos:
2qd
E
=
4πε 0 z 3
−3
−3

d 
d  

 1 −  −  1 +  
 2 z  
 2 z 
Aplicando-se a expansão binomial (Apêndice H, pág. A-288) e omitindo-se os termos de ordem
superior (z >> d):
=
E
2qd  3d
  3d

+   − 1 −
+ 
1+
3 
4πε 0 z  2 z
  2z

E
=
2qd 3d 3.2qd 2
3Q
=
=
3
4
4πε 0 z z
4πε 0 z
4πε 0 z 4
Em notação vetorial:
3Q
E=
i
4πε 0 z 4
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 28 – O Campo Elétrico
2