Integral definido

Matemática - 2008/09 - Integral de…nido
68
Integral de…nido
Introdução
Seja f uma função real de variável real de…nida e contínua num intervalo real I = [a; b]
e tal que f (x)
0; 8x 2 [a; b]: Se dividirmos [a; b] em n intervalos iguais, a amplitude
b a
: Designando por x0 ; x1 ; : : : ; xn os extremos consecutivos
h de cada um deles é h =
n
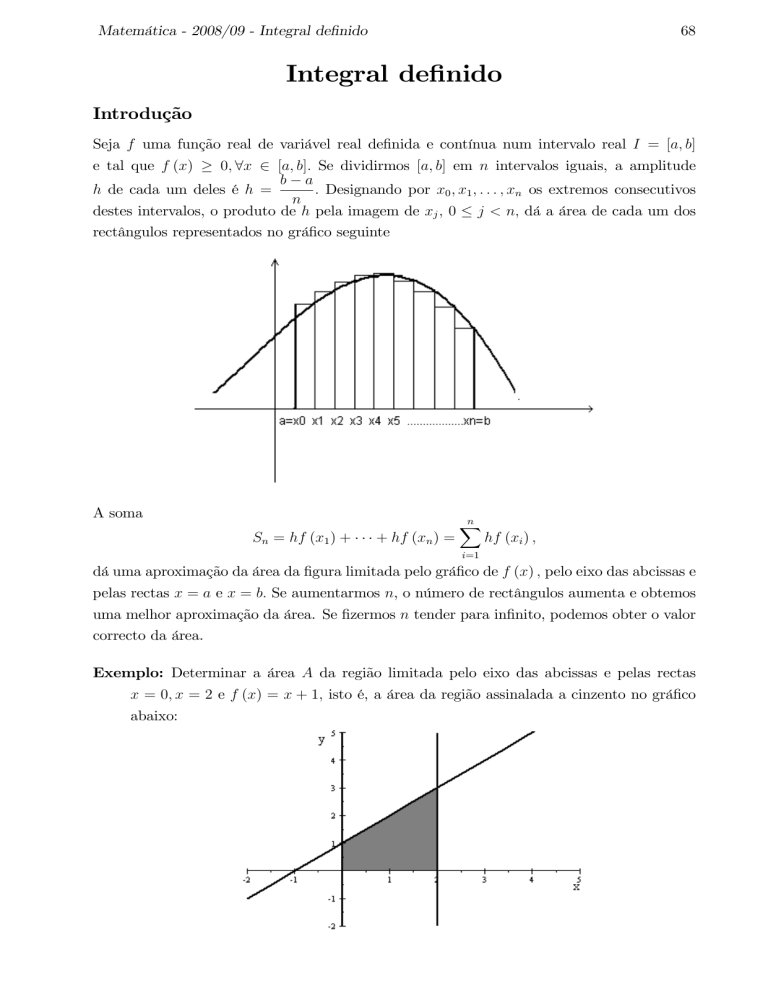
destes intervalos, o produto de h pela imagem de xj ; 0 j < n; dá a área de cada um dos
rectângulos representados no grá…co seguinte
A soma
Sn = hf (x1 ) +
+ hf (xn ) =
n
X
hf (xi ) ;
i=1
dá uma aproximação da área da …gura limitada pelo grá…co de f (x) ; pelo eixo das abcissas e
pelas rectas x = a e x = b: Se aumentarmos n, o número de rectângulos aumenta e obtemos
uma melhor aproximação da área. Se …zermos n tender para in…nito, podemos obter o valor
correcto da área.
Exemplo: Determinar a área A da região limitada pelo eixo das abcissas e pelas rectas
x = 0; x = 2 e f (x) = x + 1; isto é, a área da região assinalada a cinzento no grá…co
abaixo:
Matemática - 2008/09 - Integral de…nido
69
Seguindo o que foi referido atrás, divide-se o intervalo [0; 2] em n intervalos iguais e
tem-se:
2
4
2n
; x2 = ; : : : ; x n =
= 2;
n
n
n
2i
+ 1;
para cada xi; f (xi ) = xi + 1 =
n
2
a amplitude de cada intervalo é h =
n
x0 = 0; x1 =
Assim, para este caso
2 X 2i
2
Sn =
+1=
n i=1 n
n
n
Então A = lim Sn = lim 2
!
n
n
X
2X
2
i+
1 =
n i=1
n
i=1
2 n (n + 1)
+n
n
2
=2
n+1
+2
n
n+1
+2=4
n
Este método não parece muito e…caz para o cálculo de áreas. O exemplo apresentado é
um caso muito simples, (que não necessitava de este tipo de cálculo, dado tratar-se de uma
área facilmente calculável por uma simples decomposição da …gura num triângulo e num
rectângulo) e mesmo assim deu algum trabalho. No entanto o procedimento apresentado
generaliza-se e conduz à de…nição de integral de…nido.
Integral de…nido
Seja f uma função contínua num intervalo real I = [a; b]. O raciocínio feito anteriormente
pode ser feito de forma mais geral, dividindo [a; b] em n intervalos não regulares [xi ; xi+1 ] de
amplitude hi e escolhendo, não um dos extremos do intervalo, mas um qualquer valor xi do
intervalo [xi ; xi+1 ]. A soma obtida seria então
n
X
hi f (xi ) :
i=1
A partir daqui obtém-se a de…nição de integral de…nido:
De…nição Chama-se integral de…nido de f no intervalo [a; b] ao limite, se existir, de
n
X
hi f (xi ) ;
i=1
quando hi ! 0:
O integral, tal como foi de…nido (e quando existe...) representa-se por
Zb
a
f (x) dx;
Matemática - 2008/09 - Integral de…nido
70
que se lê integral (relativo a x) de f (x) entre a e b e diz-se que a função é integrável no
intervalo [a; b] : A função f é a função integranda, x a variável de integração e a e b os
limites de integração.
Pode-se colocar a questão de quais são as funções integráveis num determinado intervalo
[a; b] : O seguinte teorema caracteriza muitas dessas funções:
Teorema 1 Se f é uma função contínua num intervalo [a; b] ; então f é integrável em [a; b] ;
Rb
isto é , existe f (x) dx:
a
Note-se que o teorema diz apenas que uma função contínua é integrável, não diz que se não
fôr contínua não é integrável.
Propriedades
A de…nição de integral permite inferir uma série de propriedades para funções integráveis
num intervalo [a; b]:
Propriedades:
1. Sendo k 2 R,
2.
Ra
Rb
kdx = k (b
a) :
a
f (x) dx = 0:
a
3.
Rb
Ra
f (x) dx =
a
4.
Rb
f (x) dx:
b
(f (x) + g (x)) dx =
a
5. Sendo k 2 R,
Rb
f (x) dx +
a
Rb
Rb
g (x) dx:
a
kf (x) dx = k
a
Rb
f (x) dx:
a
6. Se f é contínua em [a; b] e a < c < b; então
Zb
f (x) dx =
a
7. Se 8x 2 [a; b] ; f (x)
8. Se 8x 2 [a; b] ; m
Zc
f (x) dx +
a
g (x), então
Rb
Rc
f (x) dx
M , então m (b
f (x) dx:
c
a
f (x)
Zb
g (x) dx
a
a)
Rb
a
f (x) dx
M (b
a) :
Matemática - 2008/09 - Integral de…nido
71
Teorema fundamental do cálculo integral
O teorema fundamental do cálculo integral permite o cálculo de integrais de…nidos sem
recorrer à de…nição e mostra a relação entre integrais de…nidos e primitivas (ou integrais
inde…nidos).
Teorema 2 (Teorema fundamental do cálculo integral) Seja f uma função contínua
num intervalo real I = [a; b] e ' (x) a função de…nida, 8x 2 [a; b]; por
' (x) =
Zx
f (t) dt:
a
Então '0 (x) = f (x) :
Corolário Se f é uma função contínua num intervalo real I = [a; b] e F é uma primitiva de
f em [a; b]; então
Zb
f (x) dx = F (b)
F (a) :
a
Demostração (do corolário) Seja F uma primitiva de f em [a; b]: Como F (x) e
Zx
' (x) = f (x) dx são primitivas da mesma função, diferem apenas numa constante,
isto é,
a
Zx
f (x) dx = F (x) + k:
a
Para x = a; vem
Za
f (x) dx = F (a) + k ,
a
, 0 = F (a) + k
, k=
F (a)
Para x = b; tem-se
Zb
f (x) dx = F (b) + k:
a
Substituindo k por
F (a) obtém-se, então,
Zb
f (x) dx = F (b)
F (a)
a
Observação: A diferença F (b)
[F (x)]ba = F (b)
F (a) costuma representar-se por [F (x)]ba e à igualdade
F (a) chama-se fórmula de Barrow.
Matemática - 2008/09 - Integral de…nido
72
Exemplos:
Z17
1. 4 dx = [4x]17
5 = 4 (17
5) = 48
5
2.
Z5
ex dx = [ex ]51 = e5
Z5
x2 dx =
e
1
3.
5
x3
3
=
1
1
4.
Z5
x3
3
x2 dx =
1
5.
Z2
(x
2) dx ==
53
3
13
124
=
3
3
5
=
1
( 5)3
3
2
x2
2
2x
=
0
0
6.
Z4
x2
2) dx =
2
(x
4
2x
2
2
7.
Z1
( x
2
( 1)3
=
3
42
=
2
2
2
1
3
=
2
1
+2
2
1
3
2
( 2)
3
1
22
2
4
8.
1
dx = [ln x]e1 = ln e
x
9.
Z2
sin x dx = [ cos x]20 =
10.
Z
sin x dx = [ cos x]0 =
11.
Z2
( sin x) dx = [cos x]2 = cos (2 )
12.
Zx
t3
t dt =
3
0
2
2
( 2))
!
=
2
=2
=
( 2)
+ (2
2
Ze
2
2
2
3
02
2
2
x2
+ 2x
2
x3
3
x + 2) dx: =
22
2
124
3
=
9
2
ln 1 = 1
1
cos (2 )
( cos (0)) =
1+1=0
0
cos ( )
( cos (0)) = 1 + 1 = 2
0
x
2
1
13. Se ' (x) =
Zx
=
1
x3
3
(cos ) = 1
( 1) = 2
1
3
t2 dt, pelo teorema fundamental do cálculo integral, '0 (x) = x2 : Isto
1
pode ser con…rmado derivando directamente a expressão obtida no exemplo 3.
Zx 2
t
x2
0
14. Se ' (x) =
dt,
aplicando
o
teorema
fundamental,
'
(x)
=
:
t2 + 1
x2 + 1
1
Matemática - 2008/09 - Integral de…nido
73
Aplicações do integral de…nido ao cálculo de áreas
O integral de…nido tem aplicações directas ao cálculo de áreas. Consideramos, no que se
segue, funções contínuas num intervalo [a; b] :
Caso 1: Se f (x)
0; 8x 2 I; então a área A da …gura delimitada pelo grá…co de f (x),
pelo eixo das abcissas e pelas rectas x = a e x = b é
A=
Zb
f (x) dx
a
Exemplo:
1
; calcular a área A da …gura delimitada pelo grá…co de f (x), pelo
x
eixo das abcissas e pelas rectas x = 1 e x = e; ou seja, a área assinalada a cinzento no
Sendo f (x) =
grá…co abaixo:
Como no intervalo [1; e] se tem f (x)
A=
Ze
0;
1
dx = [ln x]e1 = ln e
x
ln 1 = 1
1
Caso 2: Se f (x)
0; 8x 2 I; então a área da …gura descrita atrás é dada pelo simétrico do
integral (evidentemente que uma área não pode ser negativa).
A=
Zb
f (x) dx
a
Exemplo: Sendo f (x) = x2
5x + 4; calcular a área A da …gura delimitada pelo grá…co de
f (x), pelo eixo das abcissas e pelas rectas x = 2 e x = 4; ou seja, a área assinalada a
Matemática - 2008/09 - Integral de…nido
74
cinzento no grá…co abaixo:
No intervalo [2; 4], f (x)
A =
Z4
x
2
0 pelo que
5x + 4 dx =
x3
3
5x2
+ 4x
2
23
3
5
2
=
43
3
42
5
2
+4
4
22
2
4
=
2
+4
2
=
10
3
=
10
3
Caso 3: Quando a função toma valores positivos e negativos no intervalo [a; b] o integral
não dá directamente a área, podendo tomar valores negativos ou nulos. Por exemplo,
o integral da função sin x entre 0 e 2 é 0; como foi visto no exemplo 9 da página 72:
De facto, observando o grá…co de sin x;
vê-se que as áreas das regiões a cinzento assinaladas por A1 e A2 são iguais e, por isso,
os valores do integral de sin x entre 0 e
e entre
e 2 são simétricos e anulam-se.
No entanto a área A = A1 + A2 não é 0!
Então, para funções que tomem valores negativos e positivos num intervalo [a; b], a área
A da região delimitada pelo grá…co da função, pelo eixo das abcissas e pelas rectas
Matemática - 2008/09 - Integral de…nido
75
x = a e x = b é dada por
A=
Zb
jf (x)j dx:
a
No exemplo anterior a área da …gura assinalada a cinzento, é dada por
Z2
jsin xj dx:
0
Como sin x
0 entre 0 e e sin x 0 entre e 2 ; tem-se
Z2
Z
Z2
jsin xj dx = sin x dx + ( sin x) dx = 2 + 2 = 4
0
0
O cálculo dos dois últimos integrais foi feito nos exemplos 10 e 11 da página 72.
Caso 4: É ainda possível calcular as áreas de regiões delimitadas por duas funções, para o
que se tem:
1. Se f e g são funções contínuas tais que f (x)
g (x) ; 8x 2 [a; b], a área A da região
limitada pelas funções f (x) e g (x) e pelas rectas x = a e x = b é
A=
Zb
(f (x)
g (x)) dx
a
Exemplo: Vamos determinar a área A da região do plano delimitada pelos grá…cos
x2 e g (x) = x
das funções f (x) =
2. Esboçando o grá…co vê-se que se pretende
determinar a área assinalada a cinzento no grá…co seguinte:
Neste caso, para determinar os limites de integração resolve-se a equação
a…m de determinar as abcissas dos pontos de intersecção dos dois grá…cos:
x2 = x
Assim
A=
Z1
2
(f (x)
2 , x = 1 ou x =
g (x)) dx =
Z1
x2
(x
2:
2) dx =
2
O cálculo do último integral foi feito no exemplo 7 da página 72.
9
2
x2 = x
2;
Matemática - 2008/09 - Integral de…nido
76
2. Se f e g são funções contínuas quaisquer no intervalo [a; b] ; a área A da região limitada
pelas funções f (x) e g (x) e pelas rectas x = a e x = b é
A=
Zb
jf (x)
g (x)j dx
a
Exemplo: Vamos determinar a área A da região do plano delimitada pelos grá…cos
3
5
das funções f (x) = sin x e g (x) = cos x e pelas rectas x =
e x =
; que
4
4
corresponde à região assinalada a cinzento no seguinte grá…co:
Veri…ca-se que, entre
neste caso, A =
Z
5
4
3
e ; sin x
4
4
jsin x
cos x e que, entre
4
e
5
sin x
4
cos x: Então,
cos xj dx; o que corresponde a calcular A1 + A2 :
3
4
5
A=
Z4
jsin x
cos xj dx =
3
4
Z4
(cos x
3
4
|
= [sin x + cos x] 4 3 + [ cos x
4
= sin +cos
4
4
p
p
2
2
=
+
2
2
5
sin
p
2
2
sin x) dx +
{z
}
A1
sin x]
5
4
=
Z4
|4
(sin x
cos x) dx =
{z
A2
}
4
3
3
+ cos
4
4
p ! p
p
2
2
2
+
+
2
2
2
+
5
5
sin
4
4
p
p !
p
2
2
=4 2
2
2
cos
cos
4
sin
4
=