Triângulos - matelementar

Triângulos
DEFINIÇÃO
Do latim - triangulu, é
um polígono de três lados
e três ângulos. Os três
ângulos de um triângulo
são designados por três
letras maiúsculas A, B e C
e os lados opostos a eles,
pelas mesmas três letras,
minúsculas a, b e c.
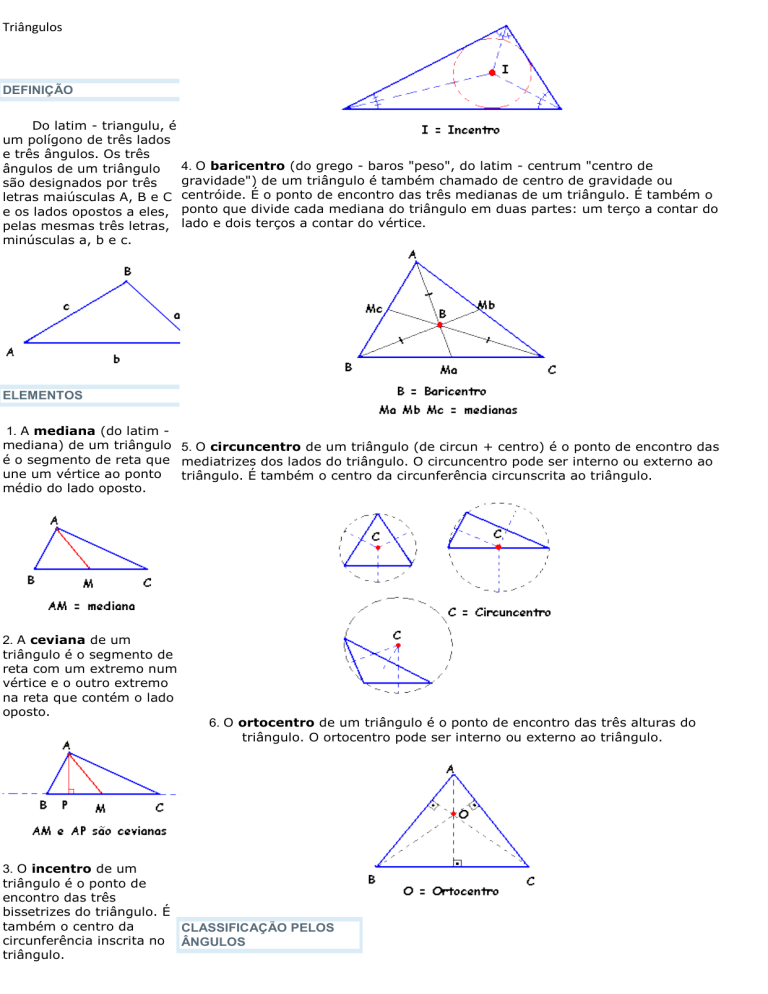
4. O baricentro (do grego - baros "peso", do latim - centrum "centro de
gravidade") de um triângulo é também chamado de centro de gravidade ou
centróide. É o ponto de encontro das três medianas de um triângulo. É também o
ponto que divide cada mediana do triângulo em duas partes: um terço a contar do
lado e dois terços a contar do vértice.
ELEMENTOS
1. A mediana (do latim mediana) de um triângulo 5. O circuncentro de um triângulo (de circun + centro) é o ponto de encontro das
é o segmento de reta que mediatrizes dos lados do triângulo. O circuncentro pode ser interno ou externo ao
une um vértice ao ponto
triângulo. É também o centro da circunferência circunscrita ao triângulo.
médio do lado oposto.
2. A ceviana de um
triângulo é o segmento de
reta com um extremo num
vértice e o outro extremo
na reta que contém o lado
oposto.
6. O ortocentro de um triângulo é o ponto de encontro das três alturas do
triângulo. O ortocentro pode ser interno ou externo ao triângulo.
3. O incentro de um
triângulo é o ponto de
encontro das três
bissetrizes do triângulo. É
também o centro da
CLASSIFICAÇÃO PELOS
circunferência inscrita no ÂNGULOS
triângulo.
1. Acutângulo é o
LADOS
triângulo que tem todos os
ângulos agudos.
1. Eqüilátero é o triângulo que possui seus três lados congruentes, ou seja,
iguais. Um triângulo eqüilátero também é um triângulo eqüiângulo
2. Eqüiângulo é o
triângulo que possui os
seus três ângulos
congruentes. Um triângulo
eqüiângulo também é um
triângulo eqüilátero.
2. Escaleno é o triângulo que não possui os seus tres lados congruentes.
3. Isósceles é o triângulo que possui dois lados e os dois ângulos adjacentes à
base congruentes.
3. Obtusângulo é o
triângulo que possui um
ângulo obtuso.
TRIÂNGULO INSCRITO EM
TRIÃNGULO
Ortico é um triângulo cujos vértices A'B'C' são os pontos resultantes da
interseção das alturas de um outro triângulo ABC com suas respectivas bases (pés
das alturas). Portanto ele se encontra inscrito dentro de um outro triângulo.
4. Retângulo é o triângulo
que possui um ângulo
reto. Veja a demonstração
do teorema de Pitágoras.
CLASSIFICAÇÃO PELOS
Atividade I : Assista ao video sobre triângulos.
http://tvescola.mec.gov.br/tve/video/mao-na-forma-dialogo-geometrico
Atividade II
1. Diga se é possível construir um triângulo com lados cujas medidas são:
a) a = 8 cm, b = 6 cm e c = 5 cm
b) a = 10 cm, b = 10 cm e c = 8 cm
c) a = 5 cm, b = 2 cm e c = 3 cm
d) a = 5,4 cm, b = 1 cm e c = 3,5 cm
e) a = 6,5 cm, b = 4,5 cm e c = 5 cm
2. Classifique os triângulos abaixo:
QUANTO AOS LADOS
(
) Equilátero
(
) Isósceles
(
) Escaleno
QUANTO AOS ÂNGULOS
(
) Acutângulo
(
(
QUANTO AOS LADOS
) Obtusângulo
) Retângulo
QUANTO AOS ÂNGULOS
(
) Equilátero
(
) Acutângulo
(
) Isósceles
(
) Obtusângulo
(
) Escaleno
(
) Retângulo
3. Determine o valor dos termos desconhecidos nos triângulos abaixo:
b)
a)
52º
85º
x
4x – 40º
x + 20º
x
c)
d)
60º
3x – 16º
4x + 22º
x
2x + 6º
26º
y
30º
4. Na figura abaixo. Determine os segmentos que representam, mediana, bissetriz
e altura, sabendo que BP = PC e BÂN = NÂC.
A
AH =
AN =
B
H
N
P
C

 
AP =
5. Na figura, med B̂ = 40º, med Ĉ = 60º. Se D é o incentro do triângulo ABC, então
x vale:
A
x
B
a) 40º
C
b) 120º
c) 130º
d) 150º
e) 100º
6. No triângulo ABC abaixo, AM é a mediana. Determine o perímetro desse triângulo.
A
3,5 cm
2,5 cm
B
1,9 cm
M
C
7. Na figura abaixo, AH é altura, calcule x e y:
A
x
30º
y
 
B
50º
C
H
8. Na figura abaixo, AD é bissetriz. Calcule a e b:
A
a
50º
30º
B
b
D
C
9. Determine o valor de x, sabendo que AD e BC são bissetrizes dos ângulos
E
indicados.
C
x
20°
B
A
10. Determine o valor de x de cada figura abaixo:
a)
40º
b)
130º
2x
x
3x
x
120º
11. Na congruência de triângulos, estudamos quatro casos, são eles: L.L.L.,
L.A.L.,
A.L.A. e L.A.AO. Indique o caso de congruência nos pares de triângulos abaixo:
a)
c)
5 cm
5 cm
50º
30º
3 cm
3 cm
3 cm
4 cm
3 cm
4 cm
b)
d)
3 cm
4cm
3 cm
100º
30º
100º
4 cm
4 cm
120º
30º
4 cm
120º
12. Quais os possíveis casos de congruência para o par de triângulos abaixo?
30º
30
30º
40º
40
40
30
40º
a) LLL; LAL; ALA
b) LAL; LAAo; LLL
c) LAAo; LAL; ALA
d) AA; LAL; LAAo
e) AA; LAAo; LLL
13. Na figura, o ABC é congruente ao EDC. Determine o caso de congruência e o valor de x e y.
15
23
3y +
2x – 3
2
QUADRILÁTEROS
Um quadrilátero é um polígono de quatro lados. Pode ser dito
que é porção do plano limitada por uma poligonal fechada,
A
B
Lados:
Vértices:
AB
BC
CD
AD
A
B
C
D
C
Diagonais:
AC
BD
D
Algumas Propriedades dos quadriláteros
1.
A soma dos seus ângulos internos é 360°.
2. A soma dos seus ângulos externos é 360°.
Classificação dos Quadriláteros
a) Paralelogramo
Chama-se paralelogramo o quadrilátero que possui lados paralelos dois a dois (lados opostos paralelos).
Propriedades dos Paralelogramos
•
•
Seus lados e seus ângulos opostos são congruentes.
Suas diagonais se cortam no ponto médio.
Classificação dos paralelogramos
1. No quadrado
•As diagonais são iguais e perpendiculares nos seus pontos médios.
•Todos os ângulos interno são retos.
•Seus lados são iguais.
QUADRADO
•O quadrado pose ser inscrito numa circunferência de raio igual a sua
semi diagonal.
No retângulo
• As diagonais são oblíquas, iguais e se cortam
nos seus pontos médios.
•Todos os ângulos interno são retos.
•Seus lados opostos são iguais.
RETÂNGULO
•O retângulo pose ser inscrito numa circunferência de raio igual a
sua metade da diagonal.
No losango
• As diagonais são diferentes, perpendiculares, se cortam nos seus
pontos médios e são bissetrizes dos ângulos internos.
•Nenhum ângulo interno é reto.
LOSANGO
•Seus lados são iguais.
•Não é inscritível.
No paralelogramo
• As diagonais são diferentes, oblíquas e se cortam nos seus pontos
médios.
•Nenhum ângulo interno é reto.
•Seus lados opostos são iguais.
PARALELOGRAMO
•Não é inscritível.
b) Trapézio
Chama-se trapézio o quadrilátero que possui somente dois lados opostos paralelos
e estes recebem a denominação de bases do trapézio.
Apresenta dois
ângulos de 90°
Trapézio Retângulo:
Os lados opostos não paralelos são congruentes
As diagonais são congruentes
Os ângulos de uma mesma base são congruentes
Trapézio Isósceles
Os lados opostos não
paralelos, não são
congruentes
Trapézio Escaleno
Atividade I: Assista o vídeo
sobre quadriláteros.
http://tvescola.mec.gov.br/tve/video/mao-na-forma-quadrado-cubo-e-cia
Atividade II
Desenhar um quadrado de
diagonal = 65 mm
Desenhar uma circunferência de diâmetro igual a
diagonal e inscrever o quadrado nesta
circunferência.
Desenhar um quadrado
de lado = 40 mm
Desenhar perpendiculares pelos extremos do lado
e sobre estas marcar o valor do lado. (não usar
esquadros nas construções).
Desenhar um quadrado sabendo
que a somo da diagonal e do lado
é igual a 55 mm
Desenhar um retângulo conhecendo
os dois lados, simultaneamente 40
mm e 20 mm.
C
A
B
•Desenhar quadrado de lado AB qualquer:
•Acrescentar, sobre a mesma reta suporte da
diagonal e a partir de seu extremo, o valor do lado
obtendo o ponto C:
•Unir o ponto C ao Ponto B:
•Marcar, a partir do ponto A e sobre a reta suporte
da diagonal, o valor 55 mm (diagonal + lado do
quadrado que se quer desenhar) obtendo o ponto
D;
•Pelo ponto D traçar uma paralela ao segmento BC
obtendo o ponto E;
•AE é o lado do quadrado proposto.
•Desenhar um dos lados, por exemplo AB, e por
um dos extremos levantar uma perpendicular;
•Sobre a perpendicular marcar o valor do outro
lado obtendo o ponto C;
•O segmento AC é o diâmetro da circunferência
que inscreve o retângulo.
Desenhar o losango de diagonal =
50 mm e lado = 30 mm
Desenhar o trapézio retângulo de
bases 50 e 20 mm, sabendo que sua
altura é 30 mm.
•Desenhar uma reta e sobre ela marcar 50 mm
(diagonal do losango;)
•Desenhar uma reta e sobre ela marcar 50 mm
(base maior);
•Centrar o compasso nos seus extremos e traçar
arcos de raio = 30 mm (lado do losango);
•Por um de seus extremos levantar uma
perpendicular de 30 mm (altura);
•As intersecções dos arcos são os dois outros
vértices do quadrilátero.
•Pelo extremo da perpendicular traçar uma paralela
a base;
•Sobre esta paralela marcar 20 mm (base menor).
Desenhar o trapézio isósceles com os seguintes
dados:
Base maior = 50 mm; Base menor = 30 mm e
Altura = 30 mm.
Desenhar uma reta e sobre ela marcar 50 mm (base maior);
•Por um de seus extremos levantar uma perpendicular de 30 mm (altura);
•Pelo extremo da perpendicular traçar uma paralela a base;
•Sobre esta paralela marcar 20 mm (base menor).
Foram apesentados alguns modelos que podem ser usados em sala de aula, com vídeos,
exercícios tradicionais e construção de figuras com instrumentos geométricos. Em grupo
produza um texto informando como vocês imaginam poder utilizar essas ferramentas na sua
prática profissional.