Torção em Eixos de Secção Circular • O gerador reage, exercendo

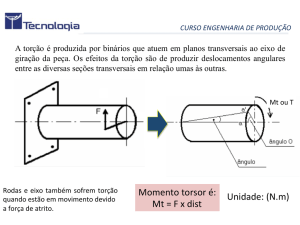
CURSO ENGENHARIA DE PRODUÇÃO Torção em Eixos de Secção Circular •  A turbina exerce sobre o eixo de
transmissão o momento torçor T.
•  O eixo transmite o momento T ao
gerador.
•  O gerador reage, exercendo sobre o
eixo um momento igual e contrário T’.
1 Power Transmission
A potência P transmi1da está relacionada com o torque T e a rotação ω através da relação: P = Tω
ω = 2πf
f = Hz ou rev/s
2 EXERCÍCIOS 3 CURSO ENGENHARIA DE PRODUÇÃO 1 tensão de cisalhamento t. ρ / J τ = M
Potência . ω
P=T
Unidade WaQ Unidade: (N/m2) Momento de Inércia J = π.(d 4 – d 4)/ 32
2
1
Unidade (m4) Veloc. angular ω = 2.π.f
Unidade hz 4 CURSO ENGENHARIA DE PRODUÇÃO 2 A bomba opera com um motor que tem potência de 85 kW. Supondo que o impulsor em B esteja girando a 150 rev/min, determinar a tensão de cisalhamento máxima de torção desenvolvida em A, localizada no eixo de transmissão maçico que tem 20 mm de diâmetro. Potência P = T . ω
Unidade WaQ tensão de cisalhamento τ = M t. ρ / J Unidade: (N/m2) Veloc. angular ω = 2.π.f
Resp
τ = 3,4 GPa Unidade hz 5 •  1 Hp = 745,7 WaQs CURSO ENGENHARIA DE PRODUÇÃO 3 Um tubo de aço com diâmetro externo de 2,5 pol transmite 35 hp quando gira a 2700 rev/
min. Determinar o diâmetro interno do tubo, se a tensão de cisalhamento admissível é τmax = 67 MPa. tensão de cisalhamento t. ρ / J τ = M
Unidade: (N/m2) Potência P = T . ω
Unidade WaQ Momento de Inércia J = π.(d 4 – d 4)/ 32
Veloc. angular ω = 2.π.f
Unidade (m4) Unidade hz 2
1
6 4 aa 50 mm 3 m Fórmulas = f = 21 Hz = Ângulo de torção θ = Mt . l / G . J
Unidade (rad) Momento de Inércia J = π.d 4 / 32
Potência . ω
P=T
Veloc. angular ω = 2.π.f
Unidade WaQ Unidade (m4) Exercício 05 CURSO ENGENHARIA DE PRODUÇÃO A Resp. 64,6 MPa 1500 m B 8 Exercício 06 CURSO ENGENHARIA DE PRODUÇÃO 9 Exercício 07 CURSO ENGENHARIA DE PRODUÇÃO 10 Exercício 08 CURSO ENGENHARIA DE PRODUÇÃO 11 Exercício 09 CURSO ENGENHARIA DE PRODUÇÃO Exercício 10 12