Função seno

FUNÇÕES TRIGONOMÉTRICAS
Função seno
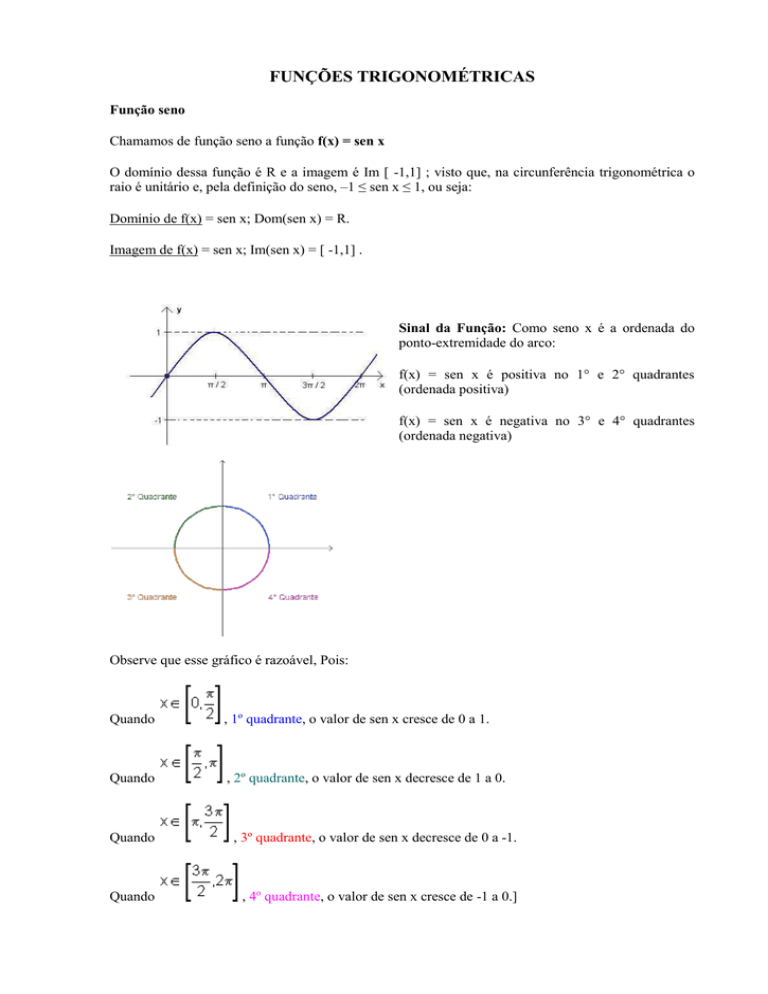
Chamamos de função seno a função f(x) = sen x
O domínio dessa função é R e a imagem é Im [ -1,1] ; visto que, na circunferência trigonométrica o
raio é unitário e, pela definição do seno, –1 ≤ sen x ≤ 1, ou seja:
Domínio de f(x) = sen x; Dom(sen x) = R.
Imagem de f(x) = sen x; Im(sen x) = [ -1,1] .
Sinal da Função: Como seno x é a ordenada do
ponto-extremidade do arco:
f(x) = sen x é positiva no 1° e 2° quadrantes
(ordenada positiva)
f(x) = sen x é negativa no 3° e 4° quadrantes
(ordenada negativa)
Observe que esse gráfico é razoável, Pois:
Quando
, 1º quadrante, o valor de sen x cresce de 0 a 1.
Quando
, 2º quadrante, o valor de sen x decresce de 1 a 0.
Quando
, 3º quadrante, o valor de sen x decresce de 0 a -1.
Quando
, 4º quadrante, o valor de sen x cresce de -1 a 0.]
Função cosseno
Chamamos de função cosseno a função f(x) = cos x.
O domínio dessa função é R e a imagem é Im [ -1,1] ; visto que, na circunferência trigonométrica o
raio é unitário e, pela definição do cosseno, –1 ≤ cos x ≤ 1, ou seja:
Domínio de f(x) = cos x; D(cos x) = R.
Imagem de f(x) = cos x; Im(cos x) = [ -1,1] .
Sinal da Função: Como cosseno x é a abscissa do ponto-extremidade do arco:
f(x) = cos x é positiva no 1° e 2° quadrantes (abscissa positiva)
f(x) = cos x é negativa no 3° e 4° quadrantes (abscissa negativa)
Observe que esse gráfico é razoável, Pois:
Quando
, 1º quadrante, o valor do cos x decresce de 1 a 0.
Quando
, 2º quadrante, o valor do cos x decresce de 0 a -1.
Quando
, 3º quadrante, o valor do cos x cresce de -1 a 0.
Quando ,
4º quadrante, o valor do cos x cresce de 0 a 1.
Função tangente
Chamamos de função tangente a função f(x) = tg x.
Domínio de f(x) = O domínio dessa função são todos os números reais, exceto os que zeram o cosseno
pois não existe cosx = 0
Imagem de f(x) = tg x; Im(tg x) = R ou
.
Sinal da Função: Como tangente x é a ordenada do ponto T interseção da reta que passa pelo centro
de uma circunferência trigonométrica e o ponto-extremidade do arco, com o eixo das tangentes então:
f(x) = tg x é positiva no 1° e 3° quadrantes (produto da ordenada pela abscissa positiva)
f(x) = tg x é negativa no 2° e 4° quadrantes (produto da ordenada pela abscissa negativa)
Função secante
Denomina-se função secante a função f(x) = 1/cos x.
Sinal da função: Como a função secante é a inversa da função cosseno, então os sinais da função
secante são os mesmos da função cosseno.
Definição:
.
Logo, o domínio da função secante é
.
Função cossecante
Denomina-se função cossecante a função f(x) = 1/sen x.
Sinal da função: Como a função cossecante é a inversa da função seno, então os sinais da função
cossecante são os mesmos da função seno.
Definição:
.
Logo, o domínio da função cossecante é
Função cotangente
Denomina-se função cotangente a função f(x) = 1/tg x ou f(x) = cos x/ sen x
Sinal da função: Como a função cotangente é a inversa da função tangente, então os sinais da função
cotangente são os mesmos da função tangente.
Definição:
Domínio:
Como a função seno se anula para arcos da forma
+k
, onde k em Z, temos:
Dom(cot)={x em R: x é diferente de (k+1)
}
Identidades trigonométricas
Fórmulas da adição
Fórmulas da multiplicação
EXERCÍCIOS:
1) Uma gráfica que confeccionou material de campanha determina o custo unitário de um de seus
produtos, em reais, de acordo com a lei C(t) = 200 + 120 . sen (  . t)/2, com t medido em horas de
trabalho. Assim, os custos máximos e mínimo desse produto são
a) 320 e 200
b) 200 e 120
c) 200 e 80
d) 320 e 80
e) 120 e 80
 sen80º   sen20º   sen130º 


 , encontraremos:
 cos10º   cos 70º   cos 40º 
2) Calculando o valor da expressão E  
a) -1
b) 1
c) sen 10°
d) cos 20°
e) sen 30°
3) Sabendo que x é do 4º quadrante e que cos x = 1/3 , calcule o valor da expressão y 
4) O menor valor de y 
a) 1/6
b) 1/5
1  senx
.
1  cos x
1
com x real é
3  cos x
c) 1/4
d) 1/2
5) Dois ângulos distintos, menores que 360°, têm, para seno, o mesmo valor positivo. A soma desses
ângulos é igual a:
a) 45°.
b) 90°.
c) 180°.
d) 270°.
e) 360°.
6) Um supermercado, que fica aberto 24 horas por dia, faz a contagem do número de clientes na loja a
cada 3 horas. Com base nos dados observados, estima-se que o número de clientes possa ser calculado
 x
 12
pela função trigonométrica f  x   900  800sen 

 , onde f(x) é o número de clientes e x, a hora

da observação (x é um inteiro tal que 0  x  24 ).
Utilizando essa função, a estimativa da diferença entre o número máximo e o número mínimo de
clientes dentro do supermercado, em um dia completo, é igual a
a) 600.
b) 800.
c) 900.
d) 1 500.
e) 1 600.
7) Observe o gráfico da função trigonométrica y = 1 + 2 sen x, a seguir.
Pode-se afirmar que o seu conjunto imagem é o intervalo
a) [-2, 1]
b) [-2, 2]
c) [-1, 2]
d) [-1, 3]
e) [-1, 4]
8) Do solo, você observa um amigo numa roda gigante. A altura h em metros de seu amigo em relação
  

   t  26   , onde o tempo t é dado em
 12 

ao solo é dada pela expressão h  t   11,5  10.sen 
segundos e a medida angular em radianos.
a) Determine a altura em que seu amigo estava quando a roda começou a girar (t = 0).
b) Determine as alturas mínima e máxima que seu amigo alcança e o tempo gasto em uma volta
completa (período).
9) O valor de (cos60° + tg45°)/sen90° é:
a) 3/2
b) 2
c)
2
d) ( 2 +1)/2
e) 0
10) O PIB (Produto Interno Bruto, que representa a soma das riquezas e dos serviços produzidos por
uma nação) de certo país, no ano 2000 + x, é dado, em bilhões de dólares, por
P(x) = 500 + 0,5x + 20cos(
x
), onde x é um inteiro não negativo.
6
Em períodos de 12 anos, o PIB do país aumenta do mesmo valor, ou seja, P(x + 12) - P(x) é constante.
Determine esta constante (em bilhões de dólares).
FUNÇÃO INVERSA
Em matemática, a função inversa de uma função
tal que
e
é, quando existe, a função
(id=função identidade). Ou seja, o que era
domínio na função original (o conjunto X neste caso, ilustrado na figura abaixo) vira imagem na
função inversa, e o que era imagem na função original (Y, neste caso - ilustrado na figura abaixo) vira
domínio.
Uma função que tenha inversa diz-se invertível. Se uma função for invertível, então tem uma única
inversa. Uma condição necessária e suficiente para que uma função seja invertível é que seja bijetora.
Somente as funções bijetoras apresentam inversa, pois qualquer número do domínio tem um único
correspondente no contradomínio (injetora) e este tem todos os seus valores relacionados uma única
vez (sobrejetora). Assim, podemos estabelecer uma relação inversa, transformando o contradomínio
em domínio, e o domínio em contra-domínio de uma função. A expressão que representa essa troca é
chamada de função inversa, e é representada por f -1(x). Ex:
Se
Portanto,
Representação Gráfica
Observa-se, pelo gráfico, que al função inversa g de uma função real de variável real f obtém-se de f
por uma simetria em relação à recta y = x
FUNÇÕES TRIGONOMÉTRICAS INVERSAS
Em matemática, as funções trigonométricas inversas são as inversas das funções trigonométricas.
Algumas vezes são chamadas de função de arco, pois retornam o arco correspondente a certa função
trigonométrica.
Pela definição de função inversa, uma função f, de domínio D possui inversa somente se f for bijetora,
por este motivo nem todas as funções trigonométricas possuem inversas em seus domínios de
definição, mas podemos tomar subconjuntos desses domínios para gerar novas função que possuam
inversas.
Exemplo: A função f(x)=cos(x) não é bijetora em seu domínio de definição que é o conjunto dos
números reais, pois para um valor de y correspondem infinitos valores de x. Por exemplo, se cos(x)=1,
podemos tomar x=0, x=2
, x=4
, x=-2
, etc, isto é x=2k
, onde k é um número inteiro, isto quer
dizer que não podemos definir a inversa de f(x)=cos(x) em seu domínio. Devemos então restringir o
domínio para um subconjunto dos números reais onde a função é bijetora.
Como as funções trigonométricas são periódicas, existem muitos intervalos onde elas são bijetoras. É
usual escolher como domínio, intervalos onde o zero é o ponto médio ou o extremo esquerdo e no qual
a função percorra todo seu conjunto imagem.
Função Arco Seno
Consideremos a função f(x)=sen(x), com domínio no intervalo [-
/2,
/2] e imagem no intervalo [-
1,1]. A função inversa de f, denominada arco cujo seno, definida por f-1:[-1,1]
[-
/2,
/2] é
denotada por
f-1(x) = arcsen(x)
Gráfico de Arco-seno
Função Arco-cosseno
Seja a função g(x)=cos(x), com domínio [0, ] e imagem [-1,1]. A função inversa de f, denominada
arco cujo cosseno é definida por g-1:[-1,1] [0, ] e denotada por
g-1(x) = arccos(x)
Gráfico de Arco-cosseno
Função Arco-tangente
Dada a função f(x)=tg(x), com domínio (denominada arco-tangente é definida por f-1:R
/2, /2) e imagem em R, a função inversa de f,
(- /2, /2) e denotada por
f-1(x) = arctg(x)
Gráfico de Arco-tangente
Função Arco-cotangente
Dada a função f(x)=cotg(x), com domínio (0, ) e imagem em R, a função inversa de f, denominada
arco-cotangente é definida por f-1:R (0, ) e denotada por
f-1(x) = arccotg(x)
Gráfico de Arco-cotangente
Resumo: Funções trigonométricas inversas