Notas de aula 07

Universidade Tecnológica Federal do Paraná
Professor Murilo V. G. da Silva
Notas de aula – Algoritmos Avançados I (Aula 07)
Conteúdos da Aula: [DPV06 cap. 7]
1. Programação Linear 101
Entrada:
ˆ Conjunto de equações/desigualdades lineares com variáveis x1 , ..., xn ;
ˆ Uma função objetivo f a ser maximizada/minimizada.
Saı́da:
ˆ Valores para x1 , ..., xn que maximizam/minimizam f respeitando as equações/desigualdades.
Exemplo: Maximização de lucros em uma chocolateria que produz os seguintes produtos:
(1) Chocolate Pyramide
(2) Chocolate Pyramide Nuit
Considere as seguintes condições:
ˆ Lucro com venda de uma caixa de (1): $1,00.
ˆ Lucro com venda de uma caixa de (2): $6,00.
ˆ Demanda diária por (1): 200 caixas.
ˆ Demanda diária por (2): 300 caixas.
ˆ Capacidade de produção da fábrica: 400 caixas diárias.
Pergunta: Quanto devemos produzir de (1) e (2) diariamente para maximizar o lucro?
ˆ Vamos chamar de x1 a quantidade de caixas de (1)
ˆ Vamos chamar de x2 a quantidade de caixas de (2)
Com isso queremos maximizar a função objetivo x1 + 6x2 e as restrições são:
x1 ≤ 200
x2 ≤ 300
x1 + x2 ≤ 400
x1 , x2 ≥ 0
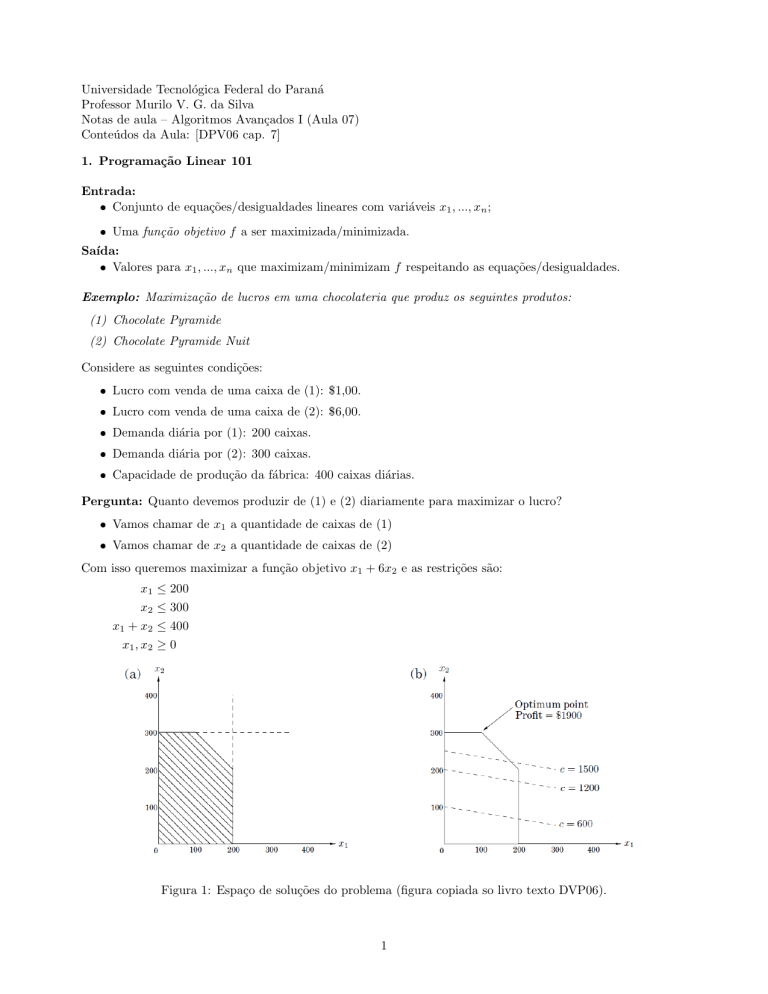
Figura 1: Espaço de soluções do problema (figura copiada so livro texto DVP06).
1
Olhando o gráfico da Figura 1 (a) temos um polı́gono em que cada aresta vem de uma equação do conjunto
de restrições. Qualquer valor que satisfaça as restrições (sem necessariamente maximizar a função objetivo) deve
pertencer ao polı́gono. Qualquer um destes valores são chamados de soluções factı́veis. Na Figura 1 (b) cada
linha pontilhada representa uma reta da função x1 + 6x2 = c para diferentes valores de lucro c. Claramente, o
valor máximo que c pode atingir é quando a função objetivo passa no ponto (100, 300). Tal ponto é chamado
de solução ótima.
Neste curso veremos apenas os conceitos básicos de como se modelar problemas usando programação linear
e não apresentaremos os algoritmos que resolvem de fato os problemas. Convidamos os alunos, entretanto, a
pesquisar sobre os diferentes algoritmos utilizados nesta área. A ideia básica que queremos que o aluno entenda
neste momento (embora não demonstraremos aqui) é que a solução do problema de programação linear sempre
se encontra em um dos vértices do polı́gono (ou poliedro n-dimensinal, onde n é o número de variáveis) convexo
obtido a partir das restrições do problema.
Novo Exemplo: Digamos que temos um terceiro tipo de chocolate cujo lucro é de $13,00 por caixa. Digamos
que neste novo cenário aparecem outras restrições modeladas pelas equações extras que aparecem abaixo:
Maximizar x1 + 6x2 + 13x3 dadas as restrições:
x1 ≤ 200
x2 ≤ 300
x1 + x2 ≤ 400
x2 + x3 ≤ 600
x1 , x2 , x3 ≥ 0
Figura 2: Novo espaço de soluções do problema, agora com 3 variáveis (figura copiada so livro texto DVP06).
Neste caso a solução ótima é (0, 300, 100) com valor 3100 para a função objetivo. No gráfico da figura 2,
é mostrado a sequência de passos que o Algoritmo Simplex usa para chegar na solução. O algoritmo percorre
cada um dos vértices do poliedro sempre movendo-se para um vértice adjacente que tenha um maior valor para
a função objetivo.
2
Novo Exemplo: Planejamento de Produção em uma fábrica
Digamos que temos em mãos os dados da demanda experada pelos produtos fabricados em cada mês.
Chamaremos estes números de d1 , d2 , ..., d12 e que temos inicialmente w0 = 30 funcionários e não temos nenhum
produto estocado, que denotaremos por s0 = 0. Além disso sabemos o seguinte:
ˆ Produtividade dos trabalhadores: 80 produtos (mês)
ˆ Salário dos trabalhadores: $2000.00 (mês)
ˆ Hora Extra: Um produto produzido em hora extra custa 80% mais
ˆ Hora Extra: Um trabalhador em hora extra produz 30% a mais
ˆ Custo para contratar: $320.00
ˆ Custo para demitir: $400.00
ˆ Custo de armazenamento de produtos: $8.00 (mês)
Queremos determinar o valor de diversas variáveis:
ˆ Produtos a serem fabricados em cada mês: x1 , x2 , ..., x12
ˆ Produtos a serem armazenados em cada mês: s1 , s2 , ..., s12
ˆ Quantidade de funcionários em cada mês: w1 , w2 , ..., w12
ˆ Produtos fabricados durante hora-extra: o1 , o2 , ..., o12
ˆ Quantidade de funcionários contratados: h1 , h2 , ..., h12
ˆ Quantidade de funcionários demitidos: f1 , f2 , ..., f12
Vamos as equações:
Minimizar: 2000
12
P
wi + 320
i=1
12
P
i=1
hi + 400
12
P
fi + 8
i=1
12
P
si + 180
i=1
12
P
oi
i=1
Restrições:
xi = 20wi + oi
wi = wi−1 + hi − fi
si = si−1 + xi − di
oi ≤ 6wi
Além disso, obviamente temos xi , si , wi , oi , hi , fi ≥ 0
Problema: O que significa demitir 3.25 funcionários? Pense a respeito.
3
Versão “padrão” de um problema de PL
Primeiro observe que dado um problema de maximização de uma função objetivo, é fácil obter um problema equivalente de minimização (e vice-versa) apenas multiplicando cada coeficiente da função objetivo por
-1. Além disso veremos que equações podem ser transformadas em inequações e vice-versa. Finalmente veremos
se tivermos variáveis com domı́nio igual a R, podemos mudar o problema para que tenhamos domı́nio apenas
com valores maiores ou iguais a 0.
Maximização para minimização:
max x1 − 6x2 torna-se min −x1 + 6x2 .
Uma equação vira duas inequações:
ax = b é equivalente as duas inequações ax ≤ b, ax ≥ b .
Uma inequação vira uma equação (+ uma variável “dummy”):
n
P
ai xi ≤ b, podemos adicionar uma variável “dummy” s com domı́nio não negativo e obter:
Dada a equação
i=1
n
X
ai xi + s = b
i=1
s≥0
Domı́nio das variáveis R para domı́nio apenas com valores positivos:
Basta trocar cada variável x com domı́nio R por duas variáveis x0 , x00 ≥ 0 e onde aparecia x nas equações
agora aparece x0 − x00
Moral da história: Com isso podemos assumir que nossos problemas de PL sempre são de minimização, com
equações (igualdades) e com variáveis assumindo valores ≥ 0.
Fluxo em Redes
Dada uma rede com capacidade nas arestas, nosso objetivo agora é enviar a maior quantidade de “produtos”
de uma origem para um destino respeitando as capacidades das arestas da rede. Por exemplo, se a rede é uma
malha de oleodutos, a capacidade de uma aresta é a quantidade máxima de petróleo que um determinado duto
admite por unidade de tempo. Se por exemplo estivermos tratando de uma rede de transporte rodoviário, a
capacidade de uma aresta é a quantidade máxima de veı́culos que podem trafegar em uma determinada via por
unidade de tempo.
O problema é modelado com um grafo G = (V, E) (normalmente direcionado) com capacidades positivas
nas arestas c : E → R+ e dois véritices especiais s, t ∈ V de origem e destino respectivamente.
Figura 3: (a) Grafo com capacidades nas arestas. (b) Um fluxo máximo (figuras do livro texto DVP06).
4
A ideia é determinar a quantidade máxima de produtos que podem ser enviados de s a t de maneira que
dada uma aresta uv ∈ E não se pode enviar mais produtos pela aresta uv do a capacidade c(uv). Além disso o
fluxo tem que ser “coerente”, ou seja, a quantidade de produtos chegando em um vértice u tem que ser igual
a quantidade de objetos saindo de u (exceto o vértice s do qual temos apenas produtos saindo e o vértice t no
qual temos apenas produtos chegando.
Para resolver o problema a ideia é calcular uma função de fluxo f : E → R+ que associa um fluxo de
produtos para cada aresta de G. Este fluxo tem que respeitar o seguinte:
(1) ∀uv ∈ E, 0 ≤ f (uv) ≤ c(uv)
P
(2) ∀x ∈ V \ {s, t},
f (vx) =
v;vx∈E
P
f (xv)
v;xv∈E
O fluxo obtido é soma dos fluxos das arestas saindo de s, ou seja,
P
se o mesmo valor de
f (vt)).
P
f (sv) (observe que este valor deve
v;sv∈E
v;vt∈E
Como encontrar um fluxo máximo:
(ideia do algoritmo visto em sala)
Certificado de Otimalidade: Corte Mı́nimo:
(visto em sala)
Modelando fluxo máximo como programação linear:
(visto em sala)
Dualidade em programação linear:
Assim como temos um problema de minimização associado ao problema de fluxo máximo (no caso o problema de corte mı́nimo), temos um problema de minimização associado a qualquer problema de maximização
em programação linear (assim como sempre há um problema de maximização associado a cada problema de minimização). Vamos mostrar isso voltando ao nosso problema da fábrica de chocolates, onde tı́nhamos formulado
o problema da seguinte maneira:
max x1 + 6x2
x1 ≤ 200
x2 ≤ 300
x1 + x2 ≤ 400
x1 , x2 ≥ 0
Pergunta: O solução que obtivemos foi (100, 300). Como podemos nos certificar de que a solução ótima?
(Ou seja, que o valor máximo que x1 + 6x2 pode atingir é 1900?)
Se somarmos a primeira restrição com a segunda multiplicada por seis obtemos a seguinte equação que é um
limitante superior para a função objetivo:
ˆ x1 + 6x2 ≤ 2000
Chegamos quase lá, mas isso não é bom o suficiente. Com um pouco de perspicácia podemos ver que
multiplicando a primeira, a segunda e a terceira restrição respectivamente por 0, 5 e 1 e somarmos as três
equações chegamos em
ˆ x1 + 6x2 ≤ 1900
Ou seja, a função objetivo não pode atingir um valor maior do que 1900. Como nossa solução (100, 300)
atinge este valor, a solução é ótima. Em particular, o vetor (0, 5, 1) é um certificado de otimalidade.
5
O que acontece se buscarmos sistematicamente o vetor (0,5,1)?
Veremos agora o que acontece se o invés de advinhar o vetor (0, 5, 1), tentarmos sistamticamente obter tal
vetor. Vamos chamá-lo de (y1 , y2 , y3 ).
ˆ Fato 1: y1 , y2 , y3 ≥ 0 (caso contrário o sentido da desigualdade mudaria)
ˆ Fato 2: Multiplicando a i-ésima restrição por yi e somando as três equações obtemos:
(y1 + y3 )x1 + (y2 + y3 )x3 ≤ 200y1 + 300y2 + 400y3
Como queremos que o lado esquerdo tenha a forma da nossa função objetivo em que os coeficientes são 1
e 6, basta restringir que (a) y1 + y3 = 1 e (b) y2 + y3 = 6. No caso de obtivermos o nosso certificado dizendo
que uma função objetivo c1 x1 + c2 x2 ≤ 1900 para valores c1 ≥ 1 e c2 ≥ 6 isso também serve dado o sentido da
desigualdade. Ou seja, as restrições (a) e (b) podem ser vistas como
ˆ Fato 3: y1 + y3 ≥ 1 e y2 + y3 ≥ 6.
Como estamos em busca de um limitante superior mais “apertado” possı́vel, queremos minimizar o lado
direito da desigualdade do Fato 2. Juntando tudo temos:
min 200y1 + 300y2 + 400y3
y1 + y3 ≥ 1
y2 + y3 ≥ 6
y1 , y2 , y3 ≥ 0
Ou seja, outro problema de PL!
Esse novo problema de PL é chamado de dual do problema original, que é chamado de problema primal.
Veja que qualquer solução factı́vel para o problema dual oferece um limitante superior para o valor ótimo do
problema original. Se acharmos uma solução factı́vel cujo valor objetivo seja igual no primal e no dual, esta
solução deve ser ótima. Este é o caso das soluções x1 = 100, x2 = 300 e y1 = 0, y2 = 5, y3 = 1. Para estes
valores, a função objetivo de ambos problemas (um de minimização e outro de maximização) tem valor 1900.
Não é difı́cil generalizar todo este raciocı́nio e ver que todo problema de PL de maximização tem um dual
de minimização e vice-versa de acordo com a Figura 4 abaixo:
Figura 4: Um problema de maximização e seu dual de minimização.
6