matriz fundamental

Visão Computacional
CPS754
aula 12 - matriz fundamental
Antonio Oliveira
Ricardo Marroquim
1/1
visão computacional
tópicos
métodos numéricos para computar F
2/1
básico
equação básica
lembrando da condição
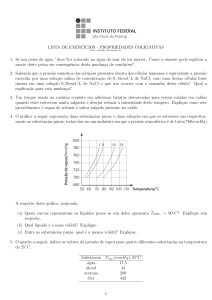
x0 Fx = 0
X
epipolar plane
x
C
π
x/
C
/
3/1
básico
equação básica
lembrando da condição
T
x0 Fx = 0
assim como resolvemos a DLT para homografia planar,
podemos usar correspondências para resolver este problema
com pares suficientes xi ↔ x0i a matriz F pode ser computada
  0

x
f11 f12 f13
x y 1 f21 f22 f23  y 0  = 0
1
f31 f32 f33
x0 xf11 + x0 yf12 x0 f13 + y 0 xf21 + y 0 yf23 + xf31 + yf32 + f33 = 0
4/1
básico
equação básica
separando os termos de f e tornando em um produto escalar
(x0 x, x0 y, x0 , y 0 x, y 0 y, y 0 , x, y, 1)f = 0
com as correspondências montamos o sistema
 0
x1 x1 x01 y1 x01 y10 x1 y10 y1 y10 x1
 ..
..
..
..
..
..
..
 .
.
.
.
.
.
.
x0n xn x0n yn x0n yn0 xn yn0 yn yn0 xn
Af = 0

y1 1
.. ..  f = 0
. .
yn 1
podemos achar F como nos outros métodos usando a SVD
o vetor singular correspondente ao menor valor singular de A
ou seja, última coluna de V onde SVD A = UDVT
qual o problema deste método?
5/1
singularidade
restrição de F
F tem posto 2
se não forçamos esta restrição, linhas epipolares l0 = Fx
variando x não coincidirão no mesmo ponto epipolar
6/1
singularidade
restrição de F
a matriz F em geral não terá posto 2 computada usando o
método de correspondências (equações lineares)
é preciso forçar esta restrição
existe um método muito simples:
se SVD F = UDVT onde D = diag(r, s, t)
substituir por F̃ = Udiag(r, s, 0)VT
7/1
singularidade
aproximação posto baixo
esta aproximação está baseada na norma de Frobenius
v
v
umin{m,n}
uX
m X
n
u X
u
kAkF = t
σi2
|aij |2 = t
i=1 j=1
i=1
onde σ são os valores singulares de A
onde queremos minimizar kA − ÃkF sujeito a rank(Ã) = r e
detà = 0
intuitivamente, devemos diminuir a diferença entre os valores
singulares, com a restrição de que alguns valores singulares de
à são zero
8/1
singularidade
aproximação matriz ortogonal
este mesmo método pode ser utilizado para encontrar a
matriz ortogonal R mais próxima de A
como o SVD de uma matriz ortogonal é UIVT , substituimos
A = UDVT por Aortogonal = UVT
aplicado também no problema de Procrustes Ortogonal:
encontrar a matriz ortogonal que melhor leva B em C
R = argminΩ kBΩ − CkF , onde ΩT Ω = I
neste caso é equivalente a encontrar a matriz ortogonal mais
próxima de A = BT C
9/1
singularidade
aproximação matriz ortogonal
o problema de Procrustes Ortogonal pode ser estendido para
encontrar apenas matrizes de rotação (i.e. determinante = 1)
aplicação importante na área de visão computacional
neste caso modificamos a matriz diagonal de A = UDVT por
R = UD0 VT
onde D0 é a matriz D modificada:
substituir o menor valor singular de D por det(UVT ) e o
restante da diagonal pelo valor 1
garante que o determinante de R é positivo
10 / 1
singularidade
algoritmo
dados 8 ou mais correspondências
1
2
3
4
normalizar as coordenadas: x̂i = Txi e x̂0i = T0 x0i
computar a matriz F̂ usando o método linear
ˆ
colocar a restrição e computar F̃
0 ˆ
desnormalizar: F = T T F̃T
11 / 1
caso mı́nimo
7 correspondências
com posto 8 é possı́vel resolver a matriz F a menos de uma
escala
quando temos apenas 7 correspondências temos uma matriz
7 × 9 com posto 7 (geralmente)
ainda é possı́vel resolver utilizando a restrição de singularidade
a solução de Af = 0 tem a forma
αF1 + (1 − α)F2
matrizes F1 e F2
geradores f1 e f2 do espaço nulo a direita de A
12 / 1
caso mı́nimo
7 correspondências
com a restrição de que detF = 0
det(αF1 + (1 − α)F2 ) = 0
como sabemos F1 e F2
chegamos a um polinômio cúbico em α
existem 1 ou 3 soluções reais para este problema
quando usar então a solução mı́nima?
13 / 1
algoritmo automático
computando F automaticamente
problema: a partir de 2 imagens estimar automaticamente F
utilizar RANSAC de uma maneira similar ao último trabalho
(panorâmica)
utilizar algoritmo do caso mı́nimo (7 correspondências)
não é necessário forçar o posto 2
o número de amostragens para o RANSAC é menor
s
| 5%
7
8
|
|
4
5
10%
20%
25%
30%
40%
50%
8
9
20
26
33
44
54
78
163
272
588
1177
no caso de 3 soluções possı́veis todas são testadas e é mantida
aquela com maior número de inliers
14 / 1
algoritmo automático
medida de erro
minimizando o erro geométrico após o RANSAC
X
d(xi , x̂i )2 + d(x0i , x̂0i )2
i
xi ↔ x0i são correspondências medidas
x̂i e x̂0i são correspondências corretas que satisfazem
0
exatamente x̂iT Fx̂i = 0
15 / 1
algoritmo automático
medida de erro
minimizando o erro geométrico com algoritmo não-linear
definir um par de câmeras P = [I|0] e P0 = [M|t]
definir pontos 3D Xi que projetam em
x̂i = PXi e x̂0i = P0 Xi
o algoritmo varia Xi e P0 para minimizar o erro
X
d(xi , x̂i )2 + d(x0i , x̂0i )2
i
finalmente teremos F = [t]× M
veremos mais adiante como estimar os pontos 3D Xi para
cada correspondência xi ↔ x0i
16 / 1
algoritmo automático
medida de erro
pode-se usar por exemplo Levenberg-Marquardt para iterar o
algoritmo
ao final de cada iteração estipula-se a nova matriz F
pode-se então encontrar novas correspondências procurando
ao longo das linhas epipolares
limita-se a busca aos pixels ao longo de uma faixa da linha
epipolar
com os novos pontos realiza-se uma nova iteração
17 / 1
resultado
imagens originais 640x480 pixels
18 / 1
resultado
corners detectados
19 / 1
resultado
todas correspondências e somente outliers
20 / 1
resultado
inliers e conjunto final adicionando mais correspondências
21 / 1
câmera calibrada
computando E
como no caso anterior pode-se encontrar E a partir de 8
correspondências
T
x0 i Exi = 0
além de satisfazer a condição detE = 0
existe a condição extra de que os dois valores singulares sejam
iguais
neste caso pode-se substituir D = diag(a, b, c) por
D̂ = diag((a + b)/2, (a + b)/2, 0)
onde Ê = UD̂VT é a matriz essencial mais próxima a E de
acordo com a norma de Frobenius
22 / 1
outras restrições
retas
note que retas correspondentes não adicionam nenhuma
restrição ao problema de se encontrar F
no caso de pontos:
um ponto da imagem é reprojetado definindo a reta
em geral duas retas no espaço 3D não se intersectam
porém se um par de correspondências geram retas
intersectantes, colocam uma restrição na geometria epipolar
no caso de retas
retas são reprojetadas como planos no espaço 3D
um par de retas geram dois planos, que sempre se intersectam
por isso não geram uma restrição
porém, no caso de retas paralelas, a correspondência dos
pontos de fugas gera uma restrição
23 / 1