teoria - Física Vivencial

1
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE TEORIA
1 INTRODUÇÃO Os assuntos tratados a seguir são de importância fundamental não somente na Matemática, mas também na Física, Química, Geografia, Estatística e outras disciplinas. A linguagem Matemática é importante para representar algebricamente ou graficamente o estudo, por exemplo, do movimento uniforme e outros fenômenos. 2 PAR ORDENADO Consideremos os conjuntos A = {x , y} e B = {y , x} . Lembrando que dois conjuntos que diferem apenas pela ordem de seus elementos são iguais, então, A = B. Em alguns casos, a ordem dos elementos é importante, então não podemos colocá‐los como elementos de um conjunto, e sim como elementos de pares ordenados, ou seja, (x , y) e (y , x). Assim sendo: (x , y) ≠ (y , x). Dois pares ordenados (a , b) e (c , d) são iguais se, e somente se, a = c e b = d. Por exemplo: numa escola, ficou estabelecido que, no final de cada bimestre do ano letivo seria publicada uma tabela com pares ordenados de números onde o primeiro seria o número de chamada do aluno, e o segundo, a nota correspondente. Desta maneira, o par (5 , 8) quer dizer que o aluno de número 5 obteve nota 8 e o par (8 , 5) quer dizer que o aluno de número 8 obteve nota 5. 3 PRODUTO CARTESIANO Dados dois conjuntos A e B, chama‐se produto cartesiano de A por B e será indicado por A x B, que se lê A cartesiano B ao conjunto formado por todos os pares ordenados possíveis, tendo o primeiro elemento pertencente ao conjunto A e o segundo elemento pertencente ao conjunto B. Exemplificando: consideremos os conjuntos A = {1 , 2 , 5} e B = {3 , 6} e vamos formar os produtos A x B e B x A. A x B = { (1 , 3) , (1 , 6) , (2 , 3) , (2 , 6) , (5 , 3) , (5 , 6) } B x A = { (3 , 1) , (3 , 2) , (3 , 5) , (6 , 1) , (6 , 2) , (6 , 5) } Observe que: 1º) A x B ≠ B x A 2º) Se n (A x B) é o número de elementos de A x B , n (A) é o número de elementos do conjunto A, 2
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE n (B) é o número de elementos do conjunto B, então, n (A x B) = n (A) x n (B). 4 SISTEMA CARTESIANO DE EIXOS ORTOGONAIS Os elementos de um conjunto numérico podem ser representados por pontos de uma reta orientada. Os pares ordenados (x , y) de números reais são representados por pontos do plano. Consideremos no plano duas retas perpendiculares, orientadas, que dividem o plano em quatro regiões denominadas de quadrantes, que são numerados da seguinte forma: SISTEMA CARTESIANO DE EIXOS ORTOGONAIS Figura 1 O ponto de interseção dos eixos é o ponto O, denominado origem do sistema cartesiano de eixos ortogonais. Consideremos o ponto P(x, y). O primeiro elemento x recebe o nome de abscissa e o segundo elemento recebe o nome de ordenada. As abscissas são positivas à direita do eixo das ordenadas e negativas à esquerda. As ordenadas são positivas acima do eixo das abscissas e negativas abaixo. Exemplificando: Vamos determinar as coordenadas dos pontos dados no sistema abaixo. 3
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE 5
B A 4
3
2
D 1
G E ‐5 ‐4 ‐3 ‐2 ‐1 0 1 2 3 4 5 -1
C -2
-3
F -4
A (2,4) , B (‐1,5) , C (‐2,‐1) , D (‐3 , 1) , E (5,0) , F (0,‐4) e G (‐5,0) COORDENADA DOS PONTOS Figura 2 5 CONSTRUINDO GRÁFICOS A PARTIR DE DADOS EXPERIMENTAIS Tanto na pesquisa quanto no ensino é comum surgir a necessidade de se construir um gráfico, a partir de dados obtidos experimentalmente. A seguir, alguns exemplos serão mostrados para ilustrar o procedimento de construção de um gráfico, a partir de dados experimentais. 5.1 GRÁFICO DA POSIÇÃO EM FUNÇÃO DO TEMPO REFERENTE AO MOVIMENTO DE UMA PARTÍCULA O gráfico de uma Função Polinomial do Primeiro Grau é uma reta, portanto, y = ax + b é a equação de uma reta. O coeficiente a recebe o nome de coeficiente angular ou declive da reta que é a tangente do ângulo θ que a reta forma com o sentido positivo do eixo das abscissas. O ângulo θ é chamado de inclinação da reta. O coeficiente b é chamado coeficiente linear da reta. 4
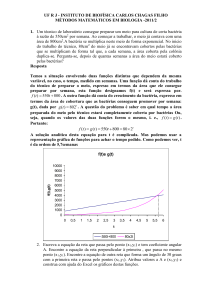
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE Na Física a equação do movimento uniforme é s = s0 + vt onde s é o espaço percorrido pelo móvel no tempo t, s0 é o espaço inicial percorrido pelo móvel e v a velocidade escalar. Vamos construir o gráfico de S = ‐ 6 +2t, com as posições S em metros e os instantes t medidos em segundos. Como o gráfico é uma reta bastam dois pontos para representá‐la no plano. Escolheremos dois valores quaisquer para t e teremos os correspondentes para S. t = 1 ⇒ S = ‐4 e para t = 4 ⇒ S = 2. Temos assim os ponto P (1 , ‐4) e Q (4, 2). S(m) t(s)
Figura 3 6. GRÁFICO CARTESIANO DA FUNÇÃO POLINOMIAL O gráfico cartesiano da função polinomial do segundo grau é uma curva denominada parábola. Para construção do gráfico escolhemos alguns valores para x e obtemos os correspondentes valores de y. Exemplos. Vamos construir os gráficos das funções: 5
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE 1) y = x2 + x ‐ 2 Tabela 1 x y ‐2 0 ‐1 ‐2 0 ‐2 1 0 2 4 Figura 4 2) y = ‐ x2 + 2x + 3 Tabela 2 x y ‐2 ‐5 ‐1 0 0 3 1 4 2 3 Figura 5 Os dois gráficos mostram que: 1) se a > 0 a concavidade da parábola é voltada para cima. 2) se a < 0 a concavidade da parábola é voltada para baixo. No primeiro caso existe um ponto V da parábola que tem a menor ordenada e é chamado de ponto de mínimo da função. No segundo caso o ponto V é o ponto que tem a maior ordenada e é chamado de ponto de máximo da função. O ponto V de mínimo ou máximo da função é o vértice da parábola e tem como abscissa x =−
Δ⎞
b
Δ
⎛ b
,− ⎟ . e como ordenada y = −
, isto é, V = ⎜ −
2a
4a
⎝ 2a 4a ⎠
6
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE ⎛ 1 9⎞
,− ⎟ e da segunda é V (1, 4). ⎝ 2 4⎠
Voltando aos exemplos anteriores, o vértice da primeira parábola é V ⎜ −
A reta que passa por V e é paralela ao eixo das ordenadas recebe o nome de eixo de simetria da parábola. Para cada ponto P da parábola existe um ponto P’ da mesma , tal que P e P’ estão numa mesma perpendicular a este eixo e à mesma distância do mesmo. Podemos agora estabelecer o conjunto imagem Im da função f( x ) = ax2 + bx +c, onde a ≠ 0 , que tem como domínio D = R e como contradomínio C = R, já que sabemos como obter os pontos de máximo ou mínimo da mesma. Se a > 0 a função tem um mínimo dado por y = −
Δ⎫
Δ
⎧
, portanto, Im = ⎨ y ∈ R y ≥ −
⎬ 4a ⎭
4a
⎩
Se a < 0 a função tem um máximo dado por y = −
Δ⎫
Δ
⎧
, portanto, Im = ⎨ y ∈ R y ≤ −
⎬ 4a ⎭
4a
⎩
Já vimos que o procedimento para se fazer o gráfico de uma função polinomial do segundo grau é: 1)Escolher alguns valores para x e através do critério da função obter os correspondentes valores de y. 2) Marcar no sistema cartesiano os pontos de coordenadas ( x, y ). 3) Unir os pontos. Uma outra maneira para se construir o gráfico é: 1) Verificar, inicialmente, através do coeficiente a, a concavidade da parábola. Se a > 0 a concavidade é voltada para cima, se a < 0 a concavidade é voltada para baixo. Δ⎞
⎛ b
,− ⎟ da parábola. ⎝ 2a 4a ⎠
2) Determinar o vértice V ⎜ −
3) Determinar as raízes. Se Δ > 0 a parábola intercepta o eixo das abscissas nos pontos ( x1, 0) e (x2, 0). Se Δ = 0 a parábola tangencia o eixo das abscissas no ponto (x1, 0). Se Δ < 0 a parábola não tem ponto em comum com o eixo das abscissas. 4) Traçar o eixo de simetria da parábola. 5) Determinar o ponto ( 0, c ) de interseção da parábola com o eixo das ordenadas. 6) Se os pontos obtidos não forem suficientes porque quando Δ < 0 não temos os pontos de interseção ou tangência da parábola com o eixo das abscissas, então, determinamos mais alguns pontos como foi feito nos dois exemplos iniciais. 7) Unindo‐se os pontos assinalados temos a parábola. 6.1 SINAIS DA FUNÇÃO Vamos verificar para que valores reais de x a função y = ax2 + bx + c e a ≠ 0 é positiva ou negativa. 7
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE 1) Δ > 0 ⇒ a função tem duas raízes reais e distintas, isto é, x1 ≠ x2 A função tem o sinal de a para valores externos ao intervalo das raízes e sinal contrário ao de a para valores internos. Na reta orientada temos: Figura 6 Figura 7 Lembrar que para x = x1 ou x = x2 f(x) = 0 2) Δ = 0 ⇒ a função tem duas raízes reais e iguais, isto é, x1 = x2 A função tem o sinal de a para todo x diferente da raiz. Na reta orientada temos: Figura 8 Figura 9 Lembrar que para x = x1 ou x = x2 f(x) = 0 8
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE 3) Δ < 0 ⇒ a função não tem raízes reais A função tem o sinal de a para qualquer valor real de x. Na reta orientada temos: Figura 10 Figura 11 Exemplos. Para que valores reais de x a função f( x ) é, respectivamente, a) positiva, b) negativa, c)nula. 1) f( x ) = x2 ‐ 11x + 2 Calculando as raízes de x2 ‐ 11x + 28. Δ = ( ‐ 11 )2 ‐ 4x1x28 ⇒ Δ = 121 ‐ 112 = 9 x=
11 ± 9 11 ± 3
=
⇒ x1 = 7 e x 2 = 4 2 x1
2
Na reta orientada temos os sinais de f( x ): a) a função f( x ) é positiva para x < 4 ou x > 7. b) a função f( x ) é negativa para 4 < x < 7. c) a função f( x ) é nula para x = 4 e x = 7. 2) f( x ) = ‐ 2x2 + 5x Vamos calcular as raízes de ‐ x2 + 5x = 0 empregando a fatoração: x( ‐ 2x + 5 ) = 0 Podemos concluir que x = 0 ou ‐ 2x + 5 = 0 e x =
5
2
Poderíamos ter resolvido a equação através da fórmula de Bhaskara. Na reta orientada temos os sinais de f( x ): 9
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE a) a função f( x ) é positiva para 0 < x < 5
2
b) a função f( x ) é negativa para x < 0 ou x > c) a função f( x ) é nula para x = 0 e x = 5
2
5
2
3)f( x ) = 3x2 ‐ x + 1 Calculando as raízes de 3x2 ‐ x + 1 Δ = ( ‐ 1 )2 ‐ 4x3x1 = 1 ‐ 12 = ‐11 A função não tem raízes reais porque o discriminante é negativo Na reta orientada temos os sinais de f( x ): a) a função f( x ) é positiva para qualquer valor real de x. b) não existe x real para que a função f( x ) seja negativa. c) não existe x real para que a função f( x ) seja igual a zero. 7. INEQUAÇÕES Resolver em R as inequações: 1) x2 ‐ 5 ≤ 0 Para estudar os sinais de y = x2 ‐ 5 devemos, inicialmente, calcular as raízes. x2 ‐ 5 = 0 ⇒ x2 = 5 ou x = ± 5 . Temos, então, x1 = − 5 ou x = 5 Indicando na reta orientada os sinais de y: O exercício pede y ≤ 0 . Resposta: − 5 ≤ x ≤ 5 2) ( ‐ x2 + 2x + 8 )( 2x2 ‐ 11x + 5 ) > 0 Vamos verificar os sinais de y1 = ‐ x2 + 2x + 8 e y2 = 2x2 ‐ 11x + 5 As raízes de ‐ x2 + 2x + 8 são x1 = ‐ 2 e x2 = 4 Indicando na reta orientada os sinais de y1 : 10
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE As raízes de 2x2 ‐ 11x +8 são x1 = 1
e x2 = 5 2
Indicando na reta orientada os sinais de y2: Para estudarmos os sinais de y1y2 vamos organizar uma tabela dispondo os valores de x em ordem crescente e os sinais de y1 e y2. Tabela 3 O exercício pede y1y2 > 0. Resposta: ‐ 2 < x < 1/2 ou 4 < x < 5 (− x 2 + 4 x)(3x 2 + 2 x − 5)
≤ 0 3) 3x + 2
Condição de existência da fração: x ≠ −
2
. O denominador não pode ser igual a zero. 3
Vamos estudar os sinais de y1 = ‐ x2 + 4x, y2 = 3x2 + 2x ‐ 5 e y3 = 3x + 2. Precisamos, portanto, das raízes. As raízes de y1 são x1 = 0 e x2 = 4 Sinais de y1 : As raízes de y2 são x1 = −
5
e x2 = 1 Sinais de y2 : 3
A raiz de y3 é x = −
2
Sinal de y3 : 3
11
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE Tabela 4 O exercício pede y1 y 2
5
2
≤ 0 . Resposta: − ≤ x < − ou 0 ≤ x ≤ 1 ou x ≥ 4 3
3
y3
Para saber mais: http://www.educ.fc.ul.pt/icm/icm2000/icm28/func/quapar.htm Os exemplos apresentados procuram ilustrar a importância que os gráficos apresentam quando se está precisando correlacionar dados que foram obtidos a partir de um experimento. As informações oferecidas pelo gráfico podem ser utilizadas para se tirar conclusões ou se fazer novas perguntas a respeito de uma investigação científica, enriquecendo assim o processo de produção de conhecimento a respeito de um dado assunto. Autores: •
Abrão Arid Netto . Autoria Especializada em Física (conteúdos: Laboratório Virtual, Teoria, Mapa Interativo, Avaliação e Guia do Professor): Formação Acadêmica*Licenciado em Matemática pela Faculdade de Filosofia Ciências e Letras da Universidade Mackenzie. Cursos de aperfeiçoamento* Grupo de Estudos do Ensino da Matemática.* Centro de Treinamento para Professores de Ciências (CECISP).* Curso de Lógica Matemática na Faculdade de Filosofia Ciência e Letras "Sedes Sapientiae".* Curso Teórico Prático de Física Experimental do Museu de Ciências ‐ São Paulo.Atividades de magistério * Professor de Matemática da 12
CONSTRUINDO E ANALISANDO GRÁFICOS– 812EE •
Faculdade de Filosofia Ciência e Letras "Tibiriçá".* Professor de Matemática da Faculdade de Administração e Ciências Contábeis "Tibiriçá".* Professor de Matemática do Colégio de São Bento ‐ São Paulo.* Professor de Matemática por concurso do Ensino Oficial do Estado de São Paulo. •
Noriyasu Omote. Autoria Especializada em Física (conteúdos: Laboratório Virtual, Teoria, Mapa Interativo, Avaliação e Guia do Professor). Graduação em Ciências Exatas pelo Instituto de Física da USP. Especialização em Tecnologia de Ensino de Física. Autor e docente de cursos ministrados de Ciências do Ensino Fundamental e Física do Ensino Médio, Pesquisa e Desenvolvimento em Física Experimental de baixo custo (IFCE). Diretor Executivo do Instituto Galileo Galilei para a Educação (IGGE).