UNIVERSIDADE FEDERAL DO RIO DE JANEIRO

UF R J - INSTITUTO DE BIOFÍSICA CARLOS CHAGAS FILHO
MÉTODOS MATEMÁTICOS EM BIOLOGIA -2011/2
1. Um técnico de laboratório consegue preparar um meio para cultura de certa bactéria
à razão de 550cm2 por semana. Ao começar a trabalhar, o meio já contava com uma
área de 800cm2.A bactéria se multiplica neste meio de forma exponencial. No inicio
do trabalho do técnico, 80cm2 do meio já se encontravam cobertos pelas bactérias
que se multiplicam de forma tal que, a cada semana, a área coberta pela colônia
duplica-se. Pergunta-se, depois de quantas semanas a área do meio estará coberto
pelas bactérias?
Resposta
Temos a situação envolvendo duas funções distintas que dependem da mesma
variável, no caso, o tempo, medido em semanas. Uma função dá conta do trabalho
do técnico de preparar o meio, expresso em termos da área que ele consegue
preparar por semana, esta função designamos f(t) e será expressa por.
f (t )  550t  800 . A outra função dá conta do crescimento da bactéria, expresso em
termos da área de cobertura que as bactérias conseguem promover por semana:
g(t), dada por g (t )  802t . A questão do problema é saber em qual tempo a área
preparada do meio pelo técnico estará completamente coberta por bactérias Ou,
seja, quando os valores das duas funções forem o mesmo, i. e., f (t )  g (t ) .
Portanto:
f (t )  g (t )  550t  800  80  2t
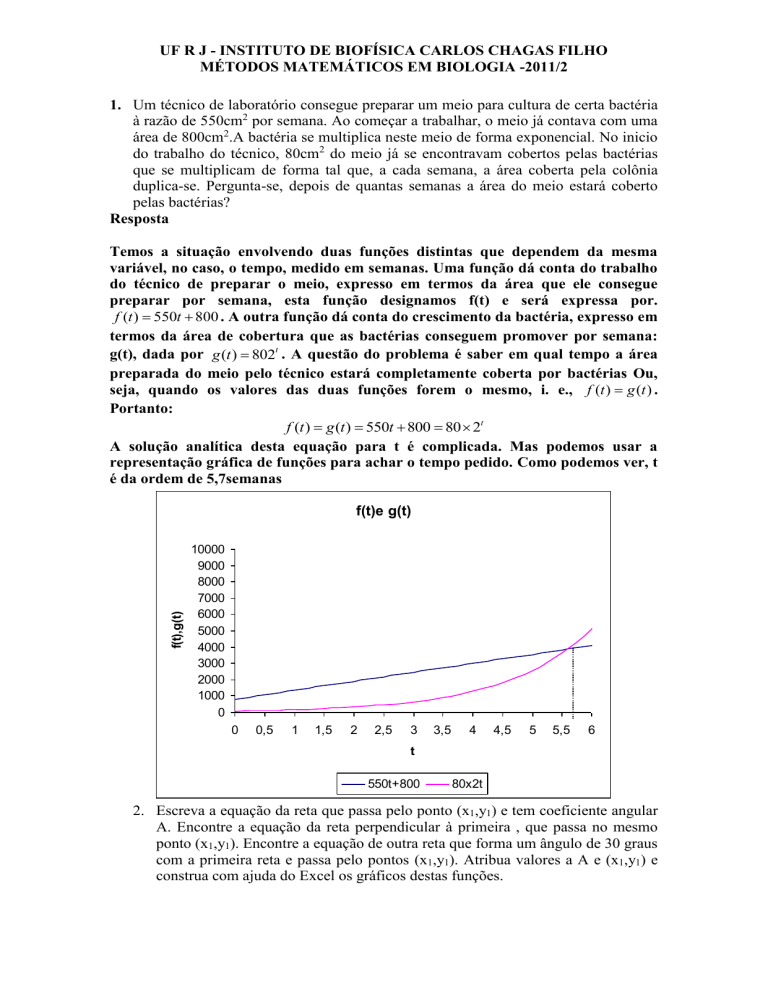
A solução analítica desta equação para t é complicada. Mas podemos usar a
representação gráfica de funções para achar o tempo pedido. Como podemos ver, t
é da ordem de 5,7semanas
f(t),g(t)
f(t)e g(t)
10000
9000
8000
7000
6000
5000
4000
3000
2000
1000
0
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
t
550t+800
80x2t
2. Escreva a equação da reta que passa pelo ponto (x1,y1) e tem coeficiente angular
A. Encontre a equação da reta perpendicular à primeira , que passa no mesmo
ponto (x1,y1). Encontre a equação de outra reta que forma um ângulo de 30 graus
com a primeira reta e passa pelo pontos (x1,y1). Atribua valores a A e (x1,y1) e
construa com ajuda do Excel os gráficos destas funções.
UF R J - INSTITUTO DE BIOFÍSICA CARLOS CHAGAS FILHO
MÉTODOS MATEMÁTICOS EM BIOLOGIA -2011/2
3. A parábola y  ( x  2)2  3 desenvolve-se inteiramente nos 1º. e 2º quadrantes
de um sistema cartesiano. Em que ponto colocamos um outro sistema cartesiano
de forma que esta parábola passe a ter seu vértice na origem deste novo sistema?
Esta manobra gráfica equivale a que transformações de variáveis realizadas na
função original?
4. Escreva a representação analítica das funções mostradas nos gráficos abaixo.
5. A seguir são dadas algumas funções correspondentes a curvas bem
características em coordenadas polares. Utilize as relações de transformação
entre os sistemas cartesiano e de coordenadas polares para traçar os respectivos
gráficos com a ajuda do Excel.
Rosa:   sen(2 )
UF R J - INSTITUTO DE BIOFÍSICA CARLOS CHAGAS FILHO
MÉTODOS MATEMÁTICOS EM BIOLOGIA -2011/2
Cardióide:   1  cos 
Caracol:  
1
 cos 
2
Lemniscata:  2  16cos 2
Nefroide de Freeth:   1  2 sen

2
Concoide de Nicómenes:   2sec   3
Cisoide de Diocles:   2sen tg
Parábola:  
8
2  2sen
Espiral Arquimedes:   