O método de Newton para a obtenção de uma raiz de uma função

O método de Newton para a obtenção de uma raiz de uma função
A raiz 𝑥̅ de uma função y = f(x), também chamada zero da função, é um número
real que anula essa função, isto é, f(𝑥̅ ) = 0.
Métodos diretos, quando podem ser aplicados, fornecem o valor exato da raiz da
equação. Esse é o caso da fórmula para a obtenção da raiz de uma equação do segundo
grau ax2 + bx + c = 0 (𝑥̅ =
−𝑏±√𝑏2 −4𝑎𝑐
2𝑎
). Também usamos um método direto para
encontrar a raiz da equação 𝑒 𝑥 − 5 = 0 (𝑒 𝑥 = 5 → 𝑥̅ = 𝑙𝑛5). O método de Newton
fornece uma ótima aproximação para a obtenção de raízes de funções quaisquer.
Vimos que a derivada de uma função y = f(x) em ponto x0 é o coeficiente
angular da reta tangente a essa curva no ponto T(x0, f(x0)). Assim, mt = f’(x0) e a reta
tangente tem equação y – f(x0) = f’(x0).(x – x0) ou então:
𝑡: 𝑦 = 𝑓 ′ (𝑥0 ). 𝑥 − 𝑓 ′ (𝑥0 ). 𝑥0 + 𝑓(𝑥0 )
Vamos usar essa interpretação geométrica da derivada para, a partir de uma
aproximação x0 para a raiz 𝑥̅ , construir uma sequência de pontos {𝑥𝑛 } = { x1, x2, x3, ... }
que converge para essa raiz 𝑥̅ .
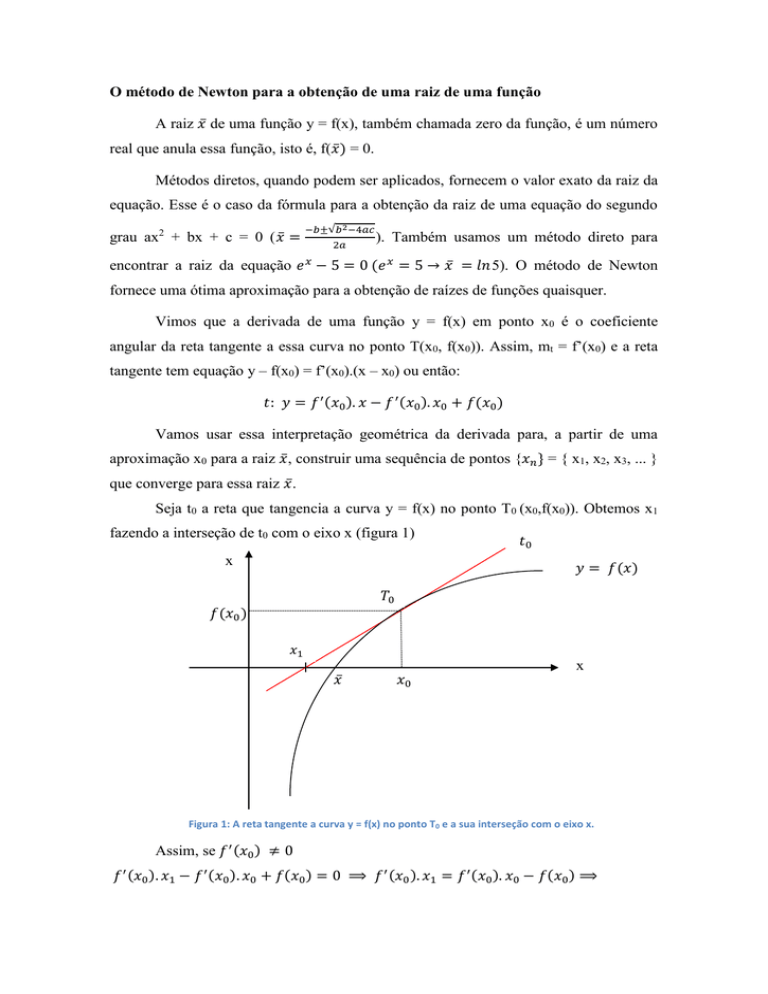
Seja t0 a reta que tangencia a curva y = f(x) no ponto T0 (x0,f(x0)). Obtemos x1
fazendo a interseção de t0 com o eixo x (figura 1)
x
𝑡0
𝑦 = 𝑓(𝑥)
𝑇0
𝑓(𝑥0 )
𝑥1
𝑥̅
𝑥0
x
Figura 1: A reta tangente a curva y = f(x) no ponto T0 e a sua interseção com o eixo x.
Assim, se 𝑓 ′ (𝑥0 ) ≠ 0
𝑓 ′ (𝑥0 ). 𝑥1 − 𝑓 ′ (𝑥0 ). 𝑥0 + 𝑓(𝑥0 ) = 0 ⟹ 𝑓 ′ (𝑥0 ). 𝑥1 = 𝑓 ′ (𝑥0 ). 𝑥0 − 𝑓(𝑥0 ) ⟹
𝑥1 = 𝑥0 −
𝑓(𝑥0 )
𝑓 ′ (𝑥0 )
Obtemos os demais pontos da sequência repetindo o procedimento, isto é:

traçamos a reta t1 que tangencia a curva y = f(x) em T1 (x1,f(x1)). Fazendo a
interseção de t1 com o eixo x obtemos x2.
𝑥2 = 𝑥1 −

𝑓(𝑥1 )
𝑓 ′ (𝑥1 )
traçamos a reta t2 que tangencia a curva y = f(x) em T2 (x2,f(x2)). Fazendo a
interseção de t2 com o eixo x obtemos x3.

E assim sucessivamente (figura 2), encontramos
𝑥𝑘+1 = 𝑥𝑘 −
𝑓(𝑥𝑘 )
𝑓 ′ (𝑥𝑘 )
𝑡2
y
𝑡1
𝑡0
𝑦 = 𝑓(𝑥)
x
𝑓(𝑥0 )
𝑇0
𝑥1
x
𝑓(𝑥2 )
𝑥2 𝑇2
𝑓(𝑥1 )
𝑇1
𝑥0
x
̅
Figura 2: A construção da sequência {xn} que converge para 𝒙
Uma pergunta importante: Essa sequência {xn} sempre converge para a raiz 𝑥̅ ? E
quando devemos considerar 𝑥𝑛 = 𝑥̅ ?
𝑓(𝑥).𝑓"(𝑥)
|
[𝑓 ′ (𝑥)]2
A resposta à primeira pergunta é dada pelo teorema: Se |
< 1 para
qualquer x em um intervalo em torno de uma raiz 𝑥̅ , a sequência {xn} construída pelo
método de Newton converge para 𝑥̅ qualquer que seja o valor inicial de x0 nesse
intervalo (Finney, Weir e Giordano - Cálculo: George B Thomas, volume 1).
Em outras palavras o teorema diz que se escolhermos x0 suficientemente
próximo da raiz 𝑥̅ e tal que f”(x0) ≠ 0, então a sequência {xn} muito provavelmente vai
convergir para a raiz 𝑥̅ . Há exceções, mas são poucas.
Para a segunda questão consideramos xn = 𝑥̅ quando |f(xn)| é próximo de zero.
Para tanto estabelecemos uma precisão ε e consideramos 𝑥𝑘 = 𝑥̅ quando |f(xk)| < ε
Observação: As operações para a construção {xn} são trabalhosas. Devemos,
preferencialmente, usar uma planilha eletrônica para a aplicação do Método de Newton.
A localização da raiz - e a conseqüente escolha da aproximação inicial x0 - pode ser
feita a partir da construção do gráfico da função. Usamos o Excel para o exemplo
abaixo.
Ex 1. Encontrar a raiz de x3 – x – 1 = 0, considerando ε = 10-6.
y
O gráfico da função, desenhado com o Winplot,


mostra que temos uma única raiz e que ela está

entre x = 1 e x = 2.

x









Observar também que f(1) = -1 < 0 e que f(2) = 5
> 0. Vamos considerar x0 = 1,5.


Como f ’(x) = 3x2 – 1, a sequência é construída a

partir de 𝑥𝑘+1 = 𝑥𝑘 −

𝑥𝑘 3 − 𝑥𝑘 −1
3𝑥𝑘 2 −1
e mostrada na
planilha abaixo:
Ex. 2: Encontrar a raiz de √𝑥 − 2𝑥 + 2 = 0, considerando ε = 10-6. Desenhar o gráfico
com o winplot.
Ex. 3: Encontrar o ponto de interseção entre as curvas y = e-x e y = 2x+1. Observe que
esse ponto de interseção é a raiz da equação e-x – (2x+1) = 0. Desenhar o gráfico com o
winplot. Considerar ε = 10-6.
Ex. 3: Idem para y = ln(1 – x2) e y = x -1. Considerar ε = 10-9.
2
Ex. 4: Idem para 𝑦 = 𝑒 −𝑥 e y = x2 – x + 1, Considerar ε = 10-9.