INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SÃO PAULO

INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SÃO PAULO
CAMPUS “SÃO PAULO”
FÍSICA EXPERIMENTAL
ENGENHARIA DE CONTROLE E AUTOMAÇÃO
DETERMINAÇÃO DE VELOCIDADE PÓS COLISÃO
SÃO PAULO
2015
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SÃO PAULO
CAMPUS “SÃO PAULO”
MORGANA MADEIRA
RAPHAEL YOSHIKAZU OSAKI
ROGÉRIO GRACINO DA SILVA JÚNIOR
FÍSICA EXPERIMENTAL
ENGENHARIA DE CONTROLE E AUTOMAÇÃO
DETERMINAÇÃO DE VELOCIDADE PÓS COLISÃO
Trabalho apresentado ao Instituto Federal
de São Paulo, como parte dos relatórios
de Física Experimental I, do curso de
Engenharia de Controle e Automação.
SÃO PAULO
2015
1. OBJETIVO
Determinar a velocidade final de uma corpo após uma colisão elástica sem utilizar
medição de períodos ou intervalos de tempo.
2. INTRODUÇÃO
A quantidade de movimento linear ou simplesmente momento linear é uma grandeza
vetorial que considera a velocidade e a quantidade de matéria que está se movendo,
com o módulo desta grandeza sendo:
⃗ = 𝑚 . 𝑣 [𝑘𝑔. 𝑚⁄𝑠]
𝑄
Considerando também o teorema do impulso que relaciona uma força aplicada em
um determinado tempo:
𝐹 = 𝑚.𝑎 ∴ 𝐹 = 𝑚
⃗⃗⃗⃗
∆𝑣
⃗𝐹 −𝑄
⃗ 𝐼 ∴ 𝑰 = ∆𝑸
⃗⃗
∴ 𝐹 . ∆𝑡 = 𝑚 . ⃗⃗⃗⃗⃗⃗
∆𝑣 ∴ 𝐼 = 𝑚𝑣 − 𝑚𝑣0 ∴ 𝐼 = 𝑄
∆𝑡
Com o impulso é a variação da quantidade de movimento, se não houver ação de
forças externas, não haverá impulso, proporcionando a conservação da quantidade de
movimento, esse processo ocorre em colisões, explosões e disparos de arma de fogo.
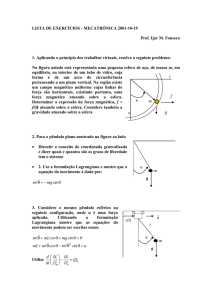
Assim considerando uma colisão em que um corpo em repouso sofre o impacto da
batida de outro corpo que estava em movimento, a quantidade inicial de momento linear
deverá ser igual à quantidade final, em que possivelmente ambos os corpos poderão
estar se movendo, conforme a figura 1.
Figura 1. Colisão elástica com um corpo em repouso
A partir do conceito de conservação da quantidade de movimento, podemos deduzir
que a o momento linear inicial é igual ao final e como comumente não há variação da
massa dos corpos, o que sofre modificação durante a colisão são as velocidades.
⃗⃗⃗⃗
𝑄𝐼 = ⃗⃗⃗⃗⃗
𝑄𝐹 ∴ 𝑚𝐴 𝑣𝐴 + 𝑚𝐵 𝑣𝐵 = 𝑚𝐴 𝑣𝐴 ′ + 𝑚𝐵 𝑣𝐵 ′ (1)
No entanto, a determinação de tais velocidades necessitam de equipamentos de
alta performance para exibir os dados exatidão, buscando dimensionar tais velocidade
podem ser usados sistemas distintos acoplados a cada um dos corpos como o conceito
da conservação de energia mecânica de uma esfera ao descer uma rampa e a
velocidade linear de um corpo em um arranjo de pêndulo simples.
Um corpo em repouso posicionado no ponto mais alto de uma rampa, possui a
energia potencial gravitacional máxima dentre as possíveis sobre este plano e assim
energia cinética mínima (zero) por estar em equilíbrio estático, enquanto no outro
extremo da rampa, a energia gravitacional é nula, enquanto a energia cinética é máxima.
(𝟏) 𝑬𝒊 = 𝒎𝒈𝒉
(𝟐) 𝑬𝒇 =
𝒎𝒗𝟐
𝟐
Considerando o conceito de conservação de energia mecânica, tal energia inicial é
igual a final. Assim, isolando a velocidade em que o corpo se encontra no final da rampa:
𝐸𝑖 = 𝐸𝑓 ∴ 𝑚𝑔ℎ =
𝑚𝑣²
𝑚𝑣²
∴ 𝑚𝑔ℎ =
∴ 2𝑔ℎ = 𝑣 2 ∴ 𝒗 = √𝟐𝒈𝒉 (𝟑)
2
2
Tal modelo teórica considera o corpo como uma partícula pontual, desconsiderando
a energia perdida no movimento de rotação do objeto. Ao considerar a energia de
rotação a energia mecânica final será igual à soma da energia de translação do centro
de massa e a energia de rotação do corpo, assim:
(𝟒) 𝑬𝒇 =
𝒎𝒗𝟐 𝑰 𝝎𝟐
𝟐
𝒗
(𝟓) 𝑰 = 𝒎𝒓𝟐 (𝟔) 𝝎 =
+
𝟐
𝟐
𝟓
𝒓
Assim a energia de rotação será:
2
2
𝑣²
2
2
2 𝑣
𝑚𝑟 2
𝑚𝑣² 2𝑚𝑣² 𝒎𝒗²
𝐼 𝜔² 5 𝑚𝑟 ( 𝑟 )
5
𝑟²
=
=
= 5
=
=
(𝟕)
2
2
2
2
10
𝟓
Com isso a energia mecânica ao final da rampa será:
𝐸𝑓 =
𝑚𝑣² 𝑚𝑣²
𝟕𝒎𝒗²
+
∴ 𝑬𝒇 =
(𝟖)
2
5
𝟏𝟎
Igualando a energia inicial (1) a final do segundo modelo (8), visando a hipótese de
conservação da energia mecânica e isolando a velocidade:
𝐸𝑖 = 𝐸𝑓 ∴ 𝑚𝑔ℎ =
7𝑚𝑣²
10𝑔ℎ
𝟏𝟎𝒈𝒉
∴ 10𝑔ℎ = 7𝑣 2 ∴ 𝑣 2 =
∴𝒗=√
(𝟗)
10
7
𝟕
Assim ao utilizar o segundo modelo teórico o dimensionamento da velocidade do
corpo ao final da rampa se torna mais fiel.
Já pêndulo simples é um dispositivo formado por um fio inextensível, com um corpo
de massa m acoplado a um fio sem massa e inextensível suspenso com comprimento
L, que quando deslocado em relação à posição de equilíbrio e em seguida abandonado,
oscilará com amplitude A, conforme a figura 1.
Figura 1. Pêndulo Simples.
Ao sofrer um impacto, ocorre o deslocamento do corpo da posição de repouso
(0) até certa amplitude, promovendo a realização de um movimento oscilatório.
Desconsiderando a resistência do ar, após o impacto as únicas forças atuantes sobre o
pêndulo serão a tensão do fio inextensível e o peso gravitacional sobre o corpo de
massa m, como ilustrado na figura 2 abaixo.
Figura 2. Diagrama de forças atuantes no corpo.
Com a análise visual das forças é possível verificar que a força tração (T) exercida
pelo fio anula-se com a componente no eixo y da força peso, deste modo a única força
atuante no corpo é a componente no eixo x da força peso (PX).
Portanto a força de restauração responsável por reestabelecer o corpo na posição
de repouso será igual a componente da força peso restante.
𝐹𝑜𝑟ç𝑎 𝑑𝑒 𝑟𝑒𝑠𝑡𝑎𝑢𝑟𝑎çã𝑜 = 𝑚𝑔. 𝑠𝑒𝑛𝜃 (10)
Em experimento em que a amplitude do movimento oscilatório é extremamente
pequena em relação a largura do fio, convenciona-se que o arco formado pelo
movimento do corpo será aproximado a um segmento de reta, sobre o qual o eixo x é
fixado. Assim a partir da aproximação do arco de circunferência ocorre a formação de
um triângulo retângulo que nos permite escrever a igualdade contida na figura 3.
Figura 3. Aproximação do arco de circunferência em reta.
Aplicando esta nova relação a equação da força de restauração, com sinal negativo
por ter sentido inverso ao do eixo x:
𝐹 = 𝑚𝑔.
𝑥
𝑚𝑔
𝑜𝑢 𝐹 = − ( ) . 𝑥
𝐿
𝐿
Sabendo-se que em movimentos harmônicos simples (MHS), a força de
restauração e o período são dados por:
𝐹 = −𝑘𝑥 (11)
𝑒
𝑇 = 2𝜋√
𝑚
(12)
𝑘
Assim igualando a força de restauração do movimento harmônico ao do componente
do peso no pêndulo:
𝑚𝑔
𝑚𝑔
−𝑘𝑥 = − ( ) . 𝑥 ∴ 𝑘 =
(13)
𝐿
𝐿
Que ao substituir na equação responsável pelo período em movimento harmônico
simples (12) proporcionará uma relação entre o comprimento do fio, o período de
oscilação:
𝑚
𝑳
𝑇 = 2𝜋√ 𝑚𝑔 ∴ 𝑻 = 𝟐𝝅√ (𝟏𝟒)
𝒈
𝐿
Como o movimento harmônico simples possui o funcionamento do movimento
circular a velocidade linear do corpo na extremidade do pêndulo será dada pelo produto
entre a velocidade angular e o comprimento do fio (raio da circunferência):
𝒗 = 𝝎𝑳 (𝟏𝟓)
Com a velocidade angular determinada pela divisão da variação do deslocamento
angular pela variação do período:
𝝎=
∆𝜽
(𝟏𝟔)
𝑻
Realizando a substituição até dimensionar a velocidade linear a partir do
deslocamento angular e do comprimento do fio:
𝑣 = 𝜔𝐿 ∴ 𝑣 =
∆𝜃
𝐿∴𝒗=
𝑇
∆𝜽
𝑳
𝟐𝝅√𝒈
𝑳
A partir das equações supramencionadas, pode-se verificar a velocidade final de um
corpo que desceu uma rampa até colidir com um pêndulo simples, conforme o arranjo
experimental da figura 2. abaixo:
Figura 2. Colisão elástica com rampa e pêndulo simples
⃗⃗⃗⃗
𝑄𝐼 = ⃗⃗⃗⃗⃗
𝑄𝐹 ∴ 𝑚𝐴 𝑣𝐴 + 𝑚𝐵 𝑣𝐵 = 𝑚𝐴 𝑣𝐴 ′ + 𝑚𝐵 𝑣𝐵 ′
10𝑔ℎ
∆𝜃
𝑚𝐴 √
= 𝑚𝐴 𝑣𝐴′ + 𝑚𝐵
𝐿∴
7
𝐿
2𝜋√𝑔
𝒗′𝑨 = √
𝟏𝟎𝒈. 𝒉
𝒎𝑩 . ∆𝜽. 𝑳
−
𝟕
𝑳
𝟐𝝅. 𝒎𝑨 . √𝒈
3. MATERIAIS










Aplicativo “Transferidor – ON PROTRACTOR”;
Balança semi-analítica;
Cano de PVC curvo;
Elástico;
Escalímetro;
Esferas;
Fita adesiva;
Nível;
Suporte para o cano;
Suporte para o pêndulo.
4. PROCEDIMENTOS
Primeiramente verificou-se o alinhamento do cano de PVC curvo afixado no suporte
utilizando o nível para obter certificação do posicionamento do sistema no eixo
horizontal. Então utilizou-se o escalímetro para realizar a medição da altura entre as
extremidades do cano (h) e a base, além do comprimento do fio utilizado no pêndulo, e
a balança semi-analítica para a pesagem das esferas a serem utilizadas.
Em seguida posicionou-se o pêndulo simples a frente da rampa em que a esfera A
despencará. Após a montagem do arranjo experimental conforme a figura 3. foi
posicionado um telefone móvel com o sistema operacional android munido do aplicativo
“Transferidor – ON PROTRACTOR” que seria responsável pela medição do
deslocamento angular da esfera, logo em seguida o corpo A de massa mA foi solto, de
uma certa altura h, que a uma velocidade vA colidiu com um corpo B de massa mB em
repouso, gerando movimento harmônico simples no pêndulo, durante o primeiro período
de oscilação necessitou-se verificar o deslocamento angular da esfera através do
aplicativo, anotando-o.
Figura 3. Arranjo experimental.
5. RESULTADOS
Inicialmente verificou-se a massa das esferas utilizando uma balança semi-analítica,
inclusive a contida no sistema do pêndulo, conforme a tabela 1.
Tabela 1. Massa das esferas
Esfera do pêndulo
0,0730998 kg
Lançamento da esfera A
Esfera A
0,1118751 kg
Esfera B
0,0549814
Posicionando a esfera A de massa 0,118751 kg no ponto mais alto do cano
conforme o esquema contido na figura 4.
Figura 4. Arranjo Experimental A
Deste modo para calcular a velocidade final da esfera A após a colisão, utilizou-se
o aplicativo “Transferidor – ON PROTRACTOR”, resultando em um valor de
deslocamento angular (∆𝜃) de 92,76° o equivalente a 0,5153π.
10𝑔. ℎ
𝑚𝐸 . ∆𝜃. 𝐿
10.9,78.0,15 0,073 . 0,5153𝜋 .0,14
𝑣𝐴′ = √
−
∴ 𝑣𝐴′ = √
−
7
7
𝐿
0,14
2𝜋. 𝑚𝐴 . √𝑔
2𝜋. 0,111. √9,78
𝒗′𝑨 = 𝟏, 𝟐𝟓𝟎𝟔 𝒎/𝒔
Lançamento da esfera B
Posicionando a esfera B de massa 0, 0549814kg no ponto mais alto do cano
conforme o esquema contido na figura 5.
Figura 5. Arranjo Experimental A
Deste modo para calcular a velocidade final da esfera A após a colisão, utilizou-se
o aplicativo “Transferidor – ON PROTRACTOR”, resultando em um valor de
deslocamento angular (∆𝜃) de 129,64° o equivalente a 0,7202π.
10𝑔. ℎ
𝑚𝐸 . ∆𝜃. 𝐿
10.9,78.0,15 0,073 . 0,70,2𝜋 .0,14
𝑣𝐴′ = √
−
∴ 𝑣𝐴′ = √
−
7
7
𝐿
0,14
2𝜋. 𝑚𝐵 . √𝑔
2𝜋. 0,0,0549. √9,78
𝒗′𝑨 = 𝟎, 𝟖𝟖𝟕𝟒𝒎/𝒔
6. CONCLUSÃO
A grande vantagem de não utilizar medições de tempo ou período, é a diminuição
frente as incertezas inerentes a essas medidas, utilizando sistemas de conservação de
energia mecânica em uma rampa e conceitos de pêndulo simples, evitou-se esse tipo
de dimensionamento, baseando os dados coletados apenas em pesagens e medições
com escalímetro e a verificação do deslocamento angular através de um aplicativo para
celular, muito mais precisos que a cronometragem manual por exemplo.
Assim através dos arranjos experimentais foi possível verificar que com o aumento
da massa da esfera A (que desce a rampa), a sua velocidade após a colisão também
elevará seu valor, pois a velocidade desta esfera ao final da rampa também será maior.
Enquanto a velocidade inicial no pêndulo continuará nula.
Experimentos similares são utilizados em estudos balísticos, para determinação da
velocidade do projetil no seu disparo, assim como em outras inúmeras aplicações. Deste
modo a determinação da velocidade em sistema parecidos aos supracitados são de
grande importância quando inviabilizada a checagem dos intervalos de tempo em dados
experimentos.
7. BIBLIOGRAFIA
TIPLER, P. A.; MOSCA, G. Física para Cientistas e Engenheiros. Volume 1. 6ª Edição.
2009 – LTC
HALLIDAY, D.; RESNICK, R. Fundamentos da Física. Volume 1. 6° Edição. 2012 - LTC