Triângulos - WordPress.com

TRIÂNGULOS.
DEFINIÇÃO
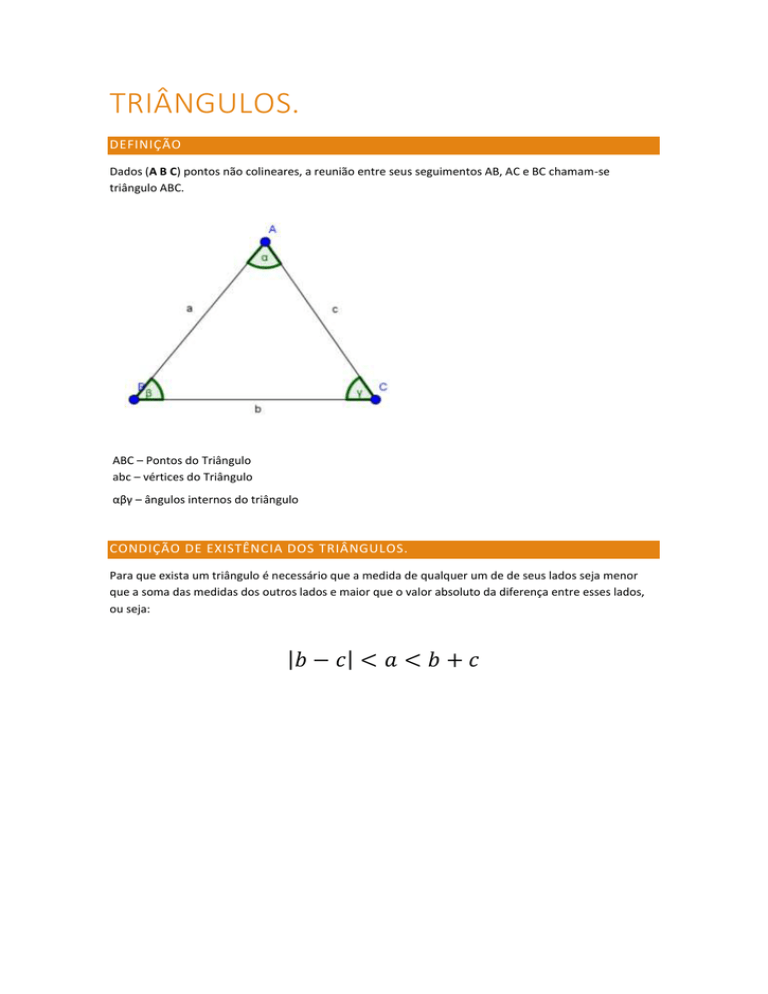
Dados (A B C) pontos não colineares, a reunião entre seus seguimentos AB, AC e BC chamam-se
triângulo ABC.
ABC – Pontos do Triângulo
abc – vértices do Triângulo
αβγ – ângulos internos do triângulo
CONDIÇÃO DE EXISTÊNCIA DOS TRIÂNGULOS.
Para que exista um triângulo é necessário que a medida de qualquer um de de seus lados seja menor
que a soma das medidas dos outros lados e maior que o valor absoluto da diferença entre esses lados,
ou seja:
|𝑏 − 𝑐 | < 𝑎 < 𝑏 + 𝑐
TEOREMA SOMA DOS ANGULOS INTERNOS E EXTERNOS
Dadas duas retas paralelas r e s, vamos usar elas de suporte para a construção do nosso triângulo.
Agora vamos fazer o nosso triângulo e seus ângulos interno e um ângulo externo.
Agora vamos utilizar as propriedades envolvidas quando temos duas retas paralelas interceptadas por
uma transversal, vamos prolongar os seguimentos de reta do meu triângulo e assim vamos usar um
outro caso que são os ângulos opostos pelo vértice.
Usando ângulos opostos pelo vértice, mais as propriedades de paralelismo, eu chego a uma equação
onde, 𝛼 + 𝛽 + 𝛾 = 360°, ou seja observamos que a soma dos ângulos internos de um triângulo é de
180 graus.
Agora vamos ver o que acontece no nosso ângulo externo δ
Observamos que aqui temos que 𝛾 + 𝛿 = 180°, assim partindo da demonstração dada anteriormente,
temos que 𝛾 + 𝛿 = 𝛼 + 𝛽 + 𝛾 , tendo γ em comum em ambos os lados eu chego a essa equação, onde:
𝛿 =𝛼+𝛽
Então, podemos observar que para achar o valor do ângulo externo e somente fazer a soma dos outros
ângulos do meu triângulo.
Assim então temos que: 𝛼 + 𝛽 + 𝛾 = 360° e 𝛿 = 𝛼 + 𝛽.
CLASSIFICAÇÃO DOS TRIÂNGULOS
Os ângulos eles são classificados de acordo com a tabela abaixo.
ce
les
len
o
Isó
Es
ca
Ac
ut
ân
gu
lo
Re
tu
tâ
sâ
ng
ng
ulo
ulo
Â
N
G
U
L
O
Ob
L
A
D
O
Eq
uil
áte
r
o
Classificação dos Triângulos
3 Lados Iguais
3 Angulos Iguais
2 Lados Iguais
2 Ângulos iguais
3 Lados Diferentes
3 Ângulos Diferentes
3 Ângulos agudos
1 ângulo reto
2 ângulos Agudos
1 Ângulo Obtuso
2 Angulos Agudos
MEDIANA DE UM TRIÂNGULO E BARICENTRO
Mediana
A mediana, é um segmento de reta que parte do vértice ao ponto médio do lado oposto ao vértice.
O seguimento de reta BM, parte do vértice B e intercepta o segmento de reta AC no seu ponto médio
M, dividindo em dois segmentos de reta congruentes AM e MC.
Baricentro
As três medianas do triângulo, se interceptam em um mesmo ponto que divide cada mediana em duas
partes tais que a parte que contém o vértice é o dobro da outra.
Assim então observamos que o ponto G, é o ponto aonde as medianas se interceptam. Usando a
mediana CN, observamos que o ponto G se encontra em
2
3
da semirreta CN, ou seja
2
𝐺 = 𝐶𝑁
3
O baricentro, leva esse nome de ponto G, pois ele é o centro de gravidade do triângulo.
BISSETRIZ E INCENTRO
Bissetriz
É o segmento de reta que vai do vértice, onde divide seu ângulo em dois ângulos congruentes tocando o
lado oposto do vértice.
O segmento de reta formado por AS, podemos observar que ele dividiu o ângulo do vértice A em dois
ângulos α e foi para o segmento de reta BC.
Incentro.
As três bissetrizes do triângulo se interceptam em um mesmo ponto. Este ponto ele fica a uma mesma
distância dos lados do meu triângulo. Essa distância é o raio da minha circunferência inscrita no
triângulo, por isso esse ponto leva o nome de incentro, pois ele fica no centro de uma circunferência.
MEDIATRIZES E CIRCUNCENTRO
Mediatrizes
É o segmento de reta que parte do ponto médio do lado de um triangulo ao lado oposto.
Circuncentro
As mediatrizes dos lados do triangulo, elas se interceptam em um mesmo ponto. Este ponto ele está
igual a distância do vértices do triangulo, assim podendo dizer que essa distância é o raio da minha
circunferência circunscrita no triangulo, logo o meu circuncentro é o centro da circunferência
circunscrita no triangulo.
ORTOCENTRO
É o ponto onde as três retas suportes da altura do triangulo se encontram. Isto é as retas traçadas dos
vértices do triângulo chegando aos seus lados opostos em perpendicularidade, ou seja em um ângulo
reto. O nome orto, deriva do grego que quer dizer reto, dando uma referência do ângulo formado entre
a base e a altura
.
Fonte das imagens em pesquisa no google.com, algumas fontes vem do livro
fundamentos de matemática elementar volume 9 de Osvaldo Dolce e José Nicolau
Pompeo.