12) A vida útil de certo componente eletrônico é, em média, 10.000

EXERCÍCIOS PROPOSTOS - AVALIAÇÃO 2
VARIÁVEIS ALEATÓRIAS, DISTRIBUIÇÕES
INTERVALOS DE CONFIANÇA
DE
PROBABILIDADE,
DISTRIBUIÇÕES
AMOSTRAIS
E
1) Apresente a função de probabilidade para as seguintes variáveis aleatórias:
a) Número de caras obtido com o lançamento de uma moeda honesta.
b) Número de caras obtido no lançamento de duas moedas honestas.
c) Número de peças com defeito em uma amostra de duas peças, sorteadas aleatoriamente de um
grande lote, em que 40% das peças são defeituosas.
d) Número de peças com defeito em uma amostra de três peças, sorteadas aleatoriamente de um
grande lote, em que 40% das peças são defeituosas.
e) Apresente a função de probabilidade acumulada do item d.
f) Calcule os valores esperados e as variâncias das distribuições de probabilidade dos itens a e c.
a)
x
0
1
P(x)
0,5
0,5
b)
x
0
1
2
P(x)
0,25
0,5
0,25
c)
x
0
1
2
P(x)
0,36
0,48
0,16
d)
x
0
1
2
3
e)
P(x)
0,216
0,432
0,288
0,064
ì0 se x < 0
ï
ïï0, 261 se 0 £ x < 1
f (x) = í0, 648 se 1 £ x < 2
ï0, 936 se 2 £ x < 3
ï
îï1 se x ³ 3
f)
Item a:
0,5 e 0,25
Item c:
0,8 e 0,48
2) Seja X uma variável aleatória com função de distribuição acumulada dada por
ì1- e- x se x ³ 0
. Obtenha a função densidade de probabilidade de x.
F(x) = í
î0 se x < 0
ìe- x se x ³ 0
f (x) = í
î0, se x < 0
ì x se 0 £ x < 1
ï
3) Seja X com função densidade de probabilidade dada por f (x) = í2 - x se 1 £ x < 2 .
ï
î0 se x Ï [0, 2)
a) Obtenha P(0<x<1) 1/2
b) Obtenha P(1/3<x<3/2) 59/72
c) E(X) 1
d) V(X) 1/6
4) Suponha que 10% dos clientes que compram a crédito em uma loja deixam de pagar
regulamente suas prestações. Se num particular dia, a loja vende a crédito para 10 pessoas, qual é
a probabilidade de que mais de 20% delas deixem de pagar regularmente as contas? Suponha que
as 10 pessoas que fizeram crediário nesse dia correspondam a uma amostra aleatória de clientes
potenciais desta loja.
R: 0,0702
5) Em um sistema de transmissão de dados, existe uma possibilidade igual a 0,05 de um lote de
dados ser transmitido erroneamente. Foram transmitidos 20 lotes de dados para a realização de
um deste de análise da confiabilidade do sistema.
a) Calcule a probabilidade de haver erro na transmissão.
b) Calcule a probabilidade de que haja erro na transmissão em exatamente 2 dos 20 lotes de
dados.
c) Qual é o número esperado de erros no teste realizado?
R: a) 0,6415 b) 0,1886 c)1
6) Numa fábrica, 3% dos artigos produzidos são defeituosos. O fabricante pretende vender 4000
peças e recebeu duas propostas:
Proposta 1: o comprador A propõe examinar uma amostra de 80 peças. Se houver 3 ou menos
defeituosas, ele paga 60 unidades monetárias por peça; caso contrário, ele paga 30 unidades
monetárias por peça.
Proposta 2: o comprador B propõe examinar uma amostra de 40 peças. Se todas forem perfeitas,
ele paga 65 unidades monetárias por peça; caso contrário, ele paga 20 unidades monetárias por
peça.
Qual é a melhor proposta? (Calcule o valor esperado da venda em cada proposta)
R: Proposta 1
7) Placas de circuito integrado são avaliadas após serem preenchidas com chips semicondutores.
Considere que foi produzido um lote de 20 placas e selecionadas 5 para avaliação. Calcule a
probabilidade de encontrar pelo menos uma placa defeituosa, supondo que o lote tenha 4
defeituosas e que tenha sido realizada:
a) uma amostragem aleatória com reposição;
b) uma amostragem aleatória sem reposição.
R: a)0,6723 b) 0,7183
8) O número de petroleiros que chegam a uma refinaria em cada dia ocorre segundo uma
distribuição de Poisson, com l = 2. As atuais instalações podem atender, no máximo, a 3
petroleiros por dia. Se mais de 3 aportarem num dia, o excesso é enviado a outro porto. Em um
dia, qual a probabilidade de se enviar petroleiros para outro porto?
R: 0,145
9) Suponha que o número de falhas em certo tipo de placa plástica tenha distribuição de Poisson,
com taxa média de 0,05 defeito por m2. Na construção de um barco, é necessário cobrir uma
superfície de 3 m x 2 m com essa placa.
a)Qual é a probabilidade de que não haja falhas nessa superfície?
b) Qual é a probabilidade de que haja mais que uma falha nessa superfície?
R: a) 0,7408 b) 0,037
10) Suponha que os erros tipográficos na edição de um livro de 300 páginas sejam distribuídos
aleatoriamente com uma média de 1 página com erros a cada 100 páginas. Determine a
probabilidade de acharmos no livro todo:
a) nenhuma página com erros tipográficos
b) pelo menos duas páginas com erros tipográficos
c) entre 1 e 3 páginas com erros tipográficos
R: a) 0,05 b)0,80 c)0,60
11) A vida útil de certo componente eletrônico é, em média, 10.000 horas e apresenta distribuição
exponencial. Qual é a porcentagem esperada de componentes que apresentarão falhas em menos
de 10.000 horas?
R: 0,6321
12) A vida útil de certo componente eletrônico é, em média, 10.000 horas e apresenta distribuição
exponencial. Após quantas horas se espera que 25% dos componentes tenham falhado?
R: 2877 horas
13) O tempo de vida de uma lâmpada é uma variável aleatória com distribuição exponencial de
parâmetro 2. Qual é a probabilidade de a lâmpada durar:
a) menos de 2 unidades de tempo
b) pelo menos 3 unidades de tempo
c) entre 1 e 3 unidades de tempo
R: a) 0,6321 b) 0,2231 c) 0,3834
14) A temperatura de congelamento da água (0o C) foi medida em vários termômetros. O valor
médio das medidas foi μ = 0,0o C e o desvio-padrão foi σ = 1,00o C. Admita que a distribuição de
frequência dos erros se assemelhe a uma distribuição normal. Escolhido aleatoriamente um
termômetro, determine a probabilidade de que no ponto de congelamento da água o termômetro
marque
a) entre 0o C e 1,58o C;
b) entre -2,43o C e 0o C;
c) uma leitura superior a 1,27o C;
d) entre 1,2o C e 2,3o C
R: a) 0,4429 b) 0,4925 c) 0,1020 d) 0,1044
16) Na engenharia humana e no projeto de produtos, frequentemente é importante
considerarmos os pesos das pessoas, de modo que não haja sobrecarga em aviões ou elevadores,
as cadeiras não se quebrem, e não ocorram outros acontecimentos perigosos ou embaraçosos.
Dado que a população de homens tem pesos distribuídos normalmente com média de 173 lb e
desvio-padrão de 30 lb, determine a probabilidade de que um homem escolhido aleatoriamente
pese mais que 180 lb.
R: 0,4090
18) A quantidade de líquido em garrafas de um certo tipo de refrigerante tem distribuição normal
com média 1000 mL e desvio padrão 10 mL.
a) Uma garrafa é considerada dentro do padrão se apresentar conteúdo entre 990 e 1010 mL
Selecionando-se ao acaso uma garrafa desse tipo de refrigerante, qual é a probabilidade da mesma
estar dentro do padrão ?
b) Numa amostra de 500 garrafas, qual é a probabilidade aproximada de pelo menos 360 estarem
dentro do padrão?
c) Serão retiradas do mercado as garrafas com conteúdo inferior a 990mL. Qual é a probabilidade
de uma garrafa selecionada ao acaso ser retirada do mercado?
d) Numa amostra de 100 garrafas, calcule a probabilidade aproximada de que no máximo 12
sejam retiradas do mercado.
R: a)0,6826 b) 0,0367 c) 0,1587 d)0,1469
19) Considere uma população P={2,3,6,8,11}. Construa a distribuição amostral, calcule o valor
esperado e a variância e compare esses valores com a média e a variância da população
considerando duas situações:
a) Uma amostra de dois elementos com reposição será retirada aleatoriamente.
b) Uma amostra de dois elementos sem reposição será retirada aleatoriamente.
R: a) E(X) = 6 V(X) = 5, 4 b) E(X) = 6 V(X) = 4, 05
20) A distribuição dos diâmetros de parafusos produzidos por uma certa máquina é normal, de
desvio-padrão igual a 0,17 mm. Uma amostra de seis parafusos retirada ao acaso da produção
apresentou os seguintes diâmetros (em milímetros): 25,4 25,2 25,6 25,3 25,0 25,4
Construa intervalos de 90% de confiança para o diâmetro médio da produção dessa máquina.
R: 25,32 ± 0,1142
21) Uma pesquisa de quinze elementos retirada de uma população normalmente distribuída
forneceu
X = 32,4 e s2 = 2,56. Construa intervalos de 95% de confiança para a média da
população.
R: 32, 4 ± 0,8861
22) Suponha que se esteja estudando a altura de pessoas numa certa população. A amostra de
-
100 indivíduos resultou em x =170 e
populacional com
a) 90% de confiança
b) 99% de confiança
R: a) 170 ± 2, 4675 b) 170 ± 3,8625
s =15. Construa intervalos de confiança para a média
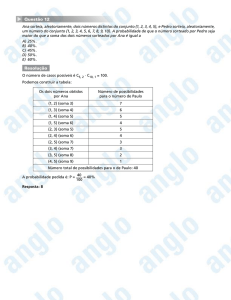
23) Suponha a seguinte amostra sobre a intenção de voto em um candidato:
1; 0; 1; 1; 1; 1; 0; 0; 1; 1; 0; 0; 0; 0; 0; 1; 0; 0; 1; 0.
Construa um Intervalo de Confiança de 98% para a proporção.
R: 0, 45± 0, 2581