Lista de Exercícios

1
Universidade Tecnológica Federal do Paraná
Campus Campo Mourão
Engenharia Eletrônica
LT34C - Circuitos Elétricos
Profa. Me. Luciane Agnoletti dos Santos Pedotti
Lista de Exercícios – P1
1) Calcule o período de uma onda cuja frequência é:
a) 25Hz
b) 35MHz
c) 1Hz
d)25kHz
2) Calcule a frequência de uma onda cujo período é:
a) 1/60s
b) 0,01s
c) 35ms
d) 25µs
3) Calcule o período de uma onda senoidal que completa 80 ciclos em 24ms
4) Converta os valores dos seguintes ângulos em graus para radianos.
a) 45°
b) 120°
c) 270°
d) 178°
5) Determine a velocidade angular da uma onda cujo período é:
a) 2s
b) 4µs
c) 0,3ms
d) 1/26s
6) Calcule a amplitude e a frequência a partir das seguintes funções:
a) 20𝑠𝑒𝑛377𝑡
b) 5𝑠𝑒𝑛754𝑡
c) 0,001𝑠𝑒𝑛942𝑡
d) −7,6𝑠𝑒𝑛43,6𝑡
7) Se 𝑣 = 40𝑉 para 𝛼 = 30° e 𝑡 = 1𝑚𝑠, determine a expressão matemática para a
tensão senoidal.
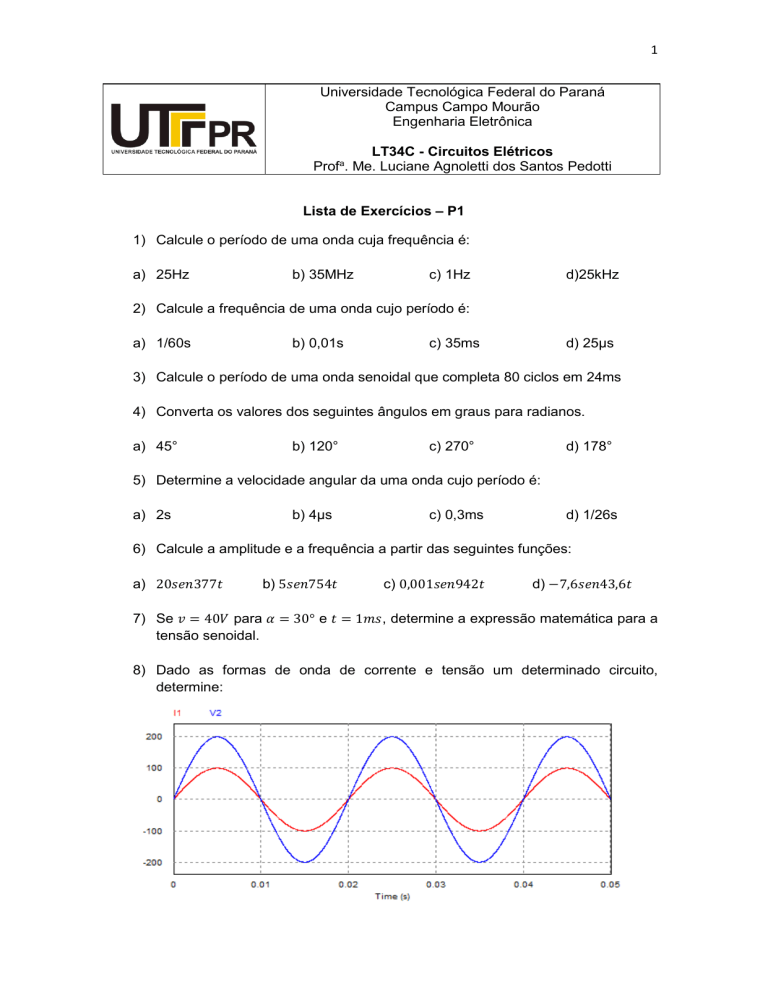
8) Dado as formas de onda de corrente e tensão um determinado circuito,
determine:
2
a) A frequência do sistema.
b) Faça a dedução da tensão eficaz do sistema.
c) Com base na dedução anterior, determine a corrente eficaz do sistema.
9) Determine a diferença de fase entre as formas de onda de cada par a seguir:
a) 𝑣 = 4𝑠𝑒𝑛(𝜔𝑡 + 50°); 𝑖 = 6𝑠𝑒𝑛(𝜔𝑡 + 40°);
b) 𝑣 = 25𝑠𝑒𝑛(𝜔𝑡 − 80°); 𝑖 = 0,005𝑠𝑒𝑛(𝜔𝑡 − 10°);
c) 𝑣 = 0,2𝑠𝑒𝑛(𝜔𝑡 − 60°); 𝑖 = 0,1𝑠𝑒𝑛(𝜔𝑡 + 20°);
10) Escreva expressões analíticas para as formas de onda das figuras abaixo com
ângulo de fase em graus.
11) Determine a reatância indutiva (em ohms) de um indutor de 2H no caso de:
a) Corrente contínua
e para as seguintes frequências:
b) 25Hz
c) 60Hz
d) 10kHz
e) 1MHz
12) Determine a frequência para a qual um indutor de 10 H apresenta as seguintes
reatâncias indutivas:
a) 50Ω
b) 3770Ω
c) 16,3Ω
d) 338Ω
13) Calcule a reatância capacitiva (em ohms) de um capacitor de 5µF em:
a) Corrente contínua
e para as seguintes frequências:
b) 120Hz
c) 60Hz
d) 1kHz
14) Determine a capacitância de um capacitor cuja reatância é:
a) 250Ω/60Hz
b) 55Ω/312Hz
c) 10Ω
/25Hz
e) 24kHz
3
15) Converta os números complexos a seguir de retangular para polar e vice-versa.
a) 4+j3
b) 5-j2
c) 7∟45º
d) 10∟55º
e) 4,5∟90º
16) Determine a resistência equivalente dos seguintes circuitos (forma polar e
retangular):
a) R1 = 10Ω ; L1 = 5mH
b) R1 = 12Ω; C1 = 35µF
c) R1 = R2 = R3 = 5Ω; L1 = L2 = L3 = 8mH
17) Represente o número complexo a seguir no plano complexo:
a) 𝑋 = 5∠30°
b) 𝑍 = 4 + 𝑗3
c) 𝑌 = 7 − 𝑗4
d) 𝑊 = −4,2∠60°
18) Represente os fasores das seguintes formas de onda:
a) 𝑣(𝑡) = 20𝑠𝑒𝑛(𝜔𝑡 + 20°); 𝑖(𝑡) = 5𝑠𝑒𝑛(𝜔𝑡)
b) 𝑣(𝑡) = 20𝑠𝑒𝑛(𝜔𝑡 + 10°); 𝑖(𝑡) = 4𝑠𝑒𝑛(𝜔𝑡 + 50°)
19) Calcule o Fator de Potência para os circuitos a seguir. Se necessário, faça a
correção do FP para 0,95 indutivo. Calcule o capacitor necessário.
a) Dados: 𝑣(𝑡) = 180𝑠𝑒𝑛(𝜔𝑡); 𝑓 = 60𝐻𝑧; R1 = 5Ω; R2 = 7Ω; R3 = 9,5Ω; L1 = 9mH;
L2 = 15mH; L3 = 6,6mH.
4
b) Dados: idem ao anterior, com 𝑓 = 50𝐻𝑧
20) Calcule todas as quedas de tensão nos elementos passivos dos circuitos
abaixo, bem como todas as correntes das malhas. Dados: 𝑣(𝑡) =
180𝑠𝑒𝑛(𝜔𝑡); 𝑓 = 60𝐻𝑧;
a) R1 = 10Ω; L1 = 5mH; C1 = 35µF
b) R1 = 10Ω; L1 = 5mH; C1 = 35µF; L2 = 7,5mH; R2 = 5Ω; C2 = 5µF
5
SISTEMA POLIFÁSICO
21) Para uma carga equilibrada com uma resistência de 10Ω por fase conectada
num gerador trifásico a quatro fios conectado em Y com uma tensão de linha
de 220V. calcule: a tensão de fase do gerador, a tensão de fase da carga, a
corrente de fase da carga, a corrente de linha da carga, determine a potência
ativa, reativa e aparente. Determine o fator de potência do circuito. Calcule o
capacitor que deve ser inserido no sistema para corrigir o fator de potência em
0,95 indutivo, caso necessário.
22) A sequência de fase do sistema da figura a seguir é ABC. Determine: os
ângulos θ1 e θ2; as tensões de fase em forma fasorial; as correntes de fase em
forma fasorial; o diagrama fasorial das correntes e demonstre que sua soma
fasorial é zero; determine as correntes de linha; determine as tensões de linha.
6
23) Utilizando transformações adequadas, obtenha a impedância trifásica equivalente
do circuito a seguir. (lembre-se: na transformação as impedâncias ficarão em
paralelo).
24) Para o sistema da figura a seguir, determine o módulo das tensões e correntes
desconhecidas. Determine a potência ativa, reativa e aparente do sistema e o
fator de potência.
25) Para o circuito a seguir, determine o módulo e o ângulo de fase das correntes
de fase e correntes de linha. Determine também o módulo e o ângulo de fase
das tensões EAB EBC ECA
7
26) Para o circuito a seguir, determine o módulo e o ângulo de fase das correntes
de fase e correntes de linha. Determine também o módulo e o ângulo de fase
das tensões EAB EBC ECA. Calcule a potência média (ativa) total, reativa e
aparente do sistema. Determine o fator de potência. É necessário corrigi-lo de
acordo com as determinações da ANEEL? Justifique.
27) Utilizando o método dos dois Wattímetros, determine a potência total no
circuito a seguir. (P, Q e S)
28) Para o sistema Y a 4 fios, determine:
a) a tensão em cada fase;
b) a corrente em cada fase;
c) A potência ativa, reativa e aparente total do sistema;
d) o fator de potência do sistema;
e) a corrente In
8
29) Para o sistema Y a 3 fios, determine:
a) a tensão em cada fase;
b) a corrente em cada fase;
c) A potência ativa, reativa e aparente total do sistema;
d) o fator de potência do sistema.