exercicios exponencial

Disciplina: MATEMÁTICA
Escola SESI de Anápolis - Jundiaí
Aluno (a):
Turma:
2º Ano
Professor (a) : CÉSAR LOPES DE ASSIS / Guilhermino Neto
Data:
RESUMO – FUNÇÃO EXPONENCIAL
Função exponencial: É qualquer função f: IR  IR da forma f(x) = ax, com a > 0 e a ≠ 1.
O crescimento exponencial em alguns casos pode ser vertiginoso; em outros momentos, pode tender
lentamente a zero, sem nunca atingi-lo. A função exponencial é fundamental para explicar numericamente
desde fenômenos biológicos até fenômenos físicos complexos, como a transmutação radioativa.
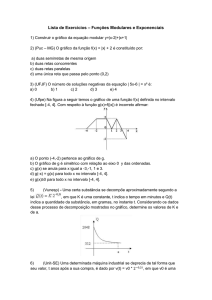
Gráficos da função exponencial: Considerando a = 2 e a =
1
, construímos os gráficos a seguir:
2
OBSERVAÇÕES:
1) Se a > 1, a função é crescente e se 0 < a < 1, a função
será decrescente.
2) Os gráfico não intersectam o eixo X, pois as funções
não se anulam, seja qual for o valor de x.
3) Os valores da função exponencial são todos positivos,
qualquer que seja x.
4) Uma desigualdade de membros positivos não se altera
quando se elevam ambos os membros ao mesmo
expoente positivo, e muda de sentido quando o expoente
é negativo:
Para x  0 : a  b  a x  b x
.

x
x
Para x  0 : a  b  a  b
5) A função exponencial de IR para IR*+. Isto é: a
x1
 a x2  x1  x 2 , para 0  a  1.
Propriedades da Potenciação: Se a e b forem números positivos e x, y reais quaisquer, então:
0
x
a) a  1 b) a  0 c) a  x 
1
x
y
xy
d) a .a  a
ax
e)
ax
 a xy
ay
 
x
f) a
y
 a x. y
x
x
g) a.b   a .b
x
Comparação entre bases de uma função exponencial: As fórmulas de cálculo ficam simplificadas quando
escolhemos para base aquela para a qual resulta uma reta tangente y  ax  b no ponto (0,1) com uma
inclinação exatamente igual a 1. Esse número existe realmente e é denotado pela letra e. O número e é o


valor de 1 
n
1
 para n com valores muito grandes e aparece em fórmulas de Matemática Financeira ou
n
em problemas envolvendo crescimentos exponenciais. É conhecido como número (irracional) de Neper.
Representa-se por (e = 2,7182818...). As calculadoras científicas possuem uma tecla que facilita o cálculo.
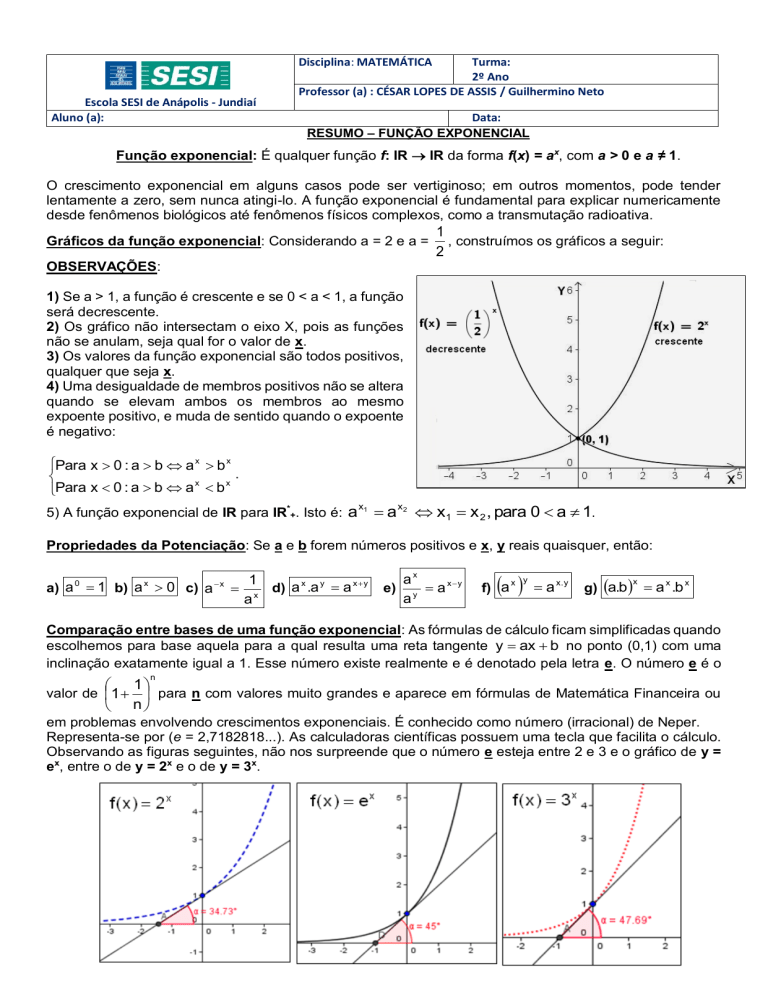
Observando as figuras seguintes, não nos surpreende que o número e esteja entre 2 e 3 e o gráfico de y =
ex, entre o de y = 2x e o de y = 3x.
FUNÇÃO EXPONENCIAL
01.
Em uma região litorânea, a população de
a) Faça uma tabela para representar o valor dessa
certa espécie de alga tem crescido de modo que a
máquina depois de 1,2,3 e 4 anos da data de
área estimada da superfície coberta pelas algas
aquisição.
aumenta 75% a cada ano, em relação à área da
b) Obtenha a lei que relaciona o preço atual (p) em
superfície anterior. Biólogos estimam que,
função do tempo (t) de uso.
atualmente, a área coberta é de aproximadamente
4000 m2. Mantido esse crescimento, qual será a
06.
Admita que, em certo munícipio, a
área da superfície coberta pelas algas daqui:
população cresça à taxa de 15% ao ano.
a) 2 anos
b) 3 anos
c) x anos
Classifique como V ou F a afirmação a seguir e
02.
Em uma experiência sobre deterioração de
alimentos, constatou-se que a população de certo
tipo de bactéria dobrava a cada hora. No instante
em que começaram as observações, havia 50
bactérias na amostra.
a) Faça uma tabela para representar a população
de bactérias nos seguintes instantes (a partir do
início da contagem): 1 hora, 2 horas, 3 horas, 4
hora, 5 horas.
b) Obtenha a lei que relaciona o número de
bactérias (n) em função do tempo (t).
03.
Imagine que a população de uma cidade
cresça à taxa de 5% ao ano. Nessa taxa, já estão
computados os índices de mortalidade,
natalidade, migrações, etc. Admita que a
população atual dessa cidade seja de 10 000
habitantes.
a) Faça uma tabela para representar a população
dessa cidade daqui a um, dois, três, quatro e cinco
anos (contados a partir desta data).
b) Qual é a lei da função que representa o número
de habitantes (y) que essa cidade terá daqui a x
anos.
04.
No dia 1º de janeiro, dois amigos criaram
um canal no “youtube”. No dia seguinte, cada um
dos “fundadores” convidou três novos amigos para
se integrarem ao canal. No dia 3 de janeiro, cada
novo integrante convidou três novos amigos para
se juntarem e assim por diante. Admita que todos
os convidados aceitem a proposta de se integrar à
comunidade e que ninguém receba o convite de
mais de uma pessoa.
a) Quantos membros ingressarão no dia 4? Dia 5?
b) Qual é o total de membros o canal possuirá no
dia 5?
c) Qual é a lei que relaciona o número de membros
(m) que ingressarão no site no dia d.
d) Faça uma estimativa do número de pessoas
que serão convidadas no 31. (Use aproximação
310  6.10 4 )
05.
Uma máquina industrial foi comprada por
R$ 20000,00. Com o tempo, essa máquina se
deprecia a taxa de 20% ao ano de uso.
justifique sua resposta:
“Em cinco anos a população do munícipio já terá
dobrado em relação a seu valor atual.”
07.
Se f(t) = 10.2t é uma função que avalia a
evolução de uma cultura de bactérias, em t horas,
ao cabo de quantas horas teremos f(t) = 5120?
08.
Uma imobiliária acredita que o valor v de
um imóvel no litoral varia segundo a lei
v(t )  60000.(0,9) t , em que t é o número de anos
contados a partir de hoje.
a) Qual é o valor atual desse imóvel?
b) Qual é a desvalorização percentual anual desse
imóvel?
c) Quanto valerá esse imóvel daqui a 2 anos?
d) Daqui a quantos anos o imóvel valerá
R$35429,40? (Dado: 9 5  59049)
09.
Suponha que o número de indivíduos de
uma determinada população seja dado pela
função: F(t)=a.2-b.t , onde a variável t é dada em
anos e a e b são constantes.
a) Encontre as constantes a e b de modo que a
população inicial (t=0) seja igual a 1024 indivíduos
e a população após 10 anos seja a metade da
população inicial.
b) Qual o tempo mínimo para que a população se
reduza a 1/8 da população inicial?
Uma população de bactérias começa com
100 e dobra a cada três horas. Assim, o número
n de bactérias após t horas é dado pela função
10.
n t 
t
 100  2 3 . Nessas condições, pode-se
afirmar que a população será de
bactérias depois de quanto tempo?
51.200
11.
Suponha que o crescimento de uma cultura
t
de bactérias obedece à lei n t   m  2 2 na qual
n representa o número de bactérias no momento
t, medido em horas. Se, fim de 8 horas o número
delas era 3200. Quantas bactérias existiam
inicialmente?