Revisional de Matemática Lidiane 1º Ano

REVISIONAL DE MATEMÁTICA – 1° ANO - PROFESSORA LIDIANE – 2º BIMESTRE/2016
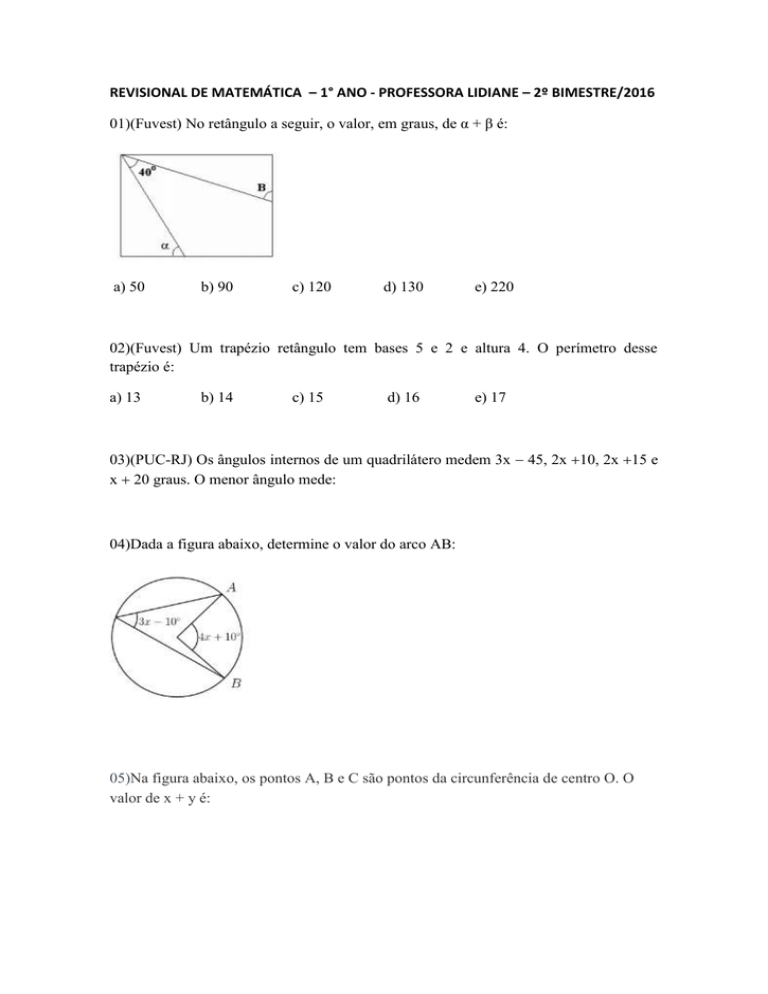
01)(Fuvest) No retângulo a seguir, o valor, em graus, de α + β é:
a) 50
b) 90
c) 120
d) 130
e) 220
02)(Fuvest) Um trapézio retângulo tem bases 5 e 2 e altura 4. O perímetro desse
trapézio é:
a) 13
b) 14
c) 15
d) 16
e) 17
03)(PUC-RJ) Os ângulos internos de um quadrilátero medem 3x  45, 2x 10, 2x 15 e
x  20 graus. O menor ângulo mede:
04)Dada a figura abaixo, determine o valor do arco AB:
05)Na figura abaixo, os pontos A, B e C são pontos da circunferência de centro O. O
valor de x + y é:
06)Determine o valor do ângulo x, conforme a figura abaixo:
07) (Ufjf-pism 1 2016) Na figura a seguir, representa-se um hexágono regular ABCDEF em que cada
lado mede 12 centímetros.
Determine:
a)O valor da medida do perímetro e da área do hexágono regular ABCDEF.
b) O valor das medidas das diagonais CF e CE deste hexágono regular ABCDEF.
c)A razão entre as medidas dos comprimentos dos círculos circunscrito e inscrito, ao hexágono regular
ABCDEF.
08) (Unesp 2016) Uma mesa de passar roupa possui pernas articuladas AB e CD, conforme indica a
figura. Sabe-se que AB  CD  1m, e que M é ponto médio dos segmentos coplanares AB e CD.
ˆ é
Quando a mesa está armada, o tampo fica paralelo ao plano do chão e a medida do ângulo AMC
60.
Considerando-se desprezíveis as medidas dos pés e da espessura do tampo e adotando 3  1,7, a
altura do tampo dessa mesa armada em relação ao plano do chão, em centímetros, está entre
a) 96 e 99.
b) 84 e 87.
c) 80 e 83.
d) 92 e 95.
e) 88 e 91.
09) (G1 - cftmg 2015) Somando-se todos os ângulos internos de três polígonos convexos obtém-se
2160. Sabe-se que o número de lados desses polígonos é n  2, n e n  2. Dentre eles, o que possui
menor número de lados é um
a) triângulo.
b) quadrilátero.
c) pentágono.
d) hexágono.
10) (G1 - utfpr 2015) Os ângulos externos de um polígono regular medem 15 . O número de diagonais
desse polígono é:
a) 56.
b) 24.
c) 252.
d) 128.
e) 168.
TEXTO PARA A PRÓXIMA QUESTÃO:
Considere o texto e o esquema para responder a(s) questão(ões).
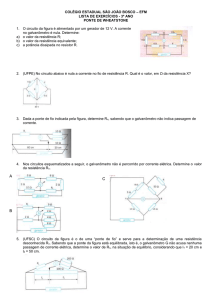
Para se transpor um curso de água ou uma depressão de terreno pode-se construir uma ponte.
Na imagem, vemos uma ponte estaiada, um tipo de ponte suspensa por cabos (estais) fixados em
mastros.
O esquema apresenta parte da estrutura de uma ponte estaiada do tipo denominado harpa, pois os
estais são paralelos entre si. Cada estai tem uma extremidade fixada no mastro e a outra extremidade
no tabuleiro da ponte (onde estão as vias de circulação).
No esquema, considere que:
-as retas AB e BC são perpendiculares entre si;
- os segmentos AC e DE são paralelos entre si e representam estais subsequentes;
- AB  75 m, BC  100 m e AD  6 m; e,
- no mastro dessa ponte, a partir do ponto A em sentido ao ponto B, as extremidades dos estais
estãofixadas e distribuídas a iguais distâncias entre si.
11) (G1 - cps 2015) De acordo com as informações relativas ao esquema, o número máximo de estais
que estão fixados do ponto A ao ponto B e que têm a outra extremidade na semirreta BC é
a) 7.
b) 9.
c) 11.
d) 13.
e) 15.
12) (G1 - cftmg 2014) Considere a figura em que r // s // t .
O valor de x é
a) 3.
b) 4.
c) 5.
d) 6.
13) (Unesp 2014) Em um plano horizontal encontram-se representadas uma circunferência e as cordas
AC e BD. Nas condições apresentadas na figura, determine o valor de x.
14) (G1 - cps 2012) Para melhorar a qualidade do solo, aumentando a produtividade do milho e da soja,
em uma fazenda é feito o rodízio entre essas culturas e a área destinada ao pasto. Com essa finalidade,
a área produtiva da fazenda foi dividida em três partes conforme a figura.
Considere que
– os pontos A, B, C e D estão alinhados;
– os pontos H, G, F e E estão alinhados;
– os segmentos AH, BG, CF e DE são, dois a dois, paralelos entre si;
– AB  500 m, BC  600 m, CD  700 m e HE  1980 m.
Nessas condições, a medida do segmento GF é, em metros,
a) 665.
b) 660.
c) 655.
d) 650.
e) 645.