ˆ 2. . .cosA abc bc = +

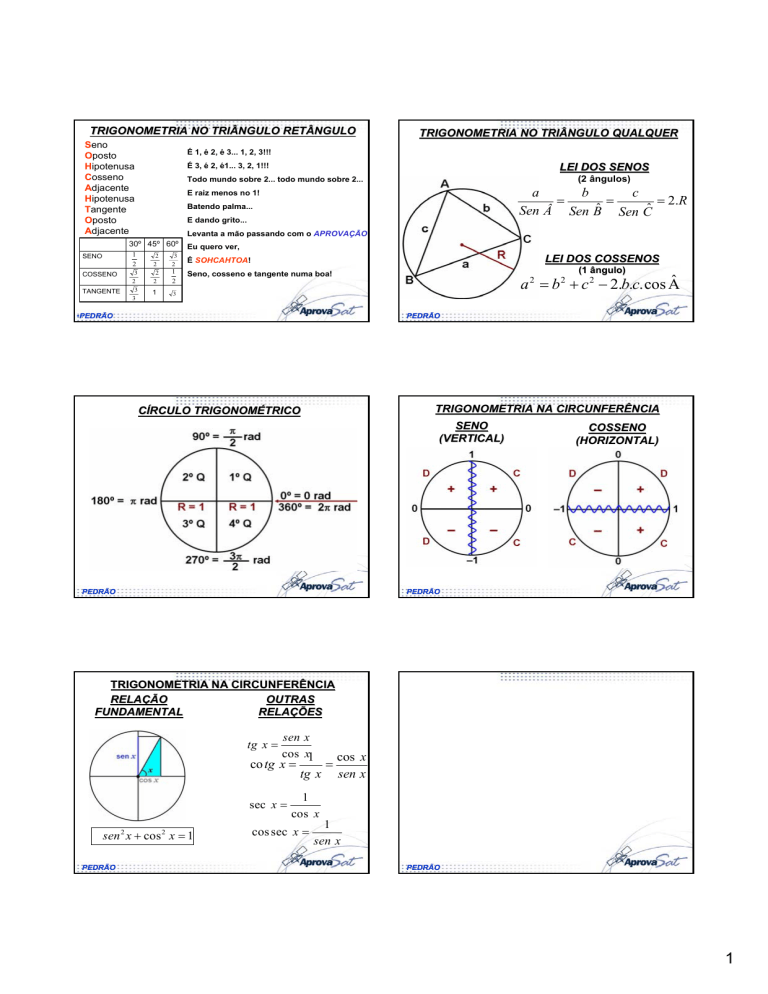
TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
Seno
Oposto
Hipotenusa
Cosseno
Adjacente
Hipotenusa
Tangente
Oposto
Adjacente
É 1, é 2, é 3... 1, 2, 3!!!
É 3, é 2, é1... 3, 2, 1!!!
1
2
COSSENO
3
2
3
3
TANGENTE
LEI DOS SENOS
(2 ângulos)
Todo mundo sobre 2... todo mundo sobre 2...
a
b
c
=
=
= 2.R
ˆ
Sen  Sen B Sen Cˆ
E raiz menos no 1!
Batendo palma...
E dando grito...
Levanta a mão passando com o APROVAÇÃO!
30º 45º 60º
SENO
TRIGONOMETRIA NO TRIÂNGULO QUALQUER
Eu quero ver,
2
2
2
2
3
2
É SOHCAHTOA!
1
2
Seno, cosseno e tangente numa boa!
1
3
LEI DOS COSSENOS
(1 ângulo)
2
ˆ
a = b + c − 2.b.c.cos A
2
•PEDRÃO
2
PEDRÃO
TRIGONOMETRIA NA CIRCUNFERÊNCIA
CÍRCULO TRIGONOMÉTRICO
SENO
(VERTICAL)
PEDRÃO
COSSENO
(HORIZONTAL)
PEDRÃO
TRIGONOMETRIA NA CIRCUNFERÊNCIA
RELAÇÃO
OUTRAS
FUNDAMENTAL
RELAÇÕES
tg x =
sen x
cos x1
co tg x =
sec x =
sen 2 x + cos 2 x = 1
PEDRÃO
tg x
=
cos x
sen x
1
cos x
cos sec x =
1
sen x
PEDRÃO
1
REDUÇÃO AO 1º QUADRANTE
PEDRÃO
Um pequeno avião deveria partir de uma cidade A
rumo a uma cidade B ao norte, distante 60km de
A. Por um problema de orientação, o piloto seguiu
erradamente rumo ao oeste. Ao perceber o erro,
ele corrigiu a rota, fazendo um giro de 120,º à
direita em um ponto C, de modo que o seu trajeto,
juntamente com o trajeto que deveria ter sido
seguido, formaram, aproximadamente, um
triângulo retangular ABC, como mostra a figura.
Com base na figura, a distância em quilômetros
que o avião voou partindo de A até chegar a B é:
PEDRÃO
B
Os ponteiros de um relógio circular medem, do
centro às extremidades, 2 metros, o dos minutos,
e 1metro, o das horas.Determine a distância entre
as extremidades dos ponteiros quando o relógio
marca 4 horas.
120º
C
A
PEDRÃO
2. cos sec x − 3. sec x
3
e sen x = , com x no 2º
5
tgx + cot gx
quadrante, então y é igual a:
Se y =
PEDRÃO
PEDRÃO
Simplificando a expressão
y = sen 17º .cotg17o . cotg 73º . sec 73º,
encontramos:
PEDRÃO
2
O valor numérico da expressão
para x = π é:
⎛ x⎞
cos4x + 2tg⎜ ⎟ − sen2x
⎝ 2⎠
y=
cotgx. cosecx + sec8x
06) A equação 4. sen2x = 1, para 0° ≤ x ≤ 360° , tem conjunto
verdade igual a:
2
PEDRÃO
A solução da equação 2 sen2x + 3senx = 2 para
é:
0 ≤ x ≤ 2π
PEDRÃO
Calculando o valor numérico da expressão abaixo,
obtemos:
(sen30 o − cos120 o ).(cosec150 o − cotg330 o )
(sec300 o + tg60 o . cotg225 o )
PEDRÃO
PEDRÃO
PEDRÃO
3