R → R uma função

Fundamentos de Equações Diferenciais
Segunda Lista de Exercícios - 02/2016
Série de Fourier
1. Dada f : R → R uma função periódica de período T , integrável em qualquer intervalo, mostre que
ˆ a+T
ˆ T
f (x)dx =
f (x)dx,
a
0
no qual a é um número real qualquer fixado.
2. A soma de duas funções periódicas de períodos diferentes podem, ou não, ser periódicas. Exemplifique ambos
os casos.
3. Mostre que, se f1 : R → R é periódica de período T1 e f2 : R → R é periódica de período T2 , e se existem
m, n ∈ Z tais que mT1 = nT2 , então f1 + f2 é periódica de período mT1 .
4. Mostre que sin ax + sin bx é periódica se, e somente se, a/b ∈ Q.
5. Mostre que se f : R → R for uma função par, e f (x) 6= 0, então 1/f é uma função par. Mesmo problema para
funções ímpares.
6. Se f : R → R for uma função par diferenciável então f 0 será ímpar. Mostre também que, se f : R → R é
ímpar e diferenciável, então f 0 é par.
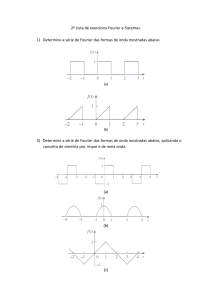
7. Determine os coeficientes de Fourier para as funções:
(a) f (x) = 2 cos(πx) + e sin(3πx)
(b) f (x) = x definida no intervalo [−e, e] periódica de período 2e.
(c) f (x) = ex + e−x definida no intervalo [−1, 1] periódica de período 2.
(d) f (x) = cos αx, α ∈ R6=0 .
8. Determine as séries de Fourier das seguintes funções apenas utilizando relações trigonométricas.
(a) f (x) = sin2 (x)
(b) f (x) = cos5 (x)
9. Calcule a série de Fourier da onda senoidal retificada, isto é,
(
sin x se sin(x) ≥ 0
f (x) =
0
caso contrário.
10. Use a série de Fourier da função
f (x) = cos αx, α ∈ R∗
para mostrar que
1
cot απ =
π
∞
1 X 2α
−
α n=1 n2 − α2
quando α não é inteiro.
1
!
,
11. Quais são as relações entre os coeficientes de Fourier da função f (x), periódica de período 2L, e da função
g(x) = f (x + α), em que α é uma constante?
12. Use a forma complexa para obter as séries de Fourier das seguintes funções.
(a) f (x) = cos(αx) e g(x) = sin(αx) definidas em −π ≤ x ≤ π, periódicas de período 2π e α um número não
inteiro.
(b) f (x) = eαx definida em −π ≤ x ≤ π, periódica de período 2π e α um número não inteiro.
13. Determine as funções cujas séries de Fourier estão abaixo indicadas.
∞
∞
X
X
cos nx
sin nx
e
.
n!
n!
n=1
n=1
14. Mostre que
1
2
coth π = +
π π
em que coth x =
cosh x
sinh x
=
ex +e−x
ex −e−x
1
1
1
+
+
+ ···
1 + 12
1 + 22
1 + 32
,
é a função cotangente hiperbólica.
Equação do Calor
1. Encontre a solução em série do problema de valor inicial e fronteira para a equação do calor ut = uxx para
0 < x < 1, com condição inicial u(x, 0) = f (x) quando uma extremidade da barra é mantida a 0◦ e a outra é
isolada. Discuta o comportamento assintótico da solução quando t → ∞.
2. Uma barra de metal de comprimento ` = 1 e difusividade térmica γ = 1 é totalmente isolada, incluindo suas
extremidades. Suponha que a distribuição inicial de temperatura seja
(
x,
0 ≤ x ≤ 21
u(x, 0) =
.
1 − x, 12 ≤ x ≤ 1
(a) Use a série de Fourier para escrever a distribuição de temperatura no tempo t > 0.
(b) Qual é a distribuição da temperatura de equilíbrio na barra, isto é, para t → ∞?
3. Resolva o problema de valor inicial e de fronteira
ut
ux (x, t)
u(x, 0)
= c2 uxx
= ux (L, t) + αu(L, t) = 0, t > 0
= f (x), 0 < x < L.
4. Resolva o problema de valor inicial e de fronteira
ut
ux (x, 0)
u(x, 0)
= c2 uxx + g(x)
= ux (L, t) = 0, t > 0
=
f (x), 0 < x < L.
Equação da Onda
1. Resolva o problema de valor inicial e de fronteira
utt
=
u(x, t)
= α,
u(x, 0)
= f (x),
c2 uxx
u(L, t) = β, t > 0
ut (x, 0) = g(x), 0 < x < L,
em que α, β são constantes. Para tal realize uma mudança de variáveis adequada de forma que o problema
transformado possua as condições de fronteira homogêneas.
2
2. Use o método da separação de variáveis para determinar a solução do problema de valor inicial e de fronteira
relacionado a equação da onda:
∂u
∂2u
∂2u
+ 2β
, (x, t) ∈ [0, π] × R+ , 0 < β < 1
=
2
∂t
∂t
∂x2
com u(0, t) = u(π, t) = 0, para t > 0, u(x, 0) = x(π − x) e ut (x, 0) = 0, 0 ≤ x ≤ π.
3. Mostre que a solução para o problema da onda utt = c2 uxx , com condições de contorno u(0, t) = u(L, t) = 0
e com u(x, 0) = 0 e ut (x, 0) = g(x), pode ser escrita, em termos da extensão periódica ímpar de g(x), g ∗ (x),
na seguinte forma integral:
ˆ x+ct
1
u(x, t) =
g ∗ (s)ds
2c x−ct
4. Considere uma corda elástica, de comprimento L, fixada nas suas duas extermiades. Uma das extremidades é
fixada em uma altura de referência (por exemplo, u(x, 0) = 0). A outra, por um erro de montagem, é fixada
em uma pequena altura ε. Resolva este problema e compare a sua solução com o caso em que a corda é
montada corretamente. O som produzido pela corda montada com o desvio de altura será diferente daquele
esperando?
Equação de Laplace
1. Determine relações entre as constantes a, b, c e d de modo que u(x, y) = ax3 + 3bx2 y + 3cxy 2 + dy 3 seja
harmônica.
2. Mostre que a equação de Laplace em coordenadas polares é
1 ∂2v
∂ 2 v 1 ∂v
+
+ 2 2 = 0.
2
∂r
r ∂r
r ∂θ
3. Determine a função u(x, y) que seja harmônica na região x2 + y 2 < 1 e tal que quando x2 + y 2 = 1, tenhamos
y
u(x, y) = 1 + p
.
x2 + y 2
4. Mostre que a função
v(r, θ) =
∞
X
rn (an cos nθ + bn sin nθ)
n=0
definida para r < ρ e 0 ≤ θ ≤ 2π, pode ser escrita como
ˆ 2π
1
ρ2 − r 2
f (α)dα.
v(r, θ) =
2π 0 ρ2 + r2 − 2ρr cos(θ − α)
Essa fórmula é conhecida como fórmula de Poisson.
3
Resumo do Conteúdo
• A série de Fourier de uma função f : R → R periódica de período 2L é dada por
f (x) ∼
∞ a0 X
kπ
kπ
+
x + bk sin
x ,
ak cos
2
L
L
k=1
e seus coeficientes por
ak
=
bk
=
ˆ
L
kπ
x dx, k ≥ 0
L
−L
ˆ L
1
kπ
f (x) sin
x dx, k ≥ 1.
L −L
L
1
L
f (x) cos
• A forma complexa da série de Fourier de uma função f : R → R periódica de período 2L é dada por
∞
X
f (x) ∼
cn eikn x ,
n=−∞
com kn = nπx/L e
1
cn =
2L
ˆ
L
f (x)e−ikn x dx, n ∈ Z.
−L
• Paridade: Uma função f : R → R é dita par se, dado x ∈ R, f (x) = f (−x). Além disso, dada uma função
f : R → R tal que f (x) = −f (−x) para todo x ∈ R dizemos que ela é ímpar .
– Para f (x) par os coeficientes de Fourier são dados por
ak
bk
ˆ
2 L
kπ
=
x dx, k ≥ 0
f (x) cos
L 0
L
= 0, k ≥ 1.
– Para f (x) ímpar os coeficientes de Fourier são dados por
ak
=
bk
=
0, k ≥ 0
ˆ
2 L
kπ
f (x) sin
x dx, k ≥ 1.
L −L
L
• Teorema de Fourier
Seja f : R → R uma função seccionalmente diferenciável de período 2L. Então, a série de Fourier de f
converge em cada ponto x para
1
lim+ f (y) + lim− f (y) ,
2 y→x
y→x
isto é,
1
2
∞ X
1
nπx
nπx lim+ f (y) + lim− f (y) = a0 +
an cos
+ bn sin
.
2
L
L
y→x
y→x
n=1
4