universidade regional do cariri – urca pró-reitoria de

UNIVERSIDADE REGIONAL DO CARIRI – URCA
PRÓ-REITORIA DE ENSINO E GRADUAÇÃO – PROGAD
DEPARTAMENTO DE MATEMÁTICA
UNIDADE DESCENTRALIZADA DE CAMPOS SALES – CAMPI CARIRI OESTE
DISCPLINA: Geometria Plana e Espacial
SEMESTRE: II
PROFESSOR: Cicefran Souza de Carvalho
Aluno: ____________________________________________________________________
ATIVIDADE GEOMETRIA PLANA – AV2
1. Mostre que se um ângulo e seu suplemento têm a mesma medida, então ele é um
ângulo reto.
2. Um ângulo é chamado agudo se mede menos de 90°, e chamado obtuso se mede mais
de 90º. Mostre que o suplemento de um ângulo agudo é sempre obtuso.
3. Use um transferidor e desenhe ângulos de 45º, 60º, 90º, 142º, 15,5° e 33º.
4. Dois ângulos são ditos complementares se sua soma é um ângulo reto. Dois ângulos
são complementares e o suplemento de um deles mede tanto quanto o suplemento do
segundo mais 30º. Quanto medem os dois ângulos?
5. Uma poligonal é uma figura formada por uma sequência de pontos 𝐴1 , 𝐴2 … , 𝐴𝑛 e
pelos segmentos 𝐴1 𝐴2 , 𝐴2 𝐴3 , 𝐴3 𝐴4 , … , 𝐴𝑛−1 𝐴𝑛 . Os pontos são os vértices da poligonal
e os segmentos são os seus lados. Desenhe a poligonal A B C D sabendo que 𝐴𝐵 =
𝐵𝐶 = 𝐶𝐷 = 2 𝑐𝑚, 𝐴 𝐵 𝐶 = 120° 𝑒 𝐵 𝐶 𝐷 = 100°
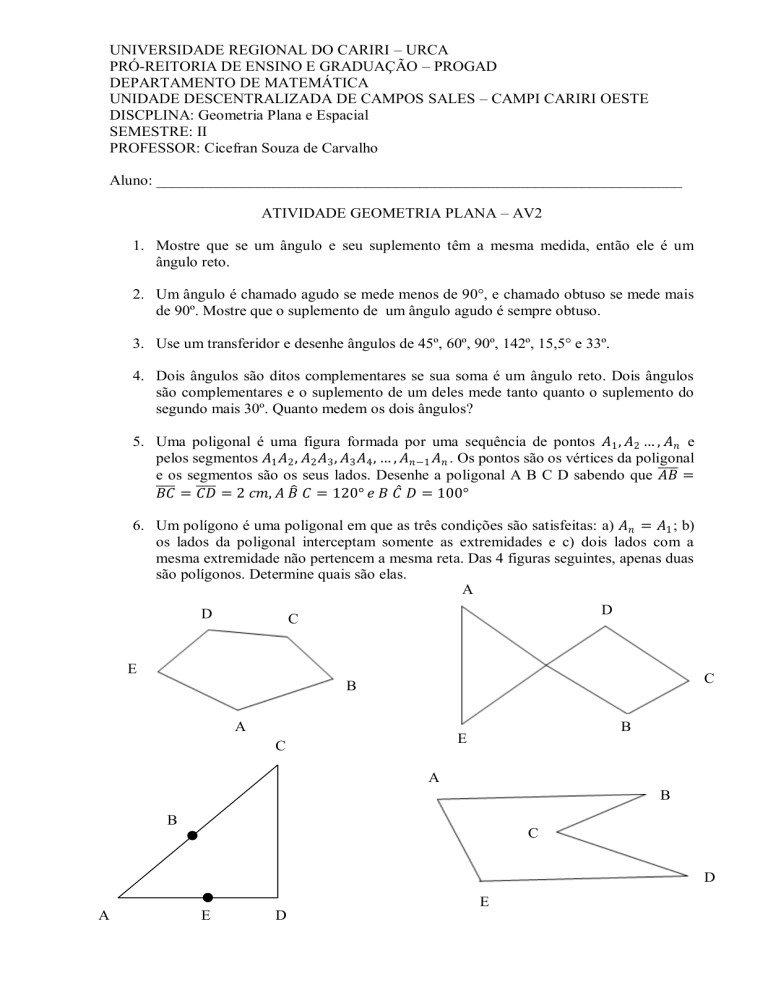
6. Um polígono é uma poligonal em que as três condições são satisfeitas: a) 𝐴𝑛 = 𝐴1 ; b)
os lados da poligonal interceptam somente as extremidades e c) dois lados com a
mesma extremidade não pertencem a mesma reta. Das 4 figuras seguintes, apenas duas
são polígonos. Determine quais são elas.
A
D
D
C
E
C
B
A
B
E
C
A
B
B
C
D
E
A
E
D
UNIVERSIDADE REGIONAL DO CARIRI – URCA
PRÓ-REITORIA DE ENSINO E GRADUAÇÃO – PROGAD
DEPARTAMENTO DE MATEMÁTICA
UNIDADE DESCENTRALIZADA DE CAMPOS SALES – CAMPI CARIRI OESTE
DISCPLINA: Geometria Plana e Espacial
SEMESTRE: II
PROFESSOR: Cicefran Souza de Carvalho
7. Desenhe um polígono de 4 lados A, B, C, D, tal que 𝐴𝐵 = 𝐵𝐶 = 𝐶𝐷=𝐷𝐴 = 2 𝑐𝑚,
com 𝐴 𝐵 𝐶 = 𝐴 𝐷 𝐶 = 100° e com 𝐵 𝐶 𝐷 = 𝐵 𝐴 𝐷 = 80°.
8. Construa um triângulo A B C sabendo que 𝐴𝐵 = 7,5 𝑐𝑚, 𝐵𝐶 = 8,2 𝑐𝑚 𝑒 𝐴 𝐵 𝐶 =
80°. Meça o comprimento de BC e os outros ângulos do triângulo.
9. Na figura abaixo os ângulos 𝛼 𝑒 𝛽 são iguais. Mostre que AC = BC.
A
𝛼
C
𝛽
B
10. Na figura ao lado, AC = AD e AB é a bissetriz do ângulo C Â D. Prove que os
triângulos ACB e ADB são congruentes.
C
A
B
D
UNIVERSIDADE REGIONAL DO CARIRI – URCA
PRÓ-REITORIA DE ENSINO E GRADUAÇÃO – PROGAD
DEPARTAMENTO DE MATEMÁTICA
UNIDADE DESCENTRALIZADA DE CAMPOS SALES – CAMPI CARIRI OESTE
DISCPLINA: Geometria Plana e Espacial
SEMESTRE: II
PROFESSOR: Cicefran Souza de Carvalho
11. A figura ao lado é formada pelos segmentos AC, AE, CF e EB. Determine os ângulos
que são:
a) Menores que o ângulo 7.
b) Maiores que o ângulo 5 e
c) Menores que o ângulo 4
12. De acordo com a figura ao lado responda as seguintes perguntas:
a) Os triângulo ABCe DCB são congruentes?
b) Qual o lado do triângulo ABC que é mais longo?
c) Qual o lado do triêngulo DCB que é mais curto?
13. Determine o valor de x e y, sendo r // s.
70°
4x
y
r
x
y
x+15
3x
14. Num triângulo ABC, 𝐴𝐵 = 5, 𝐵𝐶 = 12 𝑒 𝐶𝐴 = 13. Qual a medida do ângulo 𝐵?
15. Num triângulo DEF, 𝐷𝐸 = 𝐸𝐹 = 6 𝑒 𝐹𝐷 = 6 2. Quanto medem os ângulos de
triângulo?
UNIVERSIDADE REGIONAL DO CARIRI – URCA
PRÓ-REITORIA DE ENSINO E GRADUAÇÃO – PROGAD
DEPARTAMENTO DE MATEMÁTICA
UNIDADE DESCENTRALIZADA DE CAMPOS SALES – CAMPI CARIRI OESTE
DISCPLINA: Geometria Plana e Espacial
SEMESTRE: II
PROFESSOR: Cicefran Souza de Carvalho
16. Se o triângulo ABC é isósceles de base 𝐴𝐶 . Determine x. (dados  = x + 30º e
𝐶 = 2𝑥 − 20°
17. Por que ALL ou LLA não é um caso de congruência de triângulos?
18. Na figura abaixo, os triângulos ABC e CDA são congruentes. Calcule x e y.
27°
120°
2y
3y
19. Com segmentos de 8 cm, 5cm e 18 cm, pode-se construir um triângulo? Justifique.
20. Se dois lados de um triângulo isósceles medem 38 cm e 14 cm, qual poderá ser a
medida do terceiro lado?
21. Calcule a soma dos ângulos internos de icoságono.
22. Determine o polígono que tem 9 diagonais distintas.