Mat Aplicada Apostila aula 1

MATEMÁTICA APLICADA
Profª Sandra Regina
AULA 1
RELAÇÕES
- PRODUTO CARTESIANO
Sejam os conjuntos A= { 0, 1, 2} E B= { 2, 4}.
Vamos formar conjunto dos pares ordenados onde o primeiro elemento do par
pertence ao conjunto A e o segundo pertence ao conjunto B;
{ (0, 2), (0, 4), (1, 2), ( 1,40, (2,02), (2,4)}
O conjunto de pares assim formados denomina-se produto cartesiano de A por
B e indica-se AXB ( lê-se: A cartesiano B).
Então:
Dados dois conjuntos não vazios A e B, denomina-se produto cartesiano de
A por B o conjunto formado pelos pares ordenados nos quais o primeiro elemento
pertence a A e o segundo elemento pertence a B.
AXB = { x, y)| x  A e y  B}
Observações:
1º) Se A = Ø ou B = Ø, por definição, AXB = Ø, isto é, AX Ø = Ø ou ØXB =
Ø
2º) Se A = B, podemos escrever o produto cartesiano AXA como A², isto é
AXA = A².
3º) sendo A e B não vazios, temos AXB ≠ BXA.
4º) Sendo n(A) = 3 o conjunto de elementos do conjunto A, n(B) + 2 o número
de elementos do conjunto B e n (AXB) = 6 o número de elementos de AXB, temos:
6 = 2. 3  n(AXB) = n(A). n(B)
- RELAÇÃO BINÁRIA
Um conjunto de pares ordenados de números reais chama-se uma relação binária. O
conjunto dos primeiros elementos de uma relação binária chama-se o domínio da
relação; o conjunto dos segundos elementos denomina-se a imagem da relação. Para um
dado conjunto {(x,y)}, x e y são as variáveis. O conjunto dos valores da variável x é o
domínio e x é usualmente chamada de variável independente; o conjunto dos valores da
variável y é a imagem e y é usualmente chamada de variável dependente. Quando o
número de variáveis é claro no contexto, uma relação binária será chamada,
simplesmente, de relação.
Dados dois conjuntos A e B, dá-se o nome de relação R de A em B a qualquer
subconjunto de A X B.
EXEMPLO
S 1 = {(1, 2), (2, 8), ( 2, 3)} é uma relação binária cujo domínio é {1, 2} e cuja imagem é
{2, 3, 8}.
S 2 = { ( x, y) : x e y são números reais, x  y} é uma relação binária. (2, 2), ( 3, 4),
(5,5), (8, 20) são alguns elementos dessa relação. Observe que ( 2, 1), ( 3, 2) e ( 25, 20),
por exemplo, não são elementos de S 2 .
EXERCÍCIOS
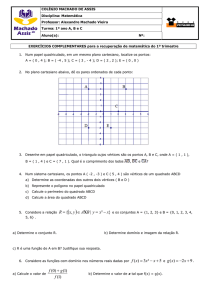
1) Dados A = { -1, 0, 1 }, B = { 0,2 } e C {1, 2}, determine:
a) AXB
b) AXC
c) BXA d) A² e) B²
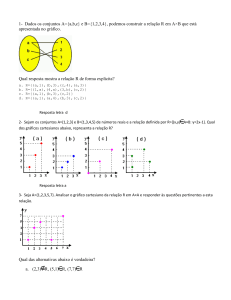
2) Dados A = { -2, -1, 0 , 1} e B = { -1, 0, 1, 2, 3, 4 }, determine as relações de A em B.
a) R 1 = { (x,y)  A X B | y = x + 1}
b) R 2 = { (x,y)  A X B | y = x² }
c ) R 3 = { (x,y)  A X B | y = x – 2}
d ) R 4 = { (x,y)  A X B | x + y = 5}
e) Calcule o domínio e a imagem das relações acima.