matemática

Simulado IME-ITA
MATEMÁTICA
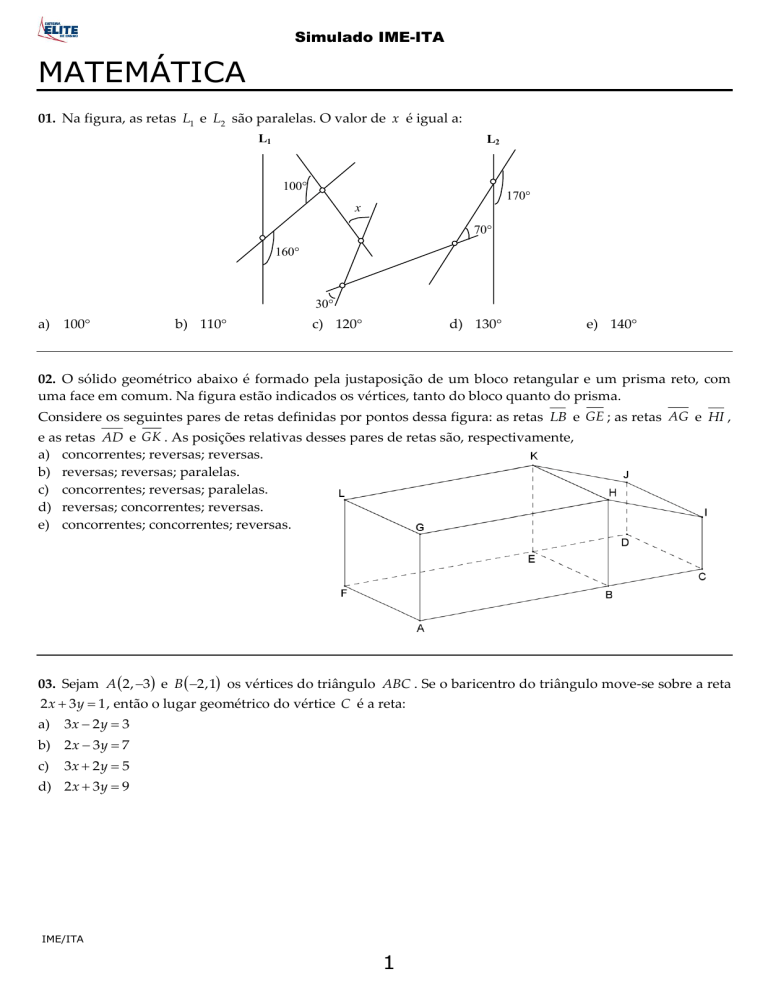
01. Na figura, as retas L1 e L2 são paralelas. O valor de x é igual a:
L1
L2
100
170
x
70
160
30
a) 100
b) 110
c) 120
d) 130
e) 140
02. O sólido geométrico abaixo é formado pela justaposição de um bloco retangular e um prisma reto, com
uma face em comum. Na figura estão indicados os vértices, tanto do bloco quanto do prisma.
Considere os seguintes pares de retas definidas por pontos dessa figura: as retas LB e GE ; as retas AG e HI ,
e as retas AD e GK . As posições relativas desses pares de retas são, respectivamente,
a) concorrentes; reversas; reversas.
b) reversas; reversas; paralelas.
c) concorrentes; reversas; paralelas.
d) reversas; concorrentes; reversas.
e) concorrentes; concorrentes; reversas.
03. Sejam A 2, 3 e B  2,1 os vértices do triângulo ABC . Se o baricentro do triângulo move-se sobre a reta
2 x  3 y  1 , então o lugar geométrico do vértice C é a reta:
a)
3x  2 y  3
b) 2 x  3 y  7
c)
3x  2 y  5
d) 2x  3y  9
IME/ITA
1
1
Simulado IME-ITA
04. Na figura seguinte ABCD é um quadrado de lado 1 e BCE é um triângulo equilátero. O valor de tan

2
é
igual a:
a) 1 
3
2
b) 2 
6
2
c) 1 
3
3
d) 1 
2
5
1
, então sen x  sec x vale:
3
10
15 10
c) 
d) 
5
32
e) 1 
3
5
05. Se x é um arco do terceiro quadrante e tg x 
a)
10
3

b) 
13 10
30
e) 
3 10
5
06. Em uma progressão aritmética, a soma Sn de seus n primeiros termos é dada pela expressão
Sn  5n2  12n , com n 
a)
2
*
. A razão dessa progressão é
b) 4
c) 8
d) 10
e) 12
 f (3)  2
07. Seja f uma função definida para todo real, satisfazendo as seguintes condições: 
.
 f ( x  3)  f ( x)  f (3)
Então f  3  f 0 vale:
a) –6
b) 1
c)
1
2
d)
3
2
08. Um curso oferece as disciplinas A , B , C e D . Foram feitas as matrículas dos alunos da seguinte forma:




6
5
5
4
alunos se matricularam na disciplina
alunos se matricularam na disciplina
alunos se matricularam na disciplina
alunos se matricularam na disciplina
A;
B;
C;e
D.
Sabe-se que cada aluno se matriculou em, no mínimo, 3 disciplinas. Determine a quantidade mínima de
alunos que se matricularam nas 4 disciplinas.
a) 0
b) 1
c) 2
d) 3
e) 4
IME/ITA
2
1
Simulado IME-ITA

1
09. Seja x um número real ou complexo para o qual  x    1 . O valor de

x
a) 1
b) 2
c) 3
d) 4
 6 1
 x  6  é:
x
e) 5
10. Qual das alternativas abaixo apresenta um dos fatores obtidos na fatoração de a4  2a3b  3a2 b2  4ab3  b4 ?
a) a2  ab  b2
b) a2  ab  b2
c) a2  b2
d) a2  3ab  b2
e) a2  3ab  b2
11. Seja n o número de lados de um polígono convexo. Se a soma de n  1 ângulos (internos) do polígono é
2004 , determine o número n de lados do polígono.
12. Encontre o valor mínimo da função f  x , y  
13. Seja
S  n
a
soma
dos
primeiros
S n  3  3  S n  2   3  S n  1  S n  0 .
n
 x  12   y  22  x  22   y  32 , onde x, y 
termos
de
uma
progressão
aritmética.
.
Prove
que
14. Sejam a e b constantes reais positivas. Se a equação cos 3 x   a  1 cos 2 x   a  b cos x  b  0 possui duas
raízes reais distintas no intervalo [0 , /2], prove que 0 < b < a + 1.
15.
a) Sejam x , y e z números reais positivos. Prove que:
x yz 3
 x  y  z . Em que condições se verifica a
3
igualdade?
b) Considere um paralelepípedo de lados a , b e c , e área total S0 . Determine o volume máximo desse
paralelepípedo em função de S0 . Qual a relação entre a , b e c para que o volume seja máximo?
Demonstre seu resultado.
IME/ITA
3
1