a) 5 3 5 + c) 20 4 5 + µ

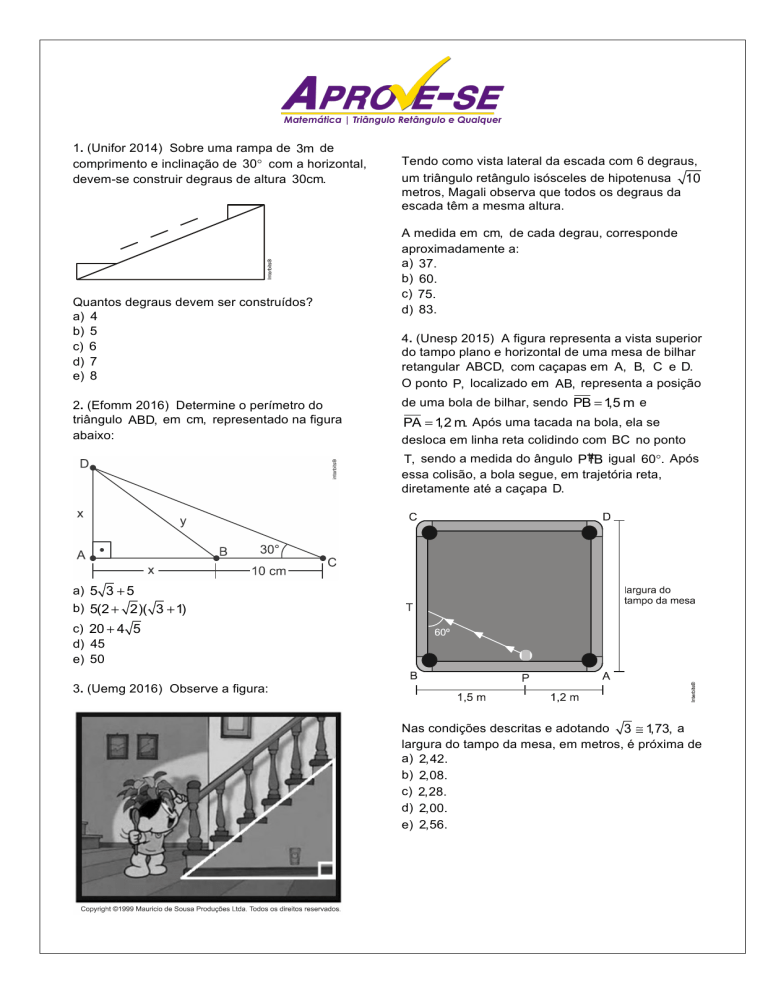
1. (Unifor 2014) Sobre uma rampa de 3m de
comprimento e inclinação de 30° com a horizontal,
devem-se construir degraus de altura 30cm.
Quantos degraus devem ser construídos?
a) 4
b) 5
c) 6
d) 7
e) 8
2. (Efomm 2016) Determine o perímetro do
triângulo ABD, em cm, representado na figura
abaixo:
Tendo como vista lateral da escada com 6 degraus,
um triângulo retângulo isósceles de hipotenusa 10
metros, Magali observa que todos os degraus da
escada têm a mesma altura.
A medida em cm, de cada degrau, corresponde
aproximadamente a:
a) 37.
b) 60.
c) 75.
d) 83.
4. (Unesp 2015) A figura representa a vista superior
do tampo plano e horizontal de uma mesa de bilhar
retangular ABCD, com caçapas em A, B, C e D.
O ponto P, localizado em AB, representa a posição
de uma bola de bilhar, sendo PB = 1,5 m e
PA = 1,2 m. Após uma tacada na bola, ela se
desloca em linha reta colidindo com BC no ponto
µ igual 60°. Após
T, sendo a medida do ângulo PTB
essa colisão, a bola segue, em trajetória reta,
diretamente até a caçapa D.
a) 5 3 + 5
b) 5(2 + 2)( 3 + 1)
c) 20 + 4 5
d) 45
e) 50
3. (Uemg 2016) Observe a figura:
Nas condições descritas e adotando 3 ≅ 1,73, a
largura do tampo da mesa, em metros, é próxima de
a) 2,42.
b) 2,08.
c) 2,28.
d) 2,00.
e) 2,56.
5. A Figura 1 apresenta a imagem de um poste que
pode ser visto nas ruas de algumas cidades
brasileiras.
Assim, a medida do segmento DC vale
a) 10 3.
b) 6 3.
15
.
2
13
d)
.
2
c)
A seguir temos uma representação de um desses
postes (Figura 2), que pode ser dividido em 3
partes: uma haste AB, vertical e fixada no chão
plano (horizontal), medindo 3 metros; uma haste
AE medindo 1 metro, tal que BÂE = 120°; e uma
haste ED, paralela ao chão plano (horizontal).
7. (Puccamp 2016) A figura mostra o ângulo de
visão que um mesmo observador tem de uma
estrutura de caixa d’água em dois pontos diferentes.
Sabe-se que a altura dos olhos, em relação ao piso
plano sobre o qual a estrutura está apoiada
perpendicularmente, é exatamente a metade da
altura da estrutura da caixa d’água, e que a
distância entre os dois pontos de observação é de
2 metros.
Dados:
sen
Uma lâmpada será instalada no ponto D. A altura,
em relação ao chão plano, em que esta lâmpada
será instalada, em metros, é
a) 3,2.
b) 3,5.
c) 3,6.
d) 4,0.
ˆ e os
6. O triângulo ABC é retângulo em ABC
segmentos BD e AC são perpendiculares.
30°
1
2
cos
tan
3
2
3
3
45°
60°
2
2
2
2
3
2
1
2
1
3
A partir dessas informações, é possível determinar
que a altura da estrutura da caixa d’água, em
metros, é igual a
a) 3 3 − 2.
3 +2
.
3
c) 2 3 + 2.
d) 3 + 2.
e) 3 + 1.
b)
8. (Ufrgs 2014) Na figura abaixo, o retângulo ABCD
tem lados que medem 6 e 9.
Se a área do paralelogramo sombreado é 6, o
cosseno de α é
3
a) .
5
2
b) .
3
3
c) .
4
4
d) .
5
8
e) .
9
9. Uma formiga sai do ponto A e segue por uma
trilha, representada pela linha contínua, até chegar
ao ponto B, como mostra a figura.
Sabendo que cada batente tem 20 cm de altura e 30
cm de comprimento (profundidade), a tangente do
ˆ mede:
ângulo CAD
9
a)
10
14
b)
15
29
c)
30
d) 1
11. (Ufsm 2013) A caminhada é uma das atividades
físicas que, quando realizada com frequência, tornase eficaz na prevenção de doenças crônicas e na
melhora da qualidade de vida.
Para a prática de uma caminhada, uma pessoa sai
do ponto A, passa pelos pontos B e C e retorna ao
ponto A, conforme trajeto indicado na figura.
A distância, em metros, percorrida pela formiga é
a) 1 + 2 3.
b) 3 + 3 3.
c) 5 + 2 3.
d) 7 + 3 3.
10. (Ufrn 2013) A escadaria a seguir tem oito
batentes no primeiro lance e seis, no segundo lance
de escada.
Quantos quilômetros ela terá caminhado, se
percorrer todo o trajeto?
a) 2,29.
b) 2,33.
c) 3,16.
d) 3,50.
e) 4,80.
12. (Ufjf 2012) Uma praça circular de raio R foi
construída a partir da planta a seguir:
sob influência do meio urbano é dada pela distância
do ponto A ao ponto C. Essa distância, em km, é
8 6
3
b) 4 6
a)
c) 8 2 + 3
d) 8( 2 + 3)
e)
Os segmentos AB, BC e CA simbolizam ciclovias
construídas no interior da praça, sendo que
AB = 80 m. De acordo com a planta e as
informações dadas, é CORRETO afirmar que a
medida de R é igual a:
a)
b)
c)
d)
e)
160 3
m
3
80 3
m
3
16 3
m
3
8 3
m
3
3
m
3
13. (Ufsm 2011) A figura a seguir apresenta o delta
do rio Jacuí, situado na região metropolitana de
Porto Alegre. Nele se encontra o parque estadual
Delta do Jacuí, importante parque de preservação
ambiental. Sua proximidade com a região
metropolitana torna-o suscetível aos impactos
ambientais causados pela atividade humana.
A distância do ponto B ao ponto C é de 8 km, o
ângulo  mede 45° e o ângulo C mede 75°. Uma
maneira de estimar quanto do Delta do Jacuí está
2 6
3
14. (Uftm 2012) Na figura estão posicionadas as
cidades vizinhas A, B e C, que são ligadas por
estradas em linha reta. Sabe-se que, seguindo por
essas estradas, a distância entre A e C é de 24 km,
e entre A e B é de 36 km.
Nesse caso, pode-se concluir que a distância, em
km, entre B e C é igual a
a) 8 17.
b) 12 19.
c) 12 23.
d) 20 15.
e) 20 13.
15. (Unesp 2011) Uma pessoa se encontra no
ponto A de uma planície, às margens de um rio e
vê, do outro lado do rio, o topo do mastro de uma
bandeira, ponto B. Com o objetivo de determinar a
altura h do mastro, ela anda, em linha reta, 50 m
para a direita do ponto em que se encontrava e
marca o ponto C. Sendo D o pé do mastro, avalia
que os ângulos BÂC e
valem 30°, e o
vale
105°, como mostra a figura:
a) 12,5.
b) 12,5 2 .
c) 25,0.
d) 25,0 2 .
e) 35,0.
16. (Ufpb 2010) A prefeitura de certa cidade vai
construir, sobre um rio que corta essa cidade, uma
ponte que deve ser reta e ligar dois pontos, A e B,
localizados nas margens opostas do rio. Para medir
a distância entre esses pontos, um topógrafo
localizou um terceiro ponto, C, distante 200m do
ponto A e na mesma margem do rio onde se
encontra o ponto A. Usando um teodolito
(instrumento de precisão para medir ângulos
horizontais e ângulos verticais, muito empregado
em trabalhos topográficos), o topógrafo observou
que os ângulos B Ĉ A e C Â B mediam,
respectivamente, 30º e 105º, conforme ilustrado na
figura a seguir.
a) 10 km.
b) 14 km.
c) 15 km.
d) 17 km.
e) 22 km.
19. (Fgv 2013) Na figura, ABCDEF é um hexágono
regular de lado 1 dm, e Q é o centro da
circunferência inscrita a ele.
O perímetro do polígono AQCEF, em dm, é igual a
a) 4 + 2
b) 4 + 3
c) 6
d) 4 + 5
e) 2(2 + 2)
Com base nessas informações, é correto afirmar
que a distância, em metros, do ponto A ao ponto
B é de:
a) 200 2
b) 180 2
c) 150 2
d) 100 2
e) 50 2
17. A base de um triângulo isósceles mede 3 3 cm
e o ângulo oposto à base mede 120°. A medida dos
lados congruentes desse triângulo, em centímetros,
é
a) 3.
b) 2.
c) 3.
d) 1 + 3.
e) 2 − 3.
18. (Ufpr 2014) Dois navios deixam um porto ao
mesmo tempo. O primeiro viaja a uma velocidade
de 16 km/h em um curso de 45° em relação ao
norte, no sentido horário. O segundo viaja a uma
velocidade 6 km/h em um curso de 105° em relação
ao norte, também no sentido horário. Após uma
hora de viagem, a que distância se encontrarão
separados os navios, supondo que eles tenham
mantido o mesmo curso e velocidade desde que
deixaram o porto?
20. Uma rampa faz um ângulo de 30° com o plano
horizontal. Uma pessoa que subiu 20 metros dessa
rampa se encontra a altura de ___ do solo.
a) 6 metros.
b) 7 metros.
c) 8 metros.
d) 9 metros.
e) 10 metros.
Gabarito:
Resposta da questão 1:
[B]
Resposta da questão 2:
[B]
Resposta da questão 3:
[A]
Resposta da questão 4:
[A]
Resposta da questão 5:
[B]
Resposta da questão 6:
[C]
Resposta da questão 7:
[C]
Resposta da questão 8:
[D]
Resposta da questão 9:
[D]
Resposta da questão 10:
[B]
Resposta da questão 11:
[D]
Resposta da questão 12:
[B]
Resposta da questão 13:
[B]
Resposta da questão 14:
[B]
Resposta da questão 15:
[B]
Resposta da questão 16:
[D]
Resposta da questão 17:
[A]
Resposta da questão 18:
[B]
Resposta da questão 19:
[B]
Resposta da questão 20:
[E]