Problemas Resolvidos de Física

PROBLEMAS RESOLVIDOS DE FÍSICA
Prof. Anderson Coser Gaudio
Departamento de Física – Centro de Ciências Exatas – Universidade Federal do Espírito Santo
http://www.cce.ufes.br/anderson
[email protected]
Última atualização: 28/11/2006 14:49 H
19 - Potencial Elétrico
Fundamentos de Física 2
Halliday, Resnick, Walker
4ª Edição, LTC, 1996
Cap. 26 - Potencial
Elétrico
Física 2
Resnick, Halliday, Krane
4ª Edição, LTC, 1996
Cap. 30 - Potencial
Elétrico
Física 2
Resnick, Halliday, Krane
5ª Edição, LTC, 2003
Cap. 28 - Energia
Potencial Elétrica e
Potencial Elétrico
Prof. Anderson (Itacaré, BA - Fev/2006)
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
HALLIDAY, RESNICK, WALKER, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FUNDAMENTOS DE FÍSICA 3
CAPÍTULO 26 - POTENCIAL ELÉTRICO
EXERCÍCIOS E PROBLEMAS
01
11
21
31
41
51
61
71
81
91
02
12
22
32
42
52
62
72
82
92
03
13
23
33
43
53
63
73
83
93
04
14
24
34
44
54
64
74
84
94
05
15
25
35
45
55
65
75
85
95
06
16
26
36
46
56
66
76
86
96
07
17
27
37
47
57
67
77
87
97
08
18
28
38
48
58
68
78
88
98
09
19
29
39
49
59
69
79
89
99
10
20
30
40
50
60
70
80
90
100
[Início documento]
[Início seção]
[Início documento]
________________________________________________________________________________________________________
a
Cap. 26 – Potencial Elétrico
Halliday, Resnick, Walker - Física 3 - 4 Ed. - LTC - 1996.
2
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
CAPÍTULO 30 - POTENCIAL ELÉTRICO
PROBLEMAS
01
11
21
31
41
51
61
02
12
22
32
42
52
62
03
13
23
33
43
53
63
05
15
25
35
45
55
65
04
14
24
34
44
54
64
06
16
26
36
46
56
66
07
17
27
37
47
57
67
08
18
28
38
48
58
68
09
19
29
39
49
59
10
20
30
40
50
60
[Início documento]
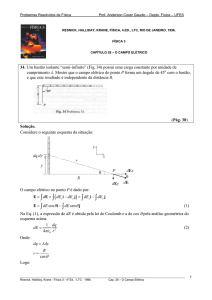
04. As cargas mostradas na Fig. 26 estão fixas no espaço. Encontre o valor da distância x tal que a
energia potencial elétrica do sistema seja nula.
(Pág. 72)
Solução.
Considere o esquema abaixo:
q1
q2
d
x
q3
Energia potencial elétrica nula:
1 qi q j
=0
U =∑
i < j 4πε 0 rij
1 ⎛ q1q2 q1q3 q2 q3 ⎞
+
+
⎜
⎟=0
4πε 0 ⎝ r12
r13
r23 ⎠
q1q2 q1q3 q2 q3
+
+
=0
d
x+d
x
q1q2 x 2 + ( q1q2 + q1q3 + q2 q3 ) x + q2 q3d = 0
Raízes de (1):
x1 = −0, 07823
x2 = 0, 20514
(1)
cm
cm
Como x é uma distância, deve ser maior do que zero. Logo:
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
3
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
x ≈ 20,5 cm
[Início seção]
[Início documento]
08. A diferença de potencial elétrico entre os pontos extremos de uma descarga elétrica durante uma
tempestade é 1,2 × 109 V. De quanto varia a energia potencial elétrica de um elétron que se
move entre esses pontos? Dê a sua resposta entre (a) joules e (b) elétron-volts.
(Pág. 72)
Solução.
A variação da energia potencial elétrica sofrida por um elétron para ir do ponto 1 ao ponto 2, ΔU12,
é dada pela Eq. (1), em que W12 é o trabalho realizado pela força elétrica que age sobre o elétron no
percurso 1 → 2.
ΔU12 = −W12
(1)
A diferença de potencial elétrico entre os pontos 1 e 2 é dada por (2), em que q0 é a carga
transportada no percurso 1 → 2.
W
ΔV12 = − 12
q0
(2)
Combinando-se (1) e (2) e substituindo-se q0 pela carga do elétron, e, teremos:
ΔU12 = q0 ΔV12 = eΔV12
ΔU12 = (1,60 ×10−19 C )(1, 23 ×109 V ) = 1,968 ×10−10 J
ΔU12 ≈ 1,97 ×10−10 J
1
eV ⎞
⎛
ΔU12 = (1,968 ×10−10 J ) ⎜
= 1, 2284
−19
J ⎟⎠
⎝ 1, 602 ×10
×109 eV
ΔU12 ≈ 1, 23 ×109 eV
[Início seção]
[Início documento]
13. Uma partícula de carga (positiva) Q está em uma posição fixa P. Uma segunda partícula, de
massa m e carga (negativa) −q se move com velocidade constante em um círculo de raio r1, com
centro em P. Deduza uma expressão para o trabalho W que precisa ser realizado por um agente
externo sobre a segunda partícula para aumentar o raio do círculo, centrado em P para r2.
(Pág. 72)
Solução.
Considere o esquema a seguir:
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
4
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
r2
v1
−
F1
Q +
q − F2
v2
r1
U1
U2
Quando a carga −q é transferida da órbita r1 para r2, há variação (positiva) de energia potencial
elétrica e (negativa) de energia cinética, ou seja, ocorre variação da energia mecânica do sistema.
Como este é conservativo, a variação da energia mecânica é causada pelo trabalho (W) de uma força
externa resultante, que desejamos determinar.
W = ΔE = E2 − E1 = ( K 2 + U 2 ) − ( K1 + U1 )
kQ ( −q ) ⎤ ⎡ 1 2 kQ ( −q ) ⎤
⎡1
W = ⎢ mv22 +
⎥ − ⎢ mv1 +
⎥
r2 ⎦ ⎣ 2
r1 ⎦
⎣2
⎛1
kQq ⎞ ⎛ 1 2 kQq ⎞
W = ⎜ mv22 −
⎟ − ⎜ mv1 −
⎟
r2 ⎠ ⎝ 2
r1 ⎠
⎝2
(1)
O movimento da carga −q na órbita circular de raio r é governado pela força de atração em relação
à carga Q. Essa força elétrica (F) age como força centrípeta (Fc). Logo:
F = Fc
kQq mv 2
=
r2
r
kQq
mv 2 =
r
Substituindo-se (2) em (1):
(2)
⎛ kQq kQq ⎞ ⎛ kQq kQq ⎞
kQq kQq
W =⎜
−
−
+
⎟−⎜
⎟=−
r2 ⎠ ⎝ 2r1
r1 ⎠
2r2
2r1
⎝ 2r2
W=
kQq ⎛ 1 1 ⎞
⎜ − ⎟
2 ⎝ r1 r2 ⎠
W=
Qq ⎛ 1 1 ⎞
⎜ − ⎟
8πε 0 ⎝ r1 r2 ⎠
Como r2 > r1, teremos W > 0. Ou seja, um agente externo deverá realizar trabalho positivo sobre o
sistema para levá-lo do estado 1 para o estado 2.
[Início seção]
[Início documento]
16. Uma placa infinita carregada tem densidade de carga σ = 0,12 μC/m2. A que distância estão as
superfícies equipotenciais cujos potenciais diferem de 48 V?
(Pág. 73)
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
5
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
Solução.
Considere o seguinte esquema da situação:
F
A
q0
B
d
ds
E
+ + + + + + + + + + + + + + + + +
O módulo do campo elétrico gerado por uma placa infinita, que possui densidade de carga
homogênea σ, é dado por:
E=
σ
2ε 0
Ou seja, o campo elétrico gerado por essa placa é constante. A diferença de potencial entre duas
superfícies equipotenciais A e B localizadas nas proximidades da placa, sendo que B está mais
próxima da placa, vale:
W
1 B
ΔVAB = VB − VA = − AB = − ∫ F.ds
q0
q0 A
ΔVAB = −
1
q0
∫
B
A
q0E.ds = − ∫ E.ds = − ∫ E.ds cos π = − E ∫ ds ( −1)
B
B
B
A
A
A
B
ΔVAB = E ∫ ds = Ed
A
Logo:
−12
2
2
ΔVAB ΔVAB 2ε 0 ΔVAB 2 ( 8,85 ×10 C /N.m ) ( 48 V )
=
=
=
= 7, 08 ×10−3 m
d=
−
6
2
σ
σ
E
( 0,12 ×10 C/m )
2ε 0
d ≈ 7,1 mm
[Início seção]
[Início documento]
18. Na experiência da gota de óleo de Millikan (veja Seção 28-6), um campo elétrico de 1,92 × 105
N/C é mantido entre duas placas separadas por 1,5 cm. Encontre a diferença de potencial entre
as placas.
(Pág. 73)
Solução.
Considere o seguinte esquema da situação, em que a carga de prova q0 será transportada da placa
negativa (A) para a placa positiva (B):
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
6
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
+ + + + + + + + + + + + + + + + + B
ds
E
d
q0
F
A
− − − − − − − − − − − − − − − −−
A diferença de potencial entre as placas corresponde ao negativo do trabalho realizado pelo campo
elétrico sobre uma carga de prova em seu movimento de uma placa à outra, dividido pela carga de
prova.
W
1 B
ΔVAB = VB − VA = − AB = − ∫ F.ds
q0
q0 A
ΔVAB = −
1
q0
∫
B
A
q0E.ds = − ∫ E.ds = − ∫ E.ds cos π = − E ∫ ds ( −1)
B
B
B
A
A
A
ΔVAB = E ∫ ds = Ed = (1,92 ×105 N/C ) ( 0, 015 m ) = 2.880 V
B
A
ΔVAB ≈ 2,9 kV
[Início seção]
[Início documento]
20. O campo elétrico dentro de uma esfera não-condutora de raio R, cuja densidade de carga é
uniforme, tem direção radial e seu módulo é
qr
E( r ) =
,
4πε 0 R3
sendo q a carga total na esfera e r a distância ao centro desta. (a) Determine o potencial V(r)
dentro da esfera, considerando V = 0 em r = 0. (b) Qual a diferença de potencial elétrico entre
um ponto da superfície e outro centro da esfera? Se q for positiva, que ponto possui maior
potencial? (c) Mostre que o potencial à distância r do centro, sendo r < R, é dado por
q 3R 2 − r 2
V=
8πε 0 R3
onde o zero do potencial foi arbitrado em r = ∞. Por que este resultado difere do que foi
apresentado no item (a)?
(Pág. 73)
(
)
Solução.
(a) Considere o esquema abaixo, em que os pontos C, S e P estão localizados no centro, na
superfície e no interior da esfera, a uma distância r do centro, respectivamente:
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
7
Problemas Resolvidos de Física
+
+
R
+
+
E
C
+
r
+
+
P S
ds = dr
+
+
Prof. Anderson Coser Gaudio – Depto. Física – UFES
+
+
A diferença de potencial entre os pontos P e C vale:
P
ΔVCP = VP − VC = − ∫ E.ds
C
Considerando o potencial nulo no centro da esfera, teremos:
r
r
r
0
0
0
VP − VC = V( r ) − 0 = − ∫ E.ds = − ∫ E.ds.cos 0 = − ∫ E.ds
Neste caso, como o valor de referência do potencial é no centro da esfera ( e não no infinito), os
vetores ds (deslocamento a partir do ponto de referência do potencial) e dr (deslocamento radial a
partir de r = 0) são idênticos (ds = dr)
V( r ) = −∫
r
0
r
qr
q
q r2
dr
rdr
=
−
=
−
4πε 0 R3
4πε 0 R3 ∫0
4πε 0 R3 2
qr 2
V( r ) = −
8πε 0 R3
(b) A diferença de potencial entre S e C vale:
qR 2
ΔVCS = VS − VC = V( R ) − V(0) = −
−0
8πε 0 R3
ΔVCS = −
q
8πε 0 R
Como ΔVCS é negativo, isto significa que indo do centro para a superfície da esfera o potencial
elétrico diminui se a carga da esfera for positiva. Logo, o centro da esfera apresenta maior potencial
(c) Com V = 0 no infinito, o cálculo de V(r) é feito da seguinte forma:
S
P
∞
S
VP − V∞ = − ∫ Eext .ds − ∫ Eint .ds
O cálculo deve ser feito em duas etapas, pois o comportamento do campo elétrico no interior da
esfera é diferente do comportamento no exterior.
S
P
V( r ) − 0 = − ∫ Eext .ds.cos180 − ∫ Eint .ds.cos180
∞
S
S
P
∞
S
V( r ) = ∫ Eext .ds + ∫ Eint .ds
Neste caso, como o valor de referência do potencial é no infinito, os vetores ds (deslocamento a
partir do ponto de referência do potencial) e dr (deslocamento radial a partir de r = 0) possuem
sentido contrário (ds = −dr).
R
r
1 q
qr
. ( −dr ) + ∫
. ( −dr )
V( r ) = ∫
∞ 4πε r 2
R 4πε R 3
0
0
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
8
Problemas Resolvidos de Física
V( r ) = −
q
4πε 0
∫
R
∞
Prof. Anderson Coser Gaudio – Depto. Física – UFES
dr
q
−
2
4πε 0 R3
r
∫
r
R
rdr
q ⎡ ⎛ 1 1 ⎞⎤
q ⎛ r 2 − R2 ⎞
V( r ) = −
−⎜ − ⎟ −
⎜
⎟
4πε 0 ⎢⎣ ⎝ R ∞ ⎠ ⎥⎦ 4πε 0 R3 ⎝ 2 ⎠
V( r ) =
1
q ⎛ r 2 − R2 ⎞
−
⎜
⎟
4πε 0 R 8πε 0 R ⎝ R 2 ⎠
q
Após o desenvolvimento da equação acima, a resposta será obtida.
V( r ) =
q ( 3R 2 − r 2 )
8πε 0 R3
O valor de V(r) obtido no item (a) difere do valor acima devido à mudança observada na posição de
referência onde V = 0.
[Início seção]
[Início documento]
28. Suponha que a carga negativa de uma moeda de cobre tenha sido removida para uma grande
distância da Terra - talvez uma galáxia distante - e que a carga positiva foi distribuída
uniformemente na superfície do nosso planeta. De quanto mudaria o potencial elétrico na
superfície da Terra? (Veja o Exemplo 2 no Cap. 27)
(Pág. 74)
Solução.
O planeta Terra apresenta um campo elétrico E de módulo igual a 150 N/C, que aponta diretamente
para baixo, ortogonalmente à sua superfície. Como a Terra pode ser considerada uma esfera
condutora, esse campo é gerado por uma distribuição de cargas negativas distribuídas
homogeneamente sobre sua superfície. Próximo à superfície do planeta, considerada plana, o campo
elétrico vale:
E=
Logo:
σ
ε0
σ = ε 0 E = ( 8,85 ×10−12 C2 /N ⋅ m2 ) (150 N/C ) = 1,3275 ×10−9 C/m2
A carga total sobre a superfície vale:
QT = −σ ⋅ 4π RT2 = (1,3275 ×10−9 C/m2 ) ⋅ 4π ( 6,37 ×106 m ) = −676.898,04…C
2
QT ≈ −6, 77 kC
O potencial elétrico na superfície e no exterior da Terra é o mesmo que seria produzido se a carga
QT fosse puntiforme e localizada no centro do planeta, ou seja:
1 q
V( r ) =
(r ≥ RT)
4πε 0 r
Na superfície, o potencial vale:
1 QT
V( RT ) =
4πε 0 RT
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
9
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
Portanto, mudanças na carga total da superfície do planeta acarretam variações no potencial elétrico
em sua superfície. A moeda de cobre citada no enunciado do problema, de massa igual a 3,11 g,
possui número de átomos de cobre igual a:
23
N A m ( 6, 02 ×10 átomos/mol ) ( 3,11 g )
=
= 2,9483
N=
M
( 63,5 g/mol )
×1022 átomos
Na expressão acima, NA é o número de Avogadro, m é a massa da moeda de cobre, fornecida no
Exemplo citado no enunciado, e M é a massa molar do cobre. A carga positiva presente na moeda
QM é igual ao produto de N, do número de prótons por átomo Z e da carga do próton +e:
QM = NZe = ( 2,9483 ×1022 ) ( 29 ) (1, 60 ×10−19 C ) = 1,3680
×105 C = 136,80
kC
Ao distribuir a carga QM sobre a superfície da Terra, o novo potencial será devido à carga Q = QT +
QM. Portanto, a variação no potencial elétrico será igual a:
⎛ 1 QT + QM
ΔV = VQ − VQT = ⎜
RT
⎝ 4πε 0
QM
ΔV =
=
4πε 0 RT
⎞ ⎛ 1 QT ⎞
1
( QT + QM − QT )
⎟−⎜
⎟=
R
R
πε
πε
4
4
T ⎠
0
0 T
⎠ ⎝
(1,3680
×105 C )
⎛
C ⎞
4π ⎜ 8,85 ×10−12
6,37 ×106 m )
2 ⎟(
N⋅m ⎠
⎝
2
= 1,9310
×108 V
ΔV ≈ 193 MV
[Início seção]
[Início documento]
35. Para a configuração de cargas da Fig. 35, mostre que V(r) para pontos no eixo vertical,
considerando r >> d, é dado por
1 q ⎛ 2d ⎞
V=
⎜1 +
⎟
4πε 0 r ⎝
r ⎠
(Sugestão: A configuração de cargas pode ser vista como a soma de uma carga isolada e um
dipolo.)
(Pág. 74)
Solução.
A forma mais direta de cálculo do potencial no ponto P devido às três cargas é por meio da soma
dos potenciais gerados por cada uma dessas cargas. Considerando-se no esquema acima como 1, 2 e
3 as cargas superior, do meio e inferior, teremos:
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
10
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
V = V1 + V2 + V3
V=
1
q
1 q
1
q
+
−
4πε 0 ( r − d ) 4πε 0 r 4πε 0 ( r + d )
V=
q ⎡ 1
1
1 ⎤
q ⎡ r ( r + d ) + ( r + d )( r − d ) − r ( r − d ) ⎤
+ −
⎢
⎥=
⎢
⎥
4πε 0 ⎣ ( r − d ) r ( r + d ) ⎦ 4πε 0 ⎣
r ( r + d )( r − d )
⎦
q ⎡ r 2 + 2rd − d 2 ⎤
(1)
⎥
⎢
4πε 0 ⎣ r ( r + d )( r − d ) ⎦
A Eq. (1) corresponde ao valor exato do potencial no ponto P gerado pelas três cargas. Para
obtermos a expressão do potencial para pontos onde r >> d, é preciso aproximar o denominador do
termo entre colchetes para r3, o que significa fazer r + d ≈ r e r − d ≈ r, e truncar em algum ponto a
soma que aparece no numerador do mesmo termo. Se o truncamento resultar em r2, o resultado será:
V=
q r2
1 q
V≈
=
3
4πε 0 r
4πε 0 r
(2)
A Eq. (2) corresponde ao potencial de apenas uma carga pontual q a uma distância r dessa carga.
Neste caso, percebemos que o truncamento foi exagerado, pois não existem traços da presença do
dipolo na expressão resultante. Aproximando-se o numerador do termo entre colchetes de (1) para
r2 + 2rd, teremos:
V≈
q ⎛ r 2 + 2rd ⎞
⎜
⎟
4πε 0 ⎝ r 3 ⎠
V≈
⎛ 2d ⎞
⎜1 +
⎟
4πε 0 r ⎝
r ⎠
q
Podemos também acatar a sugestão dada no enunciado do problema e considerar o potencial
elétrico no ponto P como sendo o resultado da sobreposição do potencial elétrico produzido pelo
dipolo (cargas das extremidades do arranjo) e potencial da carga central (+q).
V = Vdip + Vq
(3)
Na Seção 30.6 do livro, é feito o cálculo do potencial gerado por um dipolo, sendo que para r >> d,
o resultado é:
1 2qd cos θ
V≈
(4)
4πε 0
r2
Na Eq. (4), θ é o ângulo entre a linha que une as cargas do dipolo e a linha que une o centro do
dipolo ao ponto P. No presente caso, θ = 0. Substituindo-se (4) em (3), teremos:
1 2qd
1 q
V≈
+
2
4πε 0 r
4πε 0 r
V≈
1 q ⎛ 2d ⎞
⎜1 +
⎟
4πε 0 r ⎝
r ⎠
[Início seção]
[Início documento]
38. Uma quantidade total de carga positiva Q é espalhada sobre um anel circular plano de raio
interno a e raio externo b. A carga é distribuída de modo que a densidade de carga (carga por
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
11
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
unidade de área) é dada por σ = k/r3, onde r é a distância desde o centro do anel a qualquer
ponto deste. Mostre que o potencial no centro do anel é dado por
Q ⎛ a+b⎞
V=
⎜
⎟
8πε 0 ⎝ ab ⎠
(Pág. 75)
Solução.
Considere o esquema abaixo:
rdθ
dq
Q
dr
dθ
a
b
q
Elemento de carga no anel:
dq k
σ=
=
dA r 3
dq
k
= 3
rdrdθ r
kdrdθ
dq =
r2
Carga total no anel:
Q = ∫ dq
(1)
(2)
Substituindo-se (1) em (2):
b 2π dθ dr
Q = ∫ dq = k ∫ ∫
a 0
r2
⎛1 1⎞
Q = 2π k ⎜ − ⎟
⎝a b⎠
Potencial elétrico no centro do anel:
1 dq
dV =
4πε 0 r
V = ∫ dV =
1
4πε 0
∫
dq
r
(3)
Substituindo-se (1) em (3):
k b 2π dθ dr
V=
4πε 0 ∫a ∫0 r 3
V=
k ⎛ 1 1⎞
⎜ − ⎟
4ε 0 ⎝ a 2 b 2 ⎠
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
12
Problemas Resolvidos de Física
V=
Prof. Anderson Coser Gaudio – Depto. Física – UFES
k ⎛ 1 1 ⎞⎛ 1 1 ⎞ ⎛ 2π ⎞
⎜ − ⎟⎜ + ⎟ × ⎜
⎟
4ε 0 ⎝ a b ⎠⎝ a b ⎠ ⎝ 2π ⎠
⎡
⎛ 1 1 ⎞⎤ 1 ⎛ 1 1 ⎞
V = ⎢ 2π k ⎜ − ⎟ ⎥
⎜ + ⎟
⎝ a b ⎠ ⎦ 8πε 0 ⎝ a b ⎠
⎣
O termo entre colchetes é a carga total Q:
V=
Q ⎛1 1⎞
⎜ + ⎟
8πε 0 ⎝ a b ⎠
[Início seção]
[Início documento]
40. O campo elétrico realiza trabalho de 3,94 × 10-19 J sobre um elétron no campo ilustrado na Fig.
37, para mover o elétron desde A até B, ao longo de uma linha de campo. Quais as diferenças de
potencial elétrico (a) VB − VA, (b) VC − VA e (c) VC − VB?
(Pág. 75)
Solução.
(a)
ΔVAB = VB − VA = −
( 3,94 ×10−19 J ) = 2, 4625 V
WAB
W
= − AB = −
q0
e
(1,60 ×10−19 C)
ΔVAB ≈ 2, 46 V
(b) Neste caso, o elétron é transportado entre as mesmas superfícies equipotenciais do item (a).
Logo:
ΔVAC = ΔVAB ≈ 2, 46 V
(c) Como o elétron permanece na mesma superfície equipotencial, não há variação de potencial
elétrico.
ΔVBC = 0
[Início seção]
[Início documento]
51. Em um bastão fino de comprimento L, que está sobre o eixo x, com uma extremidade na origem
(x = 0), como na Fig. 42, está distribuída uma carga por unidade de comprimento dada por λ =
kx, sendo k uma constante. (a) Considerando nulo o potencial eletrostático no infinito, determine
V no ponto P do eixo y. (b) Determine a componente vertical Ey do campo elétrico em P,
utilizando o resultado de (a) e também por cálculo direto. (c) Por que a componente horizontal
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
13
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
Ex do campo elétrico em P não pode ser encontrada usando o resultado de (a)? A que distância
do bastão, ao longo do eixo y, o potencial é igual à metade do seu valor na extremidade
esquerda do bastão?
(Pág. 76)
Solução.
Considere o esquema abaixo:
y
dE θ
P
θ
r
y
dq
x
x
dx
(a) Elemento de potencial (dV) gerado pelo elemento de carga (dq):
1 dq
1
dq
dV =
=
4πε 0 r 4πε 0 y 2 + x 2 1/ 2
(
)
Elemento de carga (dq):
dq
λ=
= kx
dx
dq = kxdx
(1)
(2)
Substituindo-se (2) em (1):
k
xdx
dV =
4πε 0 ( y 2 + x 2 )1/ 2
V = ∫ dV =
V=
V=
k
4πε 0
k
4πε 0
(y
2
∫
xdx
L
(y
0
+ x2 )
2
+ x2 )
1/ 2
1/ 2 L
0
k ⎡ 2 2 1/ 2
( y + L ) − y ⎤⎥⎦
4πε 0 ⎢⎣
(b)
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
14
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
Ey = −
∂V
∂ ⎧ k ⎡ 2 2 1/ 2
⎤ ⎫⎬
y
=− ⎨
+
−
L
y
(
)
⎦⎥ ⎭
∂y
∂y ⎩ 4πε 0 ⎣⎢
Ey = −
k ⎡ 1 2 2 −1/ 2
⎤
y + L ) .2 y − 1⎥
(
⎢
4πε 0 ⎣ 2
⎦
Ey =
⎡
⎤
k ⎢
y
⎥
1−
4πε 0 ⎢ ( y 2 + L2 )1/ 2 ⎥
⎣
⎦
Cálculo direto de V
dE = −dE sen θ i + dE cosθ j
(3)
Módulo do elemento de campo elétrico:
1 dq
dE =
4πε 0 r 2
(4)
Substituindo-se (2) em (4):
k
xdx
dE =
2
4πε 0 y + x 2
(5)
Senos e cossenos de θ:
x
sen θ =
1/ 2
( y 2 + x2 )
cosθ =
(7)
y
(8)
( y2 + x2 )
1/ 2
Substituindo-se (5), (6) e (7) em (3):
dE = −
x 2 dx
k
4πε 0 ( y + x
2
E = ∫ dE = −
k
4πε 0
∫
)
2 3/ 2
L
0
i+
ky
xdx
j
2
4πε 0 ( y + x 2 )3/ 2
x 2 dx
( y2 + x
)
2 3/ 2
i+
ky
4πε 0
∫
L
0
xdx
( y 2 + x2 )
3/ 2
j
2
2 1/ 2 ⎤
⎧ ⎡
⎫
k ⎪ ⎢L +(L + y ) ⎥
L
ky
⎪
−
E=−
i+
⎨ln
⎬
1/
2
⎥ ( y 2 + L2 ) ⎪ 4πε 0
y
4πε 0 ⎪ ⎢
⎦
⎩ ⎣
⎭
⎡
⎤
y
⎢1 −
⎥j
⎢ ( y 2 + L2 )1/ 2 ⎥
⎦
⎣
Nesta expressão, pode-se ver que :
Ey =
⎡
⎤
k ⎢
y
⎥
1−
1/ 2
2
2
⎢
⎥
4πε 0
⎣ (y +L ) ⎦
(c) Não há dependência de V em relação a x na resposta do item (a).
(d) Potencial na extremidade esquerda do bastão, usando a resposta do item (a), com y = 0:
k ⎡ 2 2 1/ 2 ⎤
kL
V(0) =
0 +L
− 0⎥ =
⎢
⎦ 4πε 0
4πε 0 ⎣
(
)
Valor de y para o qual V(y) = V(0)/2:
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
15
Problemas Resolvidos de Física
V( y ) =
V(0)
2
=
Prof. Anderson Coser Gaudio – Depto. Física – UFES
kL
8πε 0
k ⎡ 2 2 1/ 2
kL
y + L ) − y ⎤⎥ =
(
⎢
⎣
⎦
4πε
8πε
0
(y
2
y=
+ L2 )
1/ 2
−y=
0
L
2
3L
4
[Início seção]
[Início documento]
55. Uma carga de 15 nC pode ser produzida por simples atrito. Que variação de potencial essa carga
causará em uma esfera condutora isolada de 16 cm de raio?
(Pág. 76)
Solução.
A variação de potencial elétrico que a esfera de raio r sofrerá vale:
ΔV = V − V0 ,
onde V0 é o potencial da esfera na ausência de cargas elétricas em sua superfície (V0 = 0) e V é o
potencial na superfície da esfera carregada homogeneamente com carga q. O potencial V é o mesmo
que se verifica a uma distância r de uma carga puntiforme.
1 q
ΔV =
=
4πε 0 r
(1,5 ×10
1
−8
C)
= 842,58
⎛
C ⎞ ( 0,16 cm )
−12
4π ⎜ 8,85 ×10
⎟
N.m 2 ⎠
⎝
Apresentando-se a resposta com dois algarismos significativos:
ΔV ≈ 840 V
2
[Início seção]
V
[Início documento]
56. Encontre (a) a carga e (b) a densidade de carga na superfície de uma esfera condutora de 15,2
cm de raio, cujo potencial é de 215 V.
(Pág. 76)
Solução.
(a) O potencial elétrico no exterior de uma esfera condutora de raio R e carga q é dado por:
1 q
V( r ) =
(r ≥ R)
4πε 0 r
Conhecendo-se V(R), pode-se calcular q:
1 q
V( R ) =
4πε 0 R
⎛
C2 ⎞
q = 4πε 0 RV( R ) = 4π ⎜ 8,85 ×10−12
⎟ ( 0,152 m )( 215 V ) = 3, 6344
N ⋅ m2 ⎠
⎝
×10−9 C
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
16
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
q ≈ 3,63 nC
(b) A densidade superficial de carga σ vale:
3,6344 ×10−9 C )
(
q
q
σ= =
=
= 1, 2518
2
A 4π R 2
4π ( 0,152 m )
×10−8 C/m2
σ ≈ 12,5 nC/m 2
[Início seção]
[Início documento]
________________________________________________________________________________________________________
a
Cap. 30 – Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
17
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 5.ED., LTC, RIO DE JANEIRO, 2003.
FÍSICA 3
CAPÍTULO 28 - ENERGIA POTENCIAL ELÉTRICA E POTENCIAL ELÉTRICO
EXERCÍCIOS
01
11
21
31
41
02
12
22
32
42
03
13
23
33
43
04
14
24
34
44
05
15
25
35
45
06
16
26
36
46
07
17
27
37
47
08
18
28
38
48
09
19
29
39
49
10
20
30
40
50
07
17
27
37
47
08
18
28
38
48
09
19
29
39
49
10
20
30
40
50
PROBLEMAS
01
11
21
31
41
02
12
22
32
42
03
13
23
33
43
04
14
24
34
44
05
15
25
35
45
06
16
26
36
46
[Início documento]
[Início seção]
[Início documento]
________________________________________________________________________________________________________
a
Cap. 28 – Energia Potencial Elétrica e Potencial Elétrico
Resnick, Halliday, Krane - Física 3 - 5 Ed. - LTC - 2003.
18