Gravitação Universal

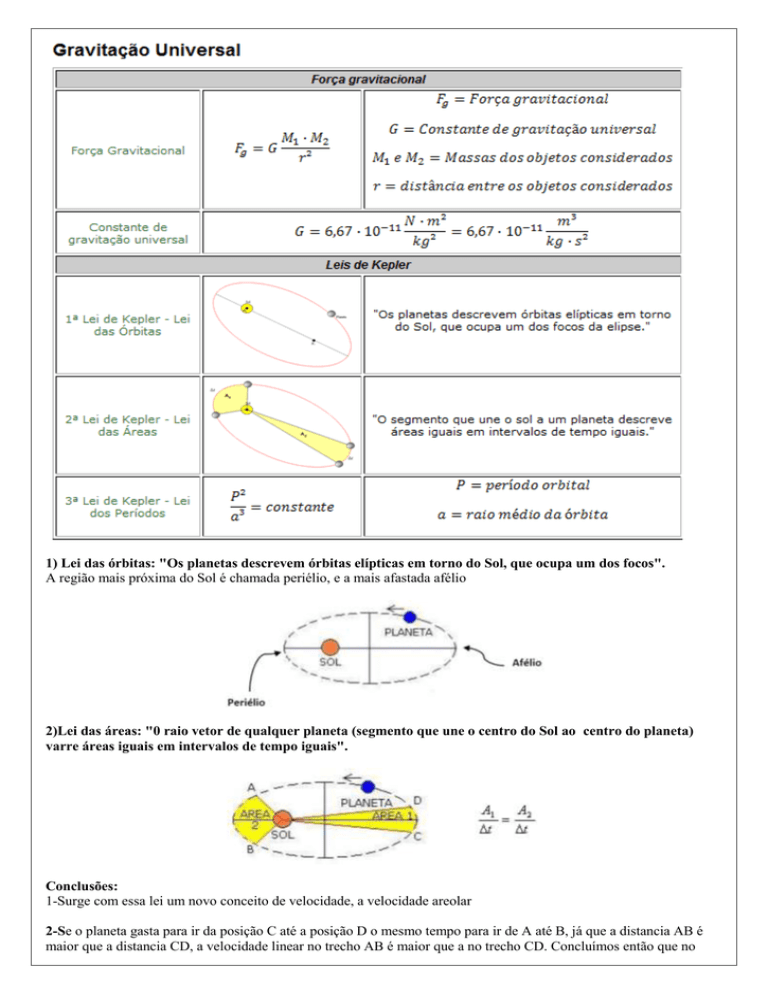
1) Lei das órbitas: "Os planetas descrevem órbitas elípticas em torno do Sol, que ocupa um dos focos".
A região mais próxima do Sol é chamada periélio, e a mais afastada afélio
2)Lei das áreas: "0 raio vetor de qualquer planeta (segmento que une o centro do Sol ao centro do planeta)
varre áreas iguais em intervalos de tempo iguais".
Conclusões:
1-Surge com essa lei um novo conceito de velocidade, a velocidade areolar
2-Se o planeta gasta para ir da posição C até a posição D o mesmo tempo para ir de A até B, já que a distancia AB é
maior que a distancia CD, a velocidade linear no trecho AB é maior que a no trecho CD. Concluímos então que no
periélio movimento do planeta é mais rápido do que quando o planeta está no afélio. Ou seja, os planetas giram mais
depressa quando estão mais perto do Sol e mais lentamente quando estão mais longe.
Isto foi explicado mais tarde por Newton e acontece porque, quando um planeta se encontra mais perto do Sol sofre
uma força de atração maior do que quando se encontra mais longe.
3-Em trajetórias circulares, a velocidade linear é constante.
4-A energia cinética de translação aumenta do afélio para o periélio, e diminui em sentido oposto. A energia potencial
gravitacional varia de maneira oposta.
3)Lei dos períodos: "Os quadrados dos períodos de revolução dos planetas são proporcionais aos cubos dos
semi-eixos maiores das respectivas órbitas".
Esta lei diz-nos que quanto mais afastado do Sol estiver o planeta mais tempo demora a dar uma volta completa ao
mesmo. Por exemplo, a terra que está a 1UA do Sol (1unidade astronômica = distância media entre o Sol e a Terra =
150 x106Km) demora um ano a dar uma volta completa ao Sol enquanto o planeta mais afastado do Sol (Plutão)
demora 248 Anos terrestres a dar uma volta completa ao Sol e o raio da sua órbita é de 39,4 UA.
T2 / R3 = K (constante)
Onde:
T: período de revolução do planeta
R: raio da órbita do planeta
Considere por exemplo, dois planetas como a Terra e Vênus. Esses dois planetas descrevem trajetórias quase
circulares em torno do Sol e completam uma volta em um intervalo de tempo chamado ano do planeta, ou período de
translação.
Para o caso particular da Terra e de Vênus, se aplicarmos a lei dos períodos, teremos a seguinte relação matemática:
Obs. As três leis de Kepler são válidas para quaisquer sistemas em que corpos gravitam em torno de um corpo
central. Exemplos: planetas em torno de uma estrela, Lua em torno da Terra, satélites artificiais em torno da
Terra.
A Lei da Gravitação Universal é uma expressão matemática baseada na força de atração do Sol nos planetas cujo
enunciado é:
“Dois corpos quaisquer se atraem com uma força proporcional ao produto das suas massas e inversamente
proporcional ao quadrado da distância que os separa ."
É expressa matematicamente por:
F = (G.m1.m2) / d2
Onde:
F: força de atração
G: constante de gravitação universal
m1 e m2: massas dos corpos estudados
d: distância entre os corpos
Esta lei estabelece duas relações importantes:
1-Quanto maior a distância entre dois corpos, menor a força de atração, e vice-versa.
2-Quanto maior as massas dos corpos, maior a força de atração, e vice-versa.
A força F1 de atração que o Sol exerce sobre o planeta é maior que F2 porque a distância que o planeta está do Sol na
posição 1 é menor que a distância na posição 2.
Observações Importantes:
1ª) A força gravitacional é sempre de atração
2ª) A força gravitacional não depende do meio onde os corpos se encontram imersos.
3ª) A constante da gravitação universal G teve seu valor comprovado experimentalmente por Henry Cavendish por
meio de um instrumento denominado balança de torção.
_____________________________________________________________________________________________
tem período T/3. Qual o raio da órbita do segundo
satélite?
Exercício resolvido: Gravitação Universal
Exercício de física resolvido. Questão que exige
conhecimentos de astronomia: Gravitação Universal.
(Gravitação Universal) A respeito do planeta júpiter e
de um de seus satélites, Io, foram feitas as afirmações:
I. Sobre esses corpos celestes, de grandes, de grandes
massas, predominam as forças gravitacionais.
II. É a força de Júpiter em Io que o mantém em órbita
em torno do planeta.
III. A força que Júpiter exerce em Io tem maior
intensidade que a força exercida por Io em Júpiter.
Deve-se concluir que somente:
a) I é correta. b) II é correta. c) III é correta.
e II são corretas. e) II e III são corretas.
d) I
Resolução
I. Correta: De acordo com a lei da gravitação, verificase que as forças gravitacionais são predominantes em
relação a corpos de grande massa.
II. Correta: A força gravitacional faz o papel de
resultante centrípeta.
III. Falsa. As forças têm a mesma intensidade.
Resposta do exercício: alternativa d.
Questões - Gravitação Universal
Leis de Kepler
(1) Um satélite de comunicação em órbita circular tem
raio R e período T. Um outro satélite de órbita circular
Gravitação Universal
(1) Qual a intensidade do campo gravitacional da Terra
sobre a Lua?
Dados:
Resolução:
04- O planeta Marte está a uma distância média igual a
2,3 · 108 km do Sol. Sendo 6,4 · 1023 kg a massa de
Marte e 2,0 · 1030 kg a massa do Sol, determine a
intensidade da força com que o Sol atrai Marte. Dados:
G = 6,67 · 10-11 Nm²/kg².
Dados:
d = 2,3 · 108 km,
m1 = 6,4 · 1023 kg
m2 = 2,0 · 1030 kg