tensão sinal -aplicação

Electrónica Geral
Mestrado Integrado em Engenharia Biomédica
Ano Lectivo 2013/2014
Relatório do Trabalho de Laboratório nº1
Transístores Metal-Óxido
Semicondutor
Inversor CMOS
elaborado a 29 /.Março./ 2013
Grupo

Turma
2ª feira 15h
2ª feira 17h
2
5ª feira 16h30
X
Apague os números que não correspondem ao seu grupo e coloque um X na sua Turma.
Número
Nome
72965
José Pedro Portela
73725
Raquel Maria Calçada
73716
Nuno Laurentino Mendes
Rubrica
Coloque os elementos do grupo por ordem numérica crescente.
Recebido........./..................../ 2014 às …….h…….m
por ……………………………………………….. (rúbrica)
Índice Remissivo
I Introdução Teórica ...................................................................................................................... 3
II Análise Teórica ........................................................................................................................... 4
Pergunta II – 1 ........................................................................................................................... 5
Pergunta II – 2 ......................................................................................................................... 11
Pergunta II – 3 ......................................................................................................................... 12
III Trabalho de Simulação ............................................................................................................ 14
Simulação em LT Spice ............................................................................................................ 14
Pergunta III – 1 ........................................................................................................................ 15
Pergunta III – 2 ........................................................................................................................ 17
Pergunta III – 3 ........................................................................................................................ 19
Pergunta III – 4 ........................................................................................................................ 22
IV Trabalho Experimental ............................................................................................................ 27
Pergunta IV – 1 – Análise das tensões de entrada e de saída; característica vO(vI) ................ 27
Pergunta IV – 2 – Análise dos tempos de subida, descida e de atraso de propagação do
inversor ................................................................................................................................... 29
Pergunta IV – 3 (facultativa) – Dispersão de Fabrico ............................................................. 32
Conclusões .................................................................................................................................. 37
Bibliografia .................................................................................................................................. 39
2
I Introdução Teórica
O transístor Metal Oxide Semiconductor Field-Effect Transistor (MOSFET) é o tipo de transístor
que se irá utilizar neste trabalho experimental. Este transístor é muito comum, sendo utilizado
tanto para circuitos analógicos como para digitais. A sua designação deve-se ao facto do estado
de corte ou condução ser determinado pelo campo eléctrico no seu interior. [1,2]
O transístor MOS tem a estrututra apresentada na figura em baixo (mais especificamente a
figura representa um transístor NMOS ou do tipo npn). O transístor assenta num cristal de
material semicondutor de tipo p, a que se desgina substrato (B – body, por estar normalmente
ligado ao ground despreza-se), onde existem duas regiões de tipo n+ (um material semicondutor
de tipo n com elevada concentração de substâncias que conferem este carácter ao material), o
dreno (D – drain) e a fonte (S – source). Entre estas duas regiões existe uma fina camada isolante
de óxido de silício (SiO2), e sobre esta, encontra-se uma camada de material condutor que
constitui a porta (G – gate), que pode ser de metal. Muitas vezes consideram-se somente 3
terminais, isto porque o substrato liga-se normalmente à fonte (B=S).
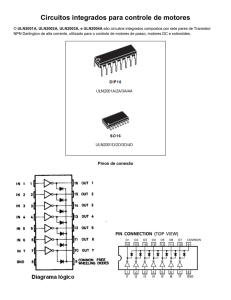
1
1. Dreno
2. Source
3. Gate
3
2
1
Figura 1 - Transístor MOS (mais especificamente NMOS)
Entre o dreno e a fonte ocorre passagem de corrente face à presença de uma tensão entre a
porta e a fonte (vGS), que seja superior à tensão de limiar Vt. Com isto, forma-se um canal sob o
óxido devido ao efeito de campo.
A presença de óxido isolante sobre a porta leva a que este terminal não seja percorrido por
corrente (iG=0). Desta forma: iB=iS. [3]
No transístor PMOS, basicamente existe uma troca dos materiais p e n, ou seja, o substrato é
composto por material de tipo n enquanto o dreno e a fonte são do tipo p+.
Figura 2 - Representação esquemática dos transístores npn à
esquerda (NMOS) e pnp à direita (PMOS)
3
Os transístores NMOS e PMOS operam nas seguintes regiões de funcionamento: [4]
O parâmetro que figura nas equações exprime-se em AV-2, e é igual a:
1
𝑊
𝐾 = 𝜇C𝑜𝑥
2
𝐿
Para o trabalho experimental, os valores usados encontram-se apresentados em baixo:
VTon
1.6V
-VTop
1.8V
VDD
13V
VSS
0V
II Análise Teórica
Este trabalho tem como objetivo o estudo de transístores Metal-Óxido-Semicondutor (MOS –
HEF 4007), mais especificamente o inversor CMOS.
VDD
4
T2
vI
𝑉𝑇𝑂𝑁 = 1.6𝑉 = 𝑉𝑡𝑁
−𝑉𝑇𝑂𝑃 = 1.8𝑉 ⇒ |𝑉𝑇𝑂𝑃 | = 1.8𝑉 = |𝑉𝑡𝑃 |
𝑉𝐷𝐷 = 13𝑉
𝑉𝑆𝑆 = 0𝑉 (𝑔𝑟𝑜𝑢𝑛𝑑)
𝐾𝑉𝐿: 𝑣𝐺𝐷 = 𝑣𝐺𝑆 − 𝑣𝐷𝑆
Figura 3 - Circuito inversor CMOS
Pergunta II – 1
- Traço da curva de transferência 𝑣𝑂 (𝑣𝐼 ), em que 𝑣𝑂 é a tensão de saída e 𝑣𝐼 a tensão de entrada.
- Identificação das cinco regiões de funcionamento do inversor CMOS.
O circuito CMOS tem dois MOS complementares em fonte comum em totem. Possui polarização
de porta: a componente contínua de 𝑣𝐼 (𝑉𝐼 – valor médio) é que polariza em DC.
Algumas expressões utilizadas:
𝐾𝑃 = 𝜇𝑂 𝐶𝑂𝑋
𝑘=
𝐾𝑃 𝑊
2 𝐿
𝑉𝑡 = 𝑉𝑇𝑂
Apesar das várias combinações possíveis, apenas teremos em conta as denotadas com o sinal
de correto, o que perfaz o total das 5 zonas:
NMOS





Corte
Tríodo
Saturação
Tríodo
Saturação
Tríodo
Corte
Saturação
Corte
PMOS





Tríodo
Corte
Tríodo
Saturação
Saturação
Tríodo
Corte
Corte
Saturação
Cálculo de k
Transístor NMOS: KP=73u; W=100u; L=5u (u significa 𝜇 de micro)
𝐾𝑃 𝑊 73 100
𝑘𝑁 = ( ) =
∗
= 730𝑢 = 7.3 ∗ 10−4 𝐴𝑉 −2
2 𝐿
2
5
5
Transístor PMOS: KP=16u; W=300u; L=5u
𝐾𝑃 𝑊 16 300
𝑘𝑃 = ( ) =
∗
= 480𝑢 = 4.8 ∗ 10−4 𝐴𝑉 −2
2 𝐿
2
5
Regiões de Funcionamento
ZONA 1: NMOS cortado (OFF) e PMOS em tríodo (ON)
𝟎 < 𝒗𝑰 < 𝑽𝒕𝑵 ⇒ 𝟎 < 𝒗𝑰 < 𝟏. 𝟔 (𝑽)
𝑣𝐼 = 0 ⇒ 𝑣𝐺𝑆𝑁 = 𝑣𝐼 = 0 < 𝑉𝑡𝑁 = 1.6𝑉
𝒊𝑫𝑵 = 𝒊𝑫𝑷 = 𝟎𝑨
𝒗𝑶 = 𝑽𝑫𝑫 = 𝒗𝑺𝑮𝑷 = 𝟏𝟑𝑽
𝑣𝐺𝑆𝑃 < 𝑉𝑡𝑃 ⇒ 𝑣𝐺𝑆𝑃 = −𝑉𝐷𝐷 = −13𝑉 < 𝑉𝑡𝑃 = −1.8𝑉
Figura 4 - Zona 1
𝑣𝐺𝐷𝑃 < 𝑉𝑡𝑃
𝑣𝐷𝑆𝑃 = 0 ⇒ 𝑣𝑂 = 𝑣𝐷𝑆𝑁 = 𝑉𝐷𝐷 + 𝑣𝐷𝑆𝑃 ≅ 𝑉𝐷𝐷 = 13𝑉
𝑣𝐺𝐷𝑃 = 𝑣𝐺𝑆𝑃 − 𝑣𝐷𝑆𝑃 = −(𝑉𝐷𝐷 + 𝑣𝐷𝑆𝑃 )
2 ]
𝑖𝐷𝑃 ≈ 𝑘𝑃 [2(𝑣𝐺𝑆𝑃 + 𝑉𝑡𝑃 )𝑣𝐷𝑆𝑃 − 𝑣𝐷𝑆𝑃
= 0 (𝑡𝑟í𝑜𝑑𝑜)
ZONA 2: NMOS saturado (ON) e PMOS em tríodo (ON)
Para que os dois MOS possam estar ON:
𝑉𝐷𝐷 > 𝑉𝑡𝑁 + |𝑉𝑡𝑃 | ⇒ 13 > 1.6 + 1.8 ⟺ 13 > 3.4
Em geral tenta-se ter 𝑘𝑁 = 𝑘𝑃 e 𝑉𝑡𝑁 = −𝑉𝑡𝑃 , devido à simetria. Contudo, não é o caso:
730 ≠ 480 e 1.6 ≠ 1.8
𝑽𝒕𝑵 < 𝒗𝑰 < 𝒗𝑶 − |𝑽𝒕𝑷 | ⇒ 𝟏. 𝟔 < 𝒗𝑰 < 𝒗𝑶 − 𝟏. 𝟖 ⟹ 𝟏. 𝟔 < 𝒗𝑰 < 𝟓. 𝟖𝟗𝟖𝟕 (𝑽) (𝒛𝒐𝒏𝒂 𝑨𝑩)
𝑣𝑂 − 1.8 = 7.6747 − 1.8 = 5.8987𝑉
𝒗𝑰 = 𝒗𝑮𝑺𝑵 ≥ 𝑽𝒕𝑵 (útil mais tarde na determinação do VtN através do catálogo)
𝑣𝑂 = 𝑣𝐷𝑆𝑁 ≥ 𝑣𝐼 − 𝑉𝑡𝑁
𝑣𝐷𝐺𝑃 = 𝑣𝑂 − 𝑣𝐼 > |𝑉𝑡𝑃 | ⇒ 𝑣𝑆𝐺𝑃 = 𝑉𝐷𝐷 − 𝑣𝐼 > |𝑉𝑡𝑃 | ⟺ 𝒗𝑰 < 𝑽𝒕𝑷 + 𝑽𝑫𝑫 = −1.8 + 13 =
11.2𝑉 (útil mais tarde na determinação do VtP através do catálogo)
No limite desta zona:
𝑣𝐼 = 𝑉𝑡𝑁 ⇒ 𝑣𝑂 = 𝑉𝐷𝐷 = 𝑣𝐷𝑆𝑁
𝑣𝑆𝐷𝑃 = 0
𝑖𝐷𝑁 = 𝑘𝑁 (𝑣𝐼 − 𝑉𝑡𝑁 )2
2 ]
𝑖𝐷𝑃 = 𝑘𝑃 [2(𝑉𝐷𝐷 − 𝑣𝐼 − |𝑉𝑡𝑃 |)(𝑉𝐷𝐷 − 𝑣𝑂 ) − (𝑉𝐷𝐷 − 𝑣𝑂 )2 ] = 𝑘𝑃 [2(𝑣𝑆𝐺𝑃 − |𝑉𝑡𝑃 |)𝑣𝑆𝐷 − 𝑣𝑆𝐷
𝑣𝑆𝐷 = 𝑉𝐷𝐷 − 𝑣𝑂
6
A equação 𝑣𝑂 (𝑣𝐼 ) é obtida ao igualar 𝑖𝐷𝑁 a 𝑖𝐷𝑃 , através do programa Wolfram Mathematica.
Assim, conseguiu-se determinar que:
𝒗𝟎 = 𝟕. 𝟔𝟕𝟒𝟕 V
Mantém-se nesta zona até 𝑣𝐼 = 𝑣𝑂 − |𝑉𝑡𝑃 | ⇒ 𝑣𝐷𝐺𝑃 = |𝑉𝑡𝑃 | quando PMOS satura.
ZONA 3: NMOS e PMOS em saturação (ON)
𝒗𝑶𝑨𝑩 − |𝑽𝒕𝑷 | < 𝒗𝑰 < 𝒗𝑶𝑪𝑫 + 𝑽𝒕𝑵 (𝒛𝒐𝒏𝒂 𝑩𝑪)
𝑖𝐷𝑁 = 𝑘𝑁 (𝑣𝐼 − 𝑉𝑡𝑁 )2
𝑖𝐷𝑃 = 𝑘𝑃 (𝑉𝐷𝐷 − 𝑣𝐼 − |𝑉𝑡𝑃 |)2 = 𝑘𝑃 (𝑣𝑆𝐺𝑃 − |𝑉𝑡𝑃 |)2
𝑣𝐺𝑆𝑁 = 𝑣𝐼
𝑣𝑆𝐺𝑃 = 𝑉𝐷𝐷 − 𝑣𝐼
Ao igualar 𝑖𝐷𝑁 a 𝑖𝐷𝑃 , através do programa Wolfram Mathematica, obtém-se um valor de 𝑣𝐼
constante. Na representação gráfica corresponde a um troço de recta vertical, com ganho
infinito.
Com base nos valores dados:
𝒗𝒊 = 𝟓. 𝟖𝟗𝟖𝟕𝑽
Obtém-se também a região de valores de 𝑣𝑂 :
𝑣𝑂𝐴𝐵 − |𝑉𝑡𝑃 | < 𝑣𝐼 < 𝑣𝑂𝐶𝐷 + 𝑉𝑡𝑁 ⇒ 𝒗𝒊 − 𝑽𝒕𝑵 < 𝒗𝟎 < 𝒗𝒊 + |𝑽𝒕𝑷 |
𝟒. 𝟐𝟗𝟖𝟕 < 𝒗𝟎 < 𝟕. 𝟔𝟗𝟖𝟕 (𝑽)
Se os transístores tiverem parâmetros idênticos (𝑘𝑃 = 𝑘𝑁 e 𝑉𝑡𝑁 = 𝑉𝑡𝑃 ) a característica é
simétrica e 𝑣𝐼 =
𝑉𝐷𝐷
.
2
Contudo, não se trata deste caso.
ZONA 4: NMOS em tríodo (ON) e PMOS em saturação (ON)
𝒗𝑶 + 𝑽𝒕𝑵 < 𝒗𝑰 < 𝑽𝑫𝑫 − |𝑽𝒕𝑷 | ⇒ 𝟓. 𝟖𝟗𝟖𝟕 < 𝒗𝑰 < 𝟏𝟏. 𝟐 (𝑽) (𝒛𝒐𝒏𝒂 𝑪𝑫)
Considerou-se 𝑣𝐼 = 5.8987𝑉 como o limite inferior para existir continuidade na função.
𝑣𝐼 < 𝑉𝐷𝐷 − |𝑉𝑡𝑃 | ⇒ 𝑣𝑆𝐺𝑃 > |𝑉𝑡𝑃 | ⇒ 𝑣𝐺𝑆𝑃 < 𝑉𝑡𝑃
𝑣𝐺𝐷𝑁 = 𝑣𝐼 − 𝑣𝑂 > 𝑉𝑡𝑁 ⇒ 𝑣𝐼 = 𝑣𝐺𝑆𝑁 > 𝑉𝑡𝑁
𝑣𝐷𝑆𝑁 = 𝑣𝑂 < 𝑣𝐼 − 𝑉𝑡𝑁
𝑣𝐷𝑆𝑃 < 𝑣𝐺𝑆𝑃 − 𝑉𝑡𝑃 ⇒ 𝑣𝑂 < 𝑣𝐼 − 𝑉𝑡𝑃
No limite desta zona:
𝑣𝐼𝑚𝑎𝑥 = 𝑉𝐷𝐷 − |𝑉𝑡𝑃 | ⇒ 𝑣𝑂 = 0 = 𝑣𝐷𝑆𝑁
𝑣𝑆𝐷𝑃 = 𝑉𝐷𝐷
7
𝑖𝐷𝑃 = 𝑘𝑃 (𝑉𝐷𝐷 − 𝑣𝐼 − |𝑉𝑡𝑃 |)2 = 𝑘𝑃 (𝑣𝑆𝐺𝑃 − |𝑉𝑡𝑃 |)2
𝑣𝑆𝐺𝑃 = 𝑉𝐷𝐷 − 𝑣𝐼
2 ]
𝑖𝐷𝑁 = 𝑘𝑁 [2(𝑣𝐼 − 𝑉𝑡𝑁 )𝑣𝑂 − 𝑣𝑂2 ] = 𝑘𝑁 [2(𝑣𝐺𝑆𝑁 − 𝑉𝑡𝑁 )𝑣𝐷𝑆𝑁 − 𝑣𝐷𝑆𝑁
𝑣𝐺𝑆𝑁 = 𝑣𝐼
𝑣𝐷𝑆𝑁 = 𝑣𝑂
A equação 𝑣𝑂 (𝑣𝐼 ) é obtida ao igualar 𝑖𝐷𝑁 a 𝑖𝐷𝑃 , através do programa Wolfram Mathematica.
O limite inferior desta zona é 𝑣𝐺𝐷𝑁 = 𝑣𝐼 − 𝑣𝑂 = 𝑉𝑡𝑁 ⇒ 𝑣𝐼 = 𝑣𝑂 + 𝑉𝑡𝑁 quando NMOS satura.
ZONA 5: NMOS em tríodo (ON) e PMOS cortado (OFF)
𝑖𝐷 = 0𝐴
𝑽𝑫𝑫 − |𝑽𝒕𝑷 | < 𝒗𝑰 < 𝑽𝑫𝑫 ⇒ 𝟏𝟏. 𝟐 < 𝒗𝑰 < 𝟏𝟑 (𝑽)
𝑣𝐼 = 𝑉𝐷𝐷 ⇒ 𝑣𝑆𝐺𝑃 = 0 < |𝑉𝑡𝑃 |
𝑣𝐺𝑆𝑁 = 𝑉𝐷𝐷 > 𝑉𝑡𝑁
𝑣𝐺𝑆𝑃 = 𝑣𝐼 − 𝑉𝐷𝐷 > 𝑉𝑡𝑃
𝑣𝑂 = 𝑣𝐷𝑆𝑁 = 𝑉𝐷𝐷 + 𝑣𝐷𝑆𝑃 ≈ 0
2 ]
𝑖𝐷𝑁 ≈ 𝑘𝑁 [2(𝑣𝐺𝑆𝑁 − 𝑉𝑡𝑁 )𝑣𝐷𝑆𝑁 − 𝑣𝐷𝑆𝑁
= 0 (𝑡𝑟í𝑜𝑑𝑜)
Figura 5 - Zona 5
8
Figura 6 - Característica de Transferência de vO(vI) prevista
RESUMO:
1ª Região de Funcionamento (NMOS cortado e PMOS tríodo)
A região encontra-se definida entre 0 ≤ 𝑣𝑖 ≤ 1.6𝑉:
2 ]
𝑖𝐷𝑃 ≈ 𝑘𝑃 [2(𝑣𝐺𝑆𝑃 + 𝑉𝑡𝑃 )𝑣𝐷𝑆𝑃 − 𝑣𝐷𝑆𝑃
= 0 (𝑡𝑟í𝑜𝑑𝑜)
Substituindo:
𝑖𝐷𝑃 ≈ 𝑘𝑃 [2(𝑉𝐷𝐷 − 𝑣𝑖 − |𝑉𝑡𝑃 |)(𝑉𝐷𝐷 − 𝑣0 ) − 𝑉𝐷𝐷 − 𝑣0 2 ] = 0
𝑣0 = 𝑉𝐷𝐷 = 13 𝑉
2ª Região de Funcionamento (NMOS saturado e PMOS tríodo)
Para 1.6 ≤ 𝑣𝑖 ≤ 5.8987 𝑉, temos que:
𝑘𝑁 (𝑣𝐼 − 𝑉𝑡𝑁 )2 = 𝑘𝑃 [2(𝑉𝐷𝐷 − 𝑣𝐼 − |𝑉𝑡𝑃 |)(𝑉𝐷𝐷 − 𝑣𝑂 ) − (𝑉𝐷𝐷 − 𝑣𝑂 )2 ]
Usando a ferramenta Solve do Mathematica, e resolvendo em ordem a 𝑣0 , obtém-se que
𝑣0 =7.6747 V
3ª Região de Funcionamento (NMOS saturado e PMOS saturado)
Igualamos as equações das correntes, obtendo a expressão:
𝑘𝑃 (𝑉𝐷𝐷 − 𝑣𝐼 − |𝑉𝑡𝑃 |)2 = 𝑘𝑁 (𝑣𝐼 − 𝑉𝑡𝑁 )2
Recorrendo novamente à ferramenta do Mathematica, mais especificamente à função Solve, e
substituindo pelos valores definidos.
9
𝑣𝑖 = 5.8987 𝑉
Nesta região o 𝑣0 encontra-se limitado, já que:

O transístor NMOS entra em tríodo quando 𝒗𝑶 < 𝒗𝒊 − 𝑽𝑻𝒐𝒏 ⇒ 𝒗𝟎 < 𝟒. 𝟐𝟗𝟖𝟕

O transístor PMOS sai do tríodo se 𝒗𝑶 > 𝒗𝒊 + |𝑽𝑻𝒑 | ⇒ 𝒗𝟎 > 𝟕. 𝟔𝟗𝟖𝟕
4ª Região de Funcionamento (NMOS tríodo e PMOS saturado)

As equações das correntes são igualadas, resultando na seguinte expressão:
𝑘𝑁 [2(𝑣𝐼 − 𝑉𝑡𝑁 )𝑣𝑂 − 𝑣𝑂2 ] = 𝑘𝑃 (𝑉𝐷𝐷 − 𝑣𝐼 − |𝑉𝑡𝑃 |)2

A região está definida em: 5.8987 < 𝑣𝑖 < 𝑉𝐷𝐷 − |𝑉𝑡𝑃 | = 11.2 𝑉

Para o limite inferior do intervalo, isto é, para 5.8987 V, 𝑣𝑂 = 4.2987, resolvendo a
equação das correntes
5ª Região de Funcionamento (NMOS tríodo e PMOS cortado)

A região está definida em: 𝑉𝐷𝐷 − |𝑉𝑡𝑃 | < 𝑣𝑖 < 𝑉𝐷𝐷 ⇒ 11.2<𝑣𝑖 <13 V

𝑘𝑁 [2(𝑣𝐼 − 𝑉𝑡𝑁 )𝑣𝑂 − 𝑣𝑂2 ] = 0, e desta forma 𝑣𝑂 = 0𝑉
𝐴
𝐴(1.6; 13)
𝑣𝑂 (𝑉)
𝐵(5.8987; 7.6987)
𝐶(5.8987; 4.2987)
𝐵
𝐷(11.2; 0)
𝐶
12
10
𝐷
8
𝑣𝑖 (𝑉)
6
4
2
2
4
6
8
10
12
Figura 7 –Característica de transferência obtida utilizando o programa Mathematica
10
Tal como podemos verificar, existe uma grande semelhança entre os gráficos da teórica e da
simulação. Assim, os valores obtidos através dos cálculos teóricos do Mathematica têm
correspondência com a literatura.
Pergunta II – 2
Para analisar a zona que funciona como amplificador (zona onde NMOS e PMOS estão em
saturação) recorre-se à análise incremental do circuito.
Tendo em conta que em DC o valor de VDD e VSS são nulos e que 𝜆 = 20𝑚𝑉 −1 e 𝑣𝐼 = 5.8987𝑉,
podemos obter o valor de 𝑣0 através da igualdade das equações das correntes no dreno, dada
por:
𝑘𝑃 (𝑉𝐷𝐷 − 𝑣𝐼 − |𝑉𝑡𝑃 |)2 (1 + 𝜆(𝑉𝐷𝐷 − 𝑣0 ) = 𝑘𝑁 (𝑣𝐼 − 𝑉𝑡𝑁 )2 (1 + 𝜆(𝑣0 )
Substituindo os valores obtém-se
𝑣0 = 6.5006𝑉
Para ser possível obter uma estimativa do ganho é necessário calcular as transcondutâncias e as
resistências de saída, r0n e r0p.
𝑟𝑜𝑁
𝑟𝑜𝑃
𝜕𝑖𝐷𝑁 −1
1
=|
= 3.7066 𝑘𝛺
| =
𝜕𝑣𝐷𝑆𝑃
𝜆[𝑘𝑁 (𝑣𝑖 − 𝑉𝑇𝑜𝑛 )2 ]
𝜕𝑖𝐷𝑃 −1
1
=|
= 3.7065 𝑘𝛺
| =
𝜕𝑣𝐷𝑆𝑃
𝜆[𝑘𝑃 (𝑉𝐷𝐷 − 𝑣𝑖 − |𝑉𝑇𝑝 |)2 ]
𝜕𝑖
𝑔𝑚𝑁 = |𝜕𝑣 𝐷𝑁 |
−1
𝐺𝑆𝑁
𝑔𝑚𝑃 = |
= 2𝑘𝑁 (𝑣𝑖 − 𝑉𝑇𝑜𝑛 ) = 6.2761 𝑚𝑆
𝜕𝑖𝐷𝑃 −1
| = 2𝑘𝑃 (𝑉𝐷𝐷 − 𝑣𝐼 − |𝑉𝑡𝑃 |) = 5.08925 𝑚𝑆
𝜕𝑣𝐺𝑆𝑃
O ganho é então dado por:
𝐴𝑣 =
𝑣0
= −(𝑔𝑚𝑃 + 𝑔𝑚𝑁 )(𝑟𝑜𝑃 //𝑟𝑜𝑁 )
𝑣𝑖
3.7065∗3.7066
𝐴𝑣 = −(5.08925 + 6.2761) (3.7065+3.7066) = −21.063𝑉/𝑉 = −26.5 dB
11
Pela análise da Figura 8 é possível constatar que para uma tensão de entrada de 13V o ganho é
de aproximadamente 20 V/V ou seja 26,021dB que é um valor ligeiramente inferior ao calculado.
Isto pode dever-se à variação de temperatura e realização de arredondamentos e aproximações
no cálculo do ganho.
Figura 8 - Variação do VDD em função do ganho
Pergunta II – 3
Neste ponto pretende-se obter uma estimativa das margens de ruído do inversor, em que a
margem de ruído é o ponto em que a derivada tem módulo maior que 1, isto é, quando a taxa
de variação local é elevada.
Desta forma, pretende-se encontrar dois pontos da característica de transferência que tenham
derivada unitária:
𝜕𝑣𝑜
= −1
𝜕𝑣𝑖
Figura 9 - Curva de Transferência com Margens de Ruído
12
Constata- se que estes pontos, visualizando o gráfico obtido, se encontram nas regiões B (NMOS
saturado e PMOS tríodo) e D (NMOS tríodo e PMOS saturado).

Região B:
𝑘𝑁 (𝑣𝐼 − 𝑉𝑡𝑁 )2 = 𝑘𝑃 [2(𝑉𝐷𝐷 − 𝑣𝐼 − |𝑉𝑡𝑃 |)(𝑉𝐷𝐷 − 𝑣𝑂 ) − (𝑉𝐷𝐷 − 𝑣𝑂 )2 ]
Utilizando o Mathematica, deriva-se esta equação em ordem a 𝑣𝐼 . Após isto, determina-se em
que ponto esta derivada assume o valor de -1, nesta região. Obtém-se que 𝑣𝑖 = 𝑉𝐼𝐻 = 4.5493
V.

Região D
𝑘𝑁 [2(𝑣𝐼 − 𝑉𝑡𝑁 )𝑣𝑂 − 𝑣𝑂2 ] = 𝑘𝑃 (𝑉𝐷𝐷 − 𝑣𝐼 − |𝑉𝑡𝑃 |)2
Deriva-se esta equação em ordem a 𝑣𝐼 . Após isto, determina-se em que ponto esta derivada
assume o valor de -1, nesta região. Obtém-se que 𝑣𝑖 = 𝑉𝐼𝐿 = 6.9391 V.
𝑉𝐼𝐻 = 4.5493𝑉
𝑉𝐼𝐿 = 6.9391𝑉
𝑁𝑀𝐻 = 𝑉𝑂𝐻 − 𝑉𝐼𝐻 = 𝑉𝐷𝐷 − 𝑉𝐼𝐻 = 8.4507𝑉 𝑁𝑀𝐿 = 𝑉𝐼𝐿 − 𝑉𝑂𝐿 = 𝑉𝐼𝐿 − 𝑉𝑆𝑆 = 6.9391𝑉
As margens de ruído não apresentam o mesmo valor devido ao facto de os transístores não
serem simétricos
13
III Trabalho de Simulação
Simulação em LT Spice
Ao longo desta secção é desenvolvida uma análise com recurso a um simulador, de maneira a
prever como os circuitos se irão comportar no laboratório em tempo real.
Para realizar o trabalho são nos fornecidos umas placas de montagem com os circuitos
integrados (onde estão incluídos os CMOS) já montados com alguns tipos de circuitos
preparados previamente no IST.
VDD
T2
vI
vO
T1
VSS
Figura 10 - Modelo simbólico do inversor lógico (à esquerda); Circuito integrado HEF 4007 (à direita)
Para poder simular o circuito em execução teve que ser inserido no programa LT Spice os dados
relativos aos MOSFET’s que serão utilizados, já que este não os incluía previamente, como seria
de esperar. Para isso, foram inseridos no endereço indicado de seguida:
“Endereco_definido_pelo_utilizador/LTSPICE4/lib/cmp/standard.mos”
As duas linhas de código seguintes:
Para o transístor NMOS:
.MODEL N4007 NMOS (TOX=70N KP=73u VTO=*V GAMMA=2.0 CBD=0.2p CBS=0.2p MJ=0.75
L=5u W=100u LAMBDA=20m)
Para o transístor PMOS:
.MODEL P4007 PMOS (TOX=70N KP=16u VTO=*V GAMMA=1.0 CBD=0.2p CBS=0.2p MJ=0.75
L=5u W=300u LAMBDA=20m)
14
Foi possível então construir o circuito planeado desta forma:
Com a saída em aberto
Figura 11 - Esquema em LTspice do circuito inversor lógico com Vo medido em circuito aberto (desprezando efeitos dos
cabos, osciloscópio, etc.)
Com a saída “Real”
Figura 12 - Esquema em LTspice do circuito inversor lógico, fazendo uma aproximação das impedâncias dos
instrumentos geradores/medida
Podemos agora responder às questões em concreto:
Pergunta III – 1
Vamos agora obter a curva de transferência Vo (Vi), sendo que a entrada (Vi) se trata da tensão
da porta dos dois transístores e a saída (Vo) corresponde ao dreno de ambos.
Para isso vamos efetuar um varrimento em tensão do circuito com Vi a variar de 0 a 13 V com
os seguintes parâmetros:
15
Figura 13 - Inputs inseridos pelo utilizador
para o modo de simulação DC sweep com
um varrimento em tensão de Vi a variar
desde 0 até 13 V de uma forma incremental
linear
Simulando o circuito aberto, obtemos o seguinte gráfico:
Figura 14 - Gráfico da característica de transferência Vo(Vi) para o circuito sem impedâncias externas, obtido através da simulação no
LTspice. A escala é de 1V por divisão do gráfico.
16
Tendo em conta agora a resistência e os dois condensadores (circuito “real”), obtemos este
gráfico:
Figura 15 - Gráfico da característica de transferência Vo(Vi) para o circuito com impedâncias externas, obtido através da simulação no LTspice. A escala é
de 1V por divisão do gráfico.
Como podemos ver não existem diferenças significativas.
Pergunta III – 2
Utilizando o comando referido no enunciado para a obtenção da derivada
𝑑𝑣𝑜
𝑑𝑣𝑖
:
Obteve-se o seguinte gráfico acima apresentado.
Figura 16 - Gráfico da característica de transferência Vo(Vi) juntamente com a derivada deste, obtido através da simulação no LTspice. A escala é de 1V por
divisão do gráfico.
17
Para a corrente iD(vi) foi possível traçar este gráfico:
Figura 17 - Gráfico da corrente elétrica dos drenos em função de Vi da montagem, obtido através da simulação no LTspice. A escala é de 1V por
divisão do gráfico.
A derivada vai nos dar um mínimo negativo, já que o circuito é um inversor: para sinais High, ele
vai responder com Low, e para sinais Low ele vai responder com High.
Logo, analisando o gráfico foi possível saber a localização deste mínimo no ponto de abcissa 5.85
V e de ordenada igual a -24.1071 V/V.
O módulo do ganho de tensão é máximo quando o valor de Vi = 5.85V e o seu ganho|𝐴𝑣| =
24.1071.
Vamos agora modificar a fonte de tensão Vin para fornecer ao circuito uma tensão igual a 5.85
V de maneira a obter o ponto de funcionamento em repouso para esta tensão. Para isso, foram
inseridos os seguintes dados:
Figura 18 - Inputs inseridos pelo utilizador para
o modo de simulação em ponto de
funcionamento em repouso
Foram então obtidos os seguintes resultados para o ponto de funcionamento em repouso:
18
VG = 5.85 V
VS2 = 13 V
VS1 = 0 V
VD1 = VD2 = 7.64662 V
ID1 = 0.0152021 mA
ID2 = 0.0152098 mA
VGS1 = 5.85 V
VSG2 = 7.15 V
VDS1 = 7.64662 V
VSD2 = 7.03833 V
Pergunta III – 3
Para resolver esta secção foram alterados os parâmetros gerais da simulação, e outros
específicos para o gerador, tendo sido modificados os seguintes campos:
Figura 19 - Inputs inseridos pelo utilizador para o modo de simulação em análise AC com um varrimento em
frequência a variar desde os 10 kHz até os 100 MHz, com um varrimento década a década e com cem pontos
19
Para o gerador Vi alterámos os seguintes parâmetros:
Figura 20 - Inputs inseridos pelo
utilizador para o gerador em
análise AC com uma função
sinusoidal com um offset DC de
5.85 V e 1 V de amplitude
Correndo a simulação, obteveos seguintes resultados para o
se
varrimento em frequência:
Figura 21 - Gráfico da tensão Vo em função de frequência da montagem, obtido através da simulação no LTspice. A escala é de 3 dB por divisão do
gráfico, vertical, e a horizontal em frequência variável por divisão.
20
Utilizando a ajuda de cursores conseguimos obter a frequência de corte a -3 dB de amplitude. O
valor de frequência obtido foi de f3 dB = 775.024 KHz
Figura 22 - Gráfico da tensão Vo em função de frequência da montagem, obtido através do LTspice. A escala é de 4
dB por divisão do gráfico, vertical, e a horizontal em frequência variável por divisão. São acrescentados cursores
para medir frequência de corte
Como podemos analisar pelo gráfico inicial, podemos facilmente deduzir que se trata de um
filtro do tipo “passa-baixo”, já que vai deixar passar as frequências baixas e atenuar as
frequências altas (a partir de 775.024 KHz começa a atenuar significativamente as altas
frequências, como podemos ver pela a análise do gráfico). Pela curva percebemos que existe
então um polo na frequência acima referida já que ela parece “descer” com um declive
aproximado de -20 dB por década. Vai ser o único polo da função e não vão haver zeros. A sua
função de transferência vai ter esta forma
𝐻(𝑠) =
𝑘
,
𝑠−775.024
com k real, e s em kHz
Passando agora o valor de 27.5291 dB para V/V: vai resultar em |𝐴𝑣| = 23.7933 V/V, muito
parecido ao obtido no exercício anterior de |𝐴𝑣| = 24.1071 V/V.
Comparando com os gráficos sem carga verificou-se que estes permaneciam inalterados e por
isso qualquer gráfico aqui inserido se tornava redundante.
21
Pergunta III – 4
Para proceder à simulação deste problema tivemos que alterar as características dos
condensadores de carga, de forma a podermos comparar com o catálogo do CMOS:
Figura 23 - Esquema em LTspice do circuito inversor lógico, fazendo uma aproximação das impedâncias dos instrumentos
geradores/medida, sendo que foi alterado o valor da impedância dos condensadores para 50 pF (estão em série e por
isso soma-se)
Utilizaram-se como parâmetros da
simulação e do gerador:
Figura 24 - Inputs inseridos pelo utilizador para o simulador em análise de transiente com um tempo de paragem de 3
períodos de onda (à direita) e para o gerador com uma função pulsada com os parâmetros indicados explicitamente (à
esquerda)
E
obtiveram-
22
se os gráficos seguintes para a tensão de entrada e de saída:
Figura 25 - Gráfico da tensão de saída Vo em função do tempo e da onda quadrada gerada pelo simulador em função do tempo. Uma
divisão vertical equivale a 1 V e uma horizontal equivale a 0.3 µs
Queremos agora obter o tempo de subida de Vo, para isso vamos fazer uma estimativa de 1090% de modo a encontrarmos o seu valor. Como 10 % de 13 V é igual a 1.3 V e 90 % equivale a
11.7 V, queremos obter o tempo que o sinal demora a “subir” desde os 1.3 V até aos 11.7 V.
Obtivemos assim o valor de 𝑡𝑟𝑖𝑠𝑒(10% − 90%) = 12.7489 ns, como é evidenciado na figura de
uma maneira aproximada.
Figura 26 - Gráfico da tensão de saída Vo em função do tempo e da onda quadrada gerada pelo
simulador em função do tempo. Uma divisão vertical equivale a 1 V e uma horizontal equivale a
3 ns. Medição do tempo de subida através de cursores
23
Para calcularmos o tempo de descida procedemos ao cálculo inverso, ou seja, o tempo que o
sinal demorou a descer de 11.7 V até 1.3 V, sendo que no final da análise vamos obter então o
valor do 𝑡𝑓𝑎𝑙𝑙(10% − 90%) = 7.87944 ns, aproximado, claro está.
Figura 27 - Gráfico da tensão de saída Vo em função do tempo e da onda quadrada gerada pelo simulador
em função do tempo. Uma divisão vertical equivale a 1 V e uma horizontal equivale a 0.002 µs. Medição
do tempo de descida através de cursores
Pelo facto do circuito não ser um inversor lógico ideal, ele vai introduzir períodos de redundância
nos quais ele interpreta com High e outros em que ele interpreta como Low, sendo estes os
atrasos produzidos pelo sistema. Podem então ser medidos dois tempos de atraso: tdLH e tdHL.
tdLH corresponde ao tempo de atraso que o sinal de saída demora a passar de Low para High
enquanto o de saída se encaminha para Low vindo de High(ou seja, a passar de 0 para 6.5 V para
o sinal de saída, e a passar de 13 para 6.5 V para o sinal de entrada respetivamente).
24
Figura 28 - Gráfico da tensão de saída Vo em função do tempo e da onda quadrada gerada pelo simulador em
função do tempo. Uma divisão vertical equivale a 1 V e uma horizontal equivale a 0.6 ns. Medição do tdLH através
de cursores
Obteve-se assim o seguinte valor de tdLH = 4.99892 ns.
De forma inversa para calcular o tempo de atraso tdHL, procedeu-se da seguinte forma: medimos
então o tempo entre o instante em que o sinal de entrada atinge 50% do seu valor (High – Low)
enquanto este se encontra a subir e o instante em que o sinal de saída atinge 50% do seu valor
(High – Low) enquanto desce. Procedendo desta forma, obteve-se tdHL = 3.31808 𝑛𝑠.
Figura 27 - Gráfico da tensão de saída Vo em função do tempo e da onda quadrada gerada pelo simulador em
função do tempo. Uma divisão vertical equivale a 1 V e uma horizontal equivale a 0.001 µs. Medição do tdHL
através de cursores
25
Comparando agora com as características do fabricante:
Resumindo tudo numa tabela:
Simulacão
Catálogo
𝑡𝑟𝑖𝑠𝑒(10%−90%)
12.7489ns
20<x<30
𝑡𝑓𝑎𝑙𝑙(10%−90%)
7.87944 ns
20<x<30
tdLH
4.99892 ns
15<x<20
tdHL
3.31808 ns
15<x<20
26
IV Trabalho Experimental
Efectuaram-se algumas medições a partir da montagem do inversor CMOS usando a base de
montagem TEE 03 que contém um circuito integrado HEF4007 e duas resistências R1= 22kΩ e
R2=100kΩ com um ponto médio comum. Utilizam-se os transístores T1 (NMOS) e T2 (PMOS) que
já têm os substratos ligados às fontes. A tensão VDD utilizada foi de 13V.
Figura 28 - Base de montagem TEE 03
Para realização deste trabalho experimental utilizaram-se um gerador DC Topward 6303D, um
gerador de sinais Centrad GF 467F, um osciloscópio Agilent Technologies DSO-X 2024A 200MHz
(2GSa/s) e um multímetro Kiotto KT1993HZ. Para comparação com valores tabelados recorreuse ao catálogo da Philips: “HEF4007UB gates Dual complementary pair and inverter”.
Pergunta IV – 1 – Análise das tensões de entrada e de saída; característica vO(vI)
Figura 29 - Representação das tensões de entrada vI (a laranja) e de saída vO (a verde) no osciloscópio
27
O gerador vI é um gerador de funções. Produziu-se um sinal sinusoidal de cerca de 100Hz. Como
tem uma alimentação DC assimétrica, VSS=0, ajustou-se a tensão de desvio (offset) do gerador
para VDD/2 e a amplitude máxima deve ser igual a VDD/2=13/2=6.5V, isto é, vI varia de 0 a VDD.
Tal como podemos verificar (apesar das aproximações) na figura, em que cada quadrícula
equivale a 2.00V, em ambos os sinais.
Através da análise do gráfico, podemos constatar o correcto funcionamento do inversor CMOS.
Uma vez que partimos de um sinal de entrada vI de amplitude máxima (13V), a que corresponde
um vO mínimo (0V) (e vive-versa). Ambos os sinais encontram-se em oposição de fase.
O gerador de funções não consegue emitir um sinal de 13V, daí que vI não atinja o seu máximo
(há distorção), contudo em vO denota-se com facilidade a zona de saturação.
Figura 30 - Característica vO(vI) usando o osciloscópio no modo XY
A entrada do osciloscópio relativa a vI é aplicada na deflexão horizontal (eixo dos xx) onde
normalmente é aplicado o sinal de base de tempo (trigger); e a entrada do osciloscópio relativa
a vO é aplicada na deflexão vertical (eixo dos yy).
Quando vI tem valores muito baixos, vO tem o seu máximo e vice-versa: quando vI atinge os
valores mais elevados, vO tem o seu mínimo.
O gráfico obtido aproximada-se do das teóricas e da simulação. Na zona de saturação há um
declive muito acentuado.
28
Pergunta IV – 2 – Análise dos tempos de subida, descida e de atraso de propagação
do inversor
Nesta alínea mudou-se a onda sinusoidal para quadrada e ajustou-se a frequência do gerador
de sinais (ligado directamente ao osciloscópio) para 1MHz (período de sinal 1µs). Após ligar o
gerador ao inversor CMOS ajustou-se o nível dos impulsos a serem iguais às tensões de
alimentação DC (vIH=VDD e vIL=VSS).
Figura 31 - Visualização da onda quadrada vI (laranja) e vO (verde), com respectivos tempos de subida e descida
Verificou-se que os tempos de subida e descida são rápidos (da ordem dos ns), contudo os
valores são superiores aos previstos (típicos). São também inferiores ao máximo, ou seja estão
dentro do intervalo expectável. Não esquecendo que não existe uma tabela para VDD = 13V,
apenas nos podemos guiar por 5 e 10V.
Figura 32 - Valores para os tempos de subida, descida e de transição (tabela da página 3 do catálogo)
29
De forma a calcular os tempos de atraso de propagação do inversor aumentou-se a escala de
tempo do osciloscópio e utilizou-se a opção Retard.
Figura 33 - Tempo de atraso de propagação do inversor (high-low): quando vI aumenta e vO diminui
Figura 34 - Tempo de atraso de propagação do inversor (low-high): quando vI diminui e vO aumenta
Estes valores encontram-se no limite máximo dos tabelados.
30
Figura 35 - Tabela com o registo dos tempos de subida, descida e de atraso do inversor para os sinais de entrada e
saída
O tempo de descida é sempre superior ao de subida, uma vez que os condensadores demoram
mais tempo a descarregar do que a carregar (maior 𝜏, mais lento).
O tempo de atraso low-high é superior ao high-low.
Tal como se verificou no primeiro trabalho laboratorial, não existem ondas quadradas perfeitas,
o gerador de sinais simplesmente não as consegue gerar. Por essa razão, os tempos de
comutação são obtidos, subtraindo os tempos de subida e descida do sinal de saída pelos do
sinal de entrada, respectivamente. Assim sendo, o tempo de subida foi de 50 ns, enquanto o de
descida foi de 25 ns.
Ao se comparar com os valores do catálogo pode-se concluir que apresentam algumas
diferenças graças à distorção apresentada no osciloscópio, relativa ao sinal de entrada, e à carga
capacitiva associada ao cabo coaxial.
31
Pergunta IV – 3 (facultativa) – Dispersão de Fabrico
VDD
VDD
R
T2
vO
vO
R
T1
Figura 36 - Montagem dos TECMOS na zona de saturação para obter os parâmetros K e Vt
Ambos os transístores operam na zona de saturação: 𝑣𝐺𝐷 = 0
Corrente de dreno: |𝑖𝐷 | = 𝐾(|𝑣𝐺𝑆 | − |𝑉𝑡 |)2
Transístor NMOS T1
Análise para a resistência 𝑹𝟏 :
𝑣𝐺𝑆1 = 1.775𝑉
𝑅1 = 101.200𝑘Ω
Através da lei de Ohm: 𝑖𝐺𝑆 =
𝑣𝐺𝑆
𝑅
= 𝑖𝐷 (no caso de T1)
𝑖𝐷1 =
𝑣𝐺𝑆1
1.775𝑉
=
= 17.540𝜇𝐴
𝑅1
101.200𝑘Ω
Análise para a resistência 𝑹𝟐 :
𝑣𝐺𝑆2 = 4.570𝑉
𝑅2 = 2.162𝑘Ω
𝑖𝐷2 =
𝑣𝐺𝑆2
4.570𝑉
=
= 2.114𝑚𝐴
𝑅2
2.162𝑘Ω
Resolução de um sistema de duas equações a duas incógnitas, para determinar os valores de K
e Vt.
17.540 ∗ 10−6 = 𝐾𝑁 (1.775 − |𝑉𝑡𝑁 |)2 ⇒ 𝐾𝑁 =
2.114 ∗ 10
−3
= 𝐾𝑁 (4.570 − |𝑉𝑡𝑁 |)2 ⇒ 𝐾𝑁 =
17.540 ∗ 10−6
(1.775 − |𝑉𝑡𝑁 |)2
2.114 ∗ 10−3
(4.570 − |𝑉𝑡𝑁 |)2
Através do programa Wolfram Mathematica, ao igualar K:
17.540 ∗ 10−6
2.114 ∗ 10−3
𝑖𝐷1
𝑖𝐷2
=
⇔
=
(1.775 − |𝑉𝑡𝑁 |)2 (4.570 − |𝑉𝑡𝑁 |)2
(𝑣𝐺𝑆1 − |𝑉𝑡𝑁 |)2 (𝑣𝐺𝑆2 − |𝑉𝑡𝑁 |)2
Obteve-se para Vt duas hipóteses de solução (em V):
{V𝑡𝑁 → 2.00834}, {V𝑡𝑁 → 1.49489}
Os valores apresentados para o Vt do NMOS são positivos e para o PMOS negativos.
32
Para V𝑡𝑁 = 2.00834𝑉 ⇒ 𝐾𝑁 = 2.23549 ∗ 10−4 𝐴𝑉 −2
Para V𝑡𝑁 = 1.49489 ⇒ 𝐾𝑁 = 3.22145 ∗ 10−4 𝐴𝑉 −2
Transístor PMOS T2
Análise para a resistência 𝑹𝟏 :
𝑣𝐺𝑆1 = 2.065𝑉
𝑅1 = 101.200𝑘Ω
𝑖𝐷1 =
𝑣𝐺1
15.065𝑉
=
= 14.886𝜇𝐴
𝑅1
101.200𝑘Ω
𝑣𝐺𝑆 = 𝑣𝐺 − 𝑣𝑆 ⇔ 𝑣𝐺 = 𝑣𝐺𝑆 + 𝑣𝑆 ⇒ 𝑣𝐺1 = 2.065 + 13 = 15.065𝑉
𝑣𝑆 = 𝑉𝐷𝐷 = 13𝑉
Análise para a resistência 𝑹𝟐 :
𝑣𝐺𝑆2 = 5.010𝑉
𝑅2 = 2.162𝑘Ω
𝑖𝐷2 =
𝑣𝐺2 18.010𝑉
=
= 8.330𝑚𝐴
𝑅2
2.162𝑘Ω
𝑣𝐺 = 𝑣𝐺𝑆 + 𝑣𝑆 ⇒ 𝑣𝐺2 = 5.010 + 13 = 18.010𝑉
Resolução de um sistema de duas equações a duas incógnitas, para determinar os valores de K
e Vt.
14.886 ∗ 10−6 = 𝐾𝑃 (2.065 − |𝑉𝑡𝑃 |)2 ⇒ 𝐾𝑃 =
14.886 ∗ 10−6
(2.065 − |𝑉𝑡𝑃 |)2
8.330 ∗ 10−3 = 𝐾𝑃 (5.010 − |𝑉𝑡𝑃 |)2 ⇒ 𝐾𝑃 =
8.330 ∗ 10−3
(5.010 − |𝑉𝑡𝑃 |)2
Através do programa Wolfram Mathematica, ao igualar K:
14.886 ∗ 10−6
8.330 ∗ 10−3
𝑖𝐷1
𝑖𝐷2
=
⇔
=
2
2
2
(2.065 − |𝑉𝑡𝑃 |)
(5.010 − |𝑉𝑡𝑃 |)
(𝑣𝐺𝑆1 − |𝑉𝑡𝑃 |)
(𝑣𝐺𝑆2 − |𝑉𝑡𝑃 |)2
Obteve-se para Vt duas hipóteses de solução (em V):
{V𝑡𝑃 → −2.18445}, {V𝑡𝑃 → −1.93501}
Para V𝑡𝑃 = −2.18445𝑉 ⇒ 𝐾𝑃 = 1.04329 ∗ 10−3 𝐴𝑉 −2
Para V𝑡𝑃 = −1.93501𝑉 ⇒ 𝐾𝑃 = 8.80964 ∗ 10−4 𝐴𝑉 −2
33
Valores catalogados
Cálculo do VtN e VtP
No catálogo da Philips, não existem directamente os valores de K e Vt. Através dos gráficos 3 a
5 e 7 do catálogo, consegue-se obter uma estimativa do Vt.
Através da observação do gráfico 5 do catálogo consegue-se determinar Vtn. Sabe-se que para
existir corrente iD (iD > 0A), isto é, na ZONA 2 [NMOS saturado (ON) e PMOS em tríodo (ON)]
tem-se:
𝒗𝑰 = 𝒗𝑮𝑺𝑵 ≥ 𝑽𝒕𝑵
E neste caso, através do gráfico podemos verificar que quando vI ≥ 2V, iD começa a aumentar,
logo:
𝑽𝒕𝑵 = 𝟐𝑽
Figura 37 - Corrente de dreno ID e tensão de saída VO como função da tensão de entrada VI; VDD = 15V; Tamb = 25ºC
(figura 5 do catálogo)
Desta forma, pode-se concluir que o primeiro valor achado para VtN será o mais correcto (V𝑡𝑛 →
2.00834𝑉).
Aplicando este raciocínio ao transístor PMOS, tem-se:
𝑣𝐼 = 𝑣𝐺𝑃
𝑣𝑆𝑃 = 𝑉𝐷𝐷 = 15𝑉 (pela legenda do gráfico)
𝑣𝐺𝑆𝑃 = 𝑣𝐼 − 𝑉𝐷𝐷 ⇒ 𝑣𝐺𝑆𝑃 = 𝑣𝐼 − 𝑉𝐷𝐷 ≤ 𝑉𝑡𝑃
𝒗𝑰 ≤ 𝑽𝒕𝑷 + 𝑽𝑫𝑫
Através da análise do gráfico consegue-se concluir que começa a existir corrente iD quando 𝑣𝐼 ≤
14 𝑉. Ou seja, temos no limite superior 𝑣𝐼 = 14 𝑉:
𝑉𝑡𝑃 + 𝑉𝐷𝐷 = 14 ⇒ 𝑉𝑡𝑃 = 14 − 15 = −1𝑉
Confirma-se assim que os valores para o VtP são negativos:
𝑽𝒕𝑷 = −𝟏𝑽
34
Cálculo do KN e KP
Relativamente ao cálculo do K, sabendo que a transcondutância em AC é dada no PFR (Ponto de
Funcionamento em Repouso) por: 𝑔𝑚 =
𝒈𝒎 𝟐
)
𝟐
Tem-se: 𝑲 = (
𝑑𝑖𝐷
𝑑𝑣𝐺𝑆
= 2√𝐾𝐼𝐷
𝟏
×𝑰
𝑫
Da curva A (A de average, valores médios) da Figura 10 do catálogo tira-se o valor de gfs para um
dado VDD. O significado de gfs é a transcondutância directa (f de forward) com o inversor em
curto-circuito em AC (s de short-circuit).
Figura 38 - Transcondutância directa gfs como função de VDD a uma Tamb = 25ºC (figura 10 do catálogo)
Pelo gráfico da figura 3 pode-se concluir que, para a curva A, quando VDD = 13V tem-se:
𝑔𝑓𝑠 = 7.25 𝑚𝐴𝑉 −1 = 7.25 ∗ 10−3 𝐴𝑉 −1
Da curva da figura 4 obtém-se o correspondente ID ou IDD como é denominado no catálogo.
Figura 39 - Corrente IDD como função da tensão VDD (figura 7 do catálogo)
35
Para VDD = 13V, temos:
𝐼𝐷𝐷 = 12.5 𝑚𝐴 = 12.5 ∗ 10−3 𝐴
O circuito de teste usado para calcular gfs está representado na figura 5. Note-se que, ao colocar
um amperímetro na saída se está a introduzir um curto-circuito na saída em AC (condensador
de 100µF a bloquear a corrente DC). Deste modo, toda a corrente dos geradores comandados
que estão entre o dreno e as fontes dos modelos do NMOS e do PMOS, 2gmvgs (admitindo que
têm o mesmo gm), vai para o amperímetro, não influenciando a medida as resistências ro dos
modelos dos dois transístores.
Figura 40 - Circuito eléctrico para medição da transcondutância directa gfs a uma tensão vO constante
Desta forma temos:
𝑔𝑚 =
𝑔𝑓𝑠 7.25 ∗ 10−3
=
= 3.625 ∗ 10−3 𝐴𝑉 −1
2
2
Note-se que em AC, regime dinâmico, os transístores estão em paralelo, logo as correntes
somam-se e os gm também.
𝑔𝑚𝑝 = 𝑔𝑚𝑛
2
𝑔𝑓𝑠 2 1
7.25 ∗ 10−3
1
𝐾𝑛 = 𝐾𝑝 = ( ) × = (
= 2.628125 × 10−4 𝐴𝑉 −2
) ×
4
𝐼𝐷
4
12.5 ∗ 10−3
Este valor é comparável ao primeiro Kn obtido (à semelhança do valor de VtN que se obteve
anteriormente, que também era comparável à primeira hipótese).
Quadro de comparações
De seguida, compara-se os valores experimentais obtidos para os K e Vt dos transístores com os
usados no modelo do LTSpice. Note-se que a constante K = 2 KX W/L, com X = N ou P consoante
se trata do NMOS ou do PMOS. Quanto a Vt é denominado no modelo LTspice por VTO.
Valores experimentais
VtN (V)
VtP (V)
KN (AV-2)
KP (AV-2)
2.00834
−2.18445
2.23549 ∗ 10−4
10.04329 ∗ 10−4
1.49489
−1.93501
3.22145 ∗ 10−4 𝐴𝑉 −2
8.80964 ∗ 10−4
Valores
catalogados
2
−1
2.628125 ∗ 10−4
2.628125 ∗ 10−4
Valores do
LTSpice
1.6
−1.8
0.73 ∗ 10−4
0.16 ∗ 10−4
36
Desta forma, pode-se concluir que se obtiveram valores da mesma ordem de grandeza a nível
de valores medidos e teóricos (tanto da simulação e do catálogo). Isto é, na ordem dos volts (V)
para Vt e 10-4 para K. Contudo, denotam-se algumas diferenças, pelo que não se obtiveram
exactamente os mesmos valores.
A diferença de valores registados no catálogo podem ser explicados pelo facto de neste surgir
VDD=15V e não VDD=13V, como no nosso caso. Além de que, as características descritas no
modelo do catálogo podem não corresponder na perfeição aos transístores utilizados na prática
(até porque há que considerar o desgaste das componentes) Assim, compreende-se o porquê
dos valores de Vt experimentais e da simulação serem mais semelhantes entre si. Não
esquecendo os erros de medição, nomeadamente com o multímetro para obter Vt e K.
As soluções para o KP fornecidas pelo programa Mathematica distanciaram-se dos valores
catalogados, possivelmente não se deve ter em conta estas medidas.
Nestas imagens pode-se visualizar a montagem dos circuitos realizadas durante a actividade
experimental. Isoladamente analisou-se cada transístor em separado:
Figura 41 - Circuito relativo ao transístor T2 (PMOS)
Figura 42 - Circuito relativo ao transístor T1 (NMOS)
Conclusões
Através desta actividade experimental consolidaram-se os conhecimentos sobre transístores
MOS, efectuando sempre o paralelismo com os transístores TJB. A utilização do circuito inversor
CMOS permitiu estudar ao detalhe o funcionamento de NMOS (T1) e PMOS (T2).
37
Constatou-se o objectivo de um inversor CMOS, isto é, a inversão do sinal de entrada. Sabe-se
também que este inversor CMOS é muito utilizado em circuitos lógicos, onde a tensão de saída
toma apenas os valores lógicos 0 ou 1 (porque se aproxima de uma onda quadrada perfeita).
Como os transístores na prática não têm uma camada de óxido isolante perfeita, quando se
encontram nas zonas de corte a corrente iG não é exatamente nula, o que conduz a discrepâncias
nos valores medidos ao longo da actividade. Além de que também se desprezou o factor 𝜆.
Relativamente à curva de transferência vO(vI), considerou-se que o comprimento do canal n era
constante, daí que iD fosse independente de vDS, a partir do momento em que o transístor entra
na região de saturação (ZONA 3 – BC, a intermédia). Apesar da na teoria se prever uma recta de
declive infinito, na prática não acontece, visto que teria um ganho de tensão infinito (mas existe
ganho à mesma). Ou seja, obteve-se uma região estreita com a respectiva mancha de ruído. As
curvas de transferência obtidas das perspectivas teórica, computacional e experimental são
semelhantes entre si, contudo há que ter em conta que na parte experimental, na zona de
saturação, a curva de transferência não adquire uma inclinação recta, havendo também
fenómenos de distorção.
Relativamente ao cálculo das transcondutâncias, além de se efectuar uma interpolação no
gráfico da figura 40 para o cálculo do gfs de VDD=13V, efetuaram-se aproximações. No
desenvolvimento do polinómio de Taylor, desprezaram-se os termos de ordem superior, por se
considerarem infinitesimais em comparação com o primeiro termo.
O ganho teórico, comparando o teórico, que foi de 26.5 dB, com o simulado, de 27.64 dB,
verifica-se uma viável proximidade entre os valores obtidos.
As margens de ruído obtidas teoricamente foram de 8.4507 e 6.9391 V para NMH e NML,
respectivamente. Experimentalmente, não se obtiveram estas margens de ruído contudo
podemos inferir que as tensões correspondentes a estas margens encontram-se nas regiões 4 a
6 V, e de 6 a 8V, observando a curva de transferência (derivada igual a -1). Já na simulação, podese visualizar os pontos onde a derivada era -1, sendo esses pontos correspondentes a tensões
de 4.31695 V e 7.04752 V. Desta forma, temos que NMH vai ser de 8.68305 e NML7.04752.
Pode-se então ver que os resultados teóricos e os resultados da simulação são aproximados.
Em relação aos tempos de comutação, na parte computacional obtiveram-se 7.87944 ns para o
tempo de subida, enquanto o tempo de descida foi de 12.7489 ns. Na simulação, os valores
adquiridos foram bastante diferentes, sendo bastante maiores. Isto pode-se dever ao facto de
o gerador ser incapaz de gerar sinais ideais. Experimentalmente, os tempos de comutação são
obtidos, subtraindo os tempos de subida e descida do sinal de saída pelos do sinal de entrada,
respectivamente. Assim sendo, o tempo de subida foi de 50 ns, enquanto o de descida foi de 25
ns. Comparando com o catálogo, este não indica os valores dos tempos de subida e descida para
13 V. Por isso, utilizam-se as equações apresentadas no catálogo. Substituindo CL por 111pF
(devido aos condensadores de 11 e 100pF se encontrarem em paralelo), calcula-se depois a
diferença dos tempos de subida e descida entre 10 e 15 V, multiplica-se esta diferença por 60%
(correspondente aos 13 V), a qual se subtrai ao tempo de 10 V. Os tempos de subida e descida
são iguais, e equivalem a 44.38 ns. Assim, pode-se concluir que os valores experimentais se
aproximam mais dos valores catalogados, à excepção de tempo de descida
38
Os tempos de propagação obtidos na simulação foram para tdHL 3.318 ns e para tdLH 4.999 ns,
que comparando com os valores experimentais, que foram de 40 e 46.9 ns, pode-se constatar
que são valores muito díspares.
Este trabalho experimental permitiu verificar que se conseguem obter valores da mesma ordem
de grandeza (apesar de alguma diferenças), através do programa Mathematica com cálculos
teóricos, do programa LTSpice para simulação e da medição experimental. Por vezes não se
obtiveram resultantes semelhantes entre estas três formas de obter valores devido ao catálogo
da Philips (só tinha VDD=15V e não 13V) não ser específico para o nosso caso, erros experimentais
executados na prática ou até mesmo o efeito dos cabos coaxiais (e também dos restantes
aparelhos). Por outro lado, verificou-se que as aproximações da análise teórica (esquema
incremental equivalente em que se tem em conta o valor de ro ou mesmo desprezar o
osciloscópio) são válidas pois são concordantes com os resultados reais.
Bibliografia
[1] Electrónica Geral – Trabalho de Laboratório 0; FREIRE, João Costa; Fevereiro de 2014
[2] Electrónica Geral – Transparências de apoio às aulas; FREIRE, João Costa; Fevereiro de 2014
[3] Circuitos com Transístores Bipolares e MOS; SILVA, Manuel de Medeiros; Fundação Calouste
Gulbenkian
39
[4] Microelectronic Circuits; SEDRA, Adel S.; SMITH, Kenneth C.; Fifth Edition; Oxford University
Press
40