MOVIMENTOS BI E TRIDIMENSIONAL

Movimentos bi e tridimensional
35
MOVIMENTOS
BI E
TRIDIMENSIONAL
3
3.1 Introdução
O movimento unidimensional que vimos no capítulo anterior é um
caso particular de uma classe mais ampla de movimentos que ocorrem em
duas ou três dimensões. Se o movimento de um corpo está completamente
restrito a um plano, ele é denominado movimento plano ou bidimensional.
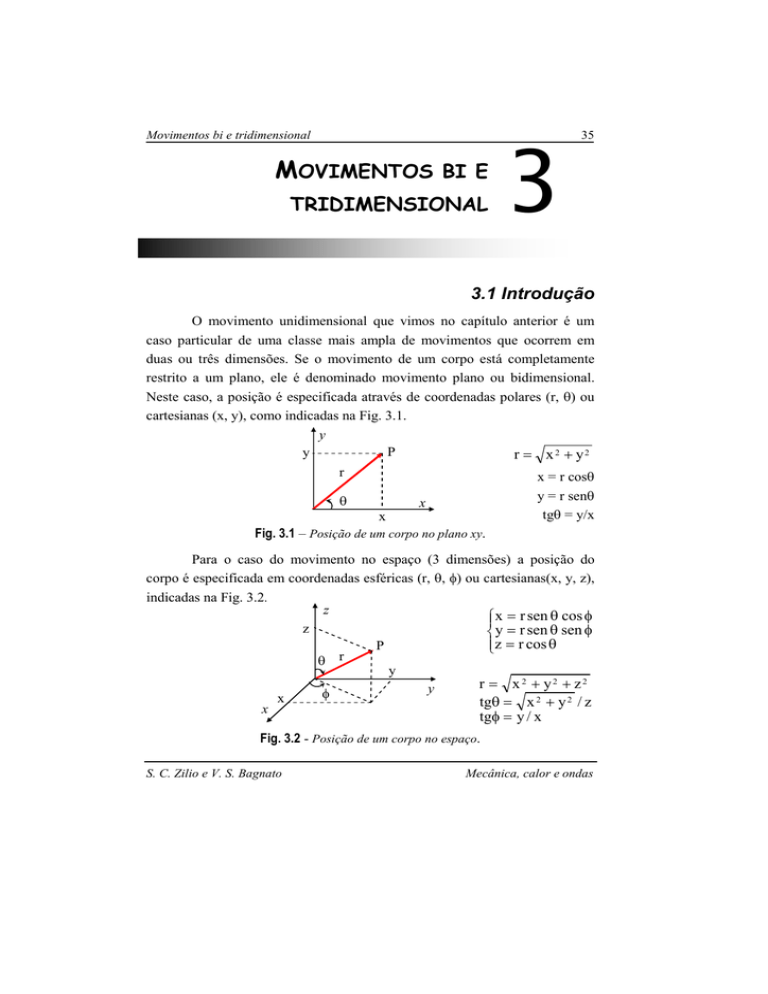
Neste caso, a posição é especificada através de coordenadas polares (r, θ) ou
cartesianas (x, y), como indicadas na Fig. 3.1.
y
P
y
r = x 2 + y2
r
θ
x = r cosθ
y = r senθ
tgθ = y/x
x
x
Fig. 3.1 – Posição de um corpo no plano xy.
Para o caso do movimento no espaço (3 dimensões) a posição do
corpo é especificada em coordenadas esféricas (r, θ, φ) ou cartesianas(x, y, z),
indicadas na Fig. 3.2.
z
x = r sen θ cos φ
z
 y = r sen θ sen φ
z = r cos θ
P
θ r
y
r = x 2 + y2 + z2
y
φ
x
tgθ = x 2 + y 2 / z
x
tgφ = y / x
Fig. 3.2 - Posição de um corpo no espaço.
S. C. Zilio e V. S. Bagnato
Mecânica, calor e ondas
Movimentos bi e tridimensional
36
Para movimentos planos e espaciais, as grandezas cinemáticas
r r r
( r , v e a ) não são necessariamente paralelas como acontece no movimento
unidimensional. Desta forma, é de importância fundamental tratar estas
grandezas vetorialmente.
r
Se no tempo t1 a posição do corpo for descrita pelo vetor posição r1 e
r
no tempo t2, pelo vetor posição r2 , podemos dizer que o deslocamento sofrido
r r r
r
pelo corpo é dado por ∆ r = r2 − r1 onde ∆ r não é necessariamente a
r
distância percorrida pelo corpo. Havendo um deslocamento ∆ r num intervalo
r
de tempo ∆t = t2 – t1, podemos definir as velocidades média (v m ) e instantânea
(vr ) da forma:
r
r
∆r
vm =
∆t
r
r
r
∆r dr
v = lim ∆t →0
=
∆t dt
Vemos que a velocidade sempre existirá quando houver mudanças no
módulo e/ou direção do vetor posição. A variação temporal de um vetor pode
ser analisada através da variação temporal de suas componentes, da forma:
r
r dx
dy
dz
r = x î + y î + z k̂ ⇒ v =
î +
ĵ + k̂
dt
dt
dt
e isto pode ser feito porque os versores î , ĵ e k̂ não variam com o tempo.
Exemplo: Vamos determinar a velocidade de um corpo cujo vetor
r
posição é dado por: r = 4 t 2 î + 3t ĵ . Tomando-se as derivadas temporais das
r
componentes de r temos:
r
r
v = d r / dt = 8t î + 3 ĵ
Vamos usar este exemplo para demonstrar uma relação importante. Podemos
escrever:
S. C. Zilio e V. S. Bagnato
Física Básica – Mecânica, calor e ondas
Movimentos bi e tridimensional
37
r
2
2
r ( t + ∆t ) = 4( t + ∆t ) î + 3( t + ∆t ) ĵ = 4 t 2 î + 3t ĵ + 8t∆t î + 3∆t ĵ + 4(∆t ) î
No caso em que ∆t é muito pequeno, (∆t)2 << ∆t e o termo (∆t)2 pode
ser desprezado. Assim,
r
r
r r
r
r (t + ∆t ) = r (t ) + ∆ r = r (t ) + v ∆t
e dizemos que esta é uma aproximação de primeira ordem em ∆t, já que o
termo (∆t)2 foi desprezado. A aceleração do corpo é definida como:
r
r
r
∆v dv
a = lim ∆t →0
=
∆t dt
e, portanto, sempre haverá aceleração quando houver mudanças do vetor
velocidade, seja em módulo, direção ou sentido.
r
Exemplo: A velocidade de um corpo é dada por v(t ) = 3t 2 î + t ĵ + t 3 k̂ .
r
Logo, a aceleração é dada por a (t ) = 6 t î + ĵ + 3t 2 k̂
3.2 Decomposição de movimentos
r dx
dy
dz
Do fato que v =
î +
ĵ + k̂ tiramos que v x = dx/dt , vy =
dt
dt
dt
dy/dt e v z = dz/dt , de modo que se olharmos para cada componente, o
movimento do corpo pode ser analisado independentemente, ou seja, a
velocidade na direção x só depende da variação da coordenada x com o tempo,
etc. Este resultado pode ser generalizado e o movimento espacial de um corpo
pode ser tratado independentemente em cada uma das três direções.
Resumindo, temos o chamado princípio da independência dos movimentos ou
princípio de Galileu:
“Quando um corpo se encontra sob a ação simultânea de dois ou mais
movimentos, cada um se processa como se os demais não existissem”.
Em outras palavras, a posição do móvel depois de um intervalo de
tempo sob a ação do movimento composto é a mesma que resultaria se o
móvel se deslocasse por etapas em cada direção. Como um exemplo típico,
S. C. Zilio e V. S. Bagnato
Mecânica, calor e ondas
Movimentos bi e tridimensional
38
consideremos o caso de um barco com velocidade vb atravessando um rio cuja
correnteza tem velocidade vr. O barco percorrerá uma trajetória que consiste
em deslocar-se vrt na direção do rio e vbt na direção perpendicular, como
r
mostra a Fig. 3.3. Assim, r = v r t î + v b t ĵ
e
v = v r î + v b ĵ .
ĵ
vr
vb t
î
vr t
Fig. 3.3 - Movimento de um barco num rio com correnteza.
3.3 Movimento acelerado
Podemos generalizar o que vimos para o movimento unidimensional
escrevendo:
t r
r r
r = r0 + ∫ v( t ) dt
0
t r
r
r
v( t ) = v 0 + ∫ a ( t ) dt
0
A integração de vetores pode ser executada componente a
componente, como no caso da derivação. Portanto,
t
rz = rz0 + ∫ v z ( t ) dt
0
e assim por diante. No caso da aceleração ser constante temos:
r
r r r
r r
1r
v = v 0 + at e r = r0 + v 0 t + a t 2
2
S. C. Zilio e V. S. Bagnato
Física Básica – Mecânica, calor e ondas
Movimentos bi e tridimensional
39
Podemos analisar este movimento através do sistema de equações:
Para a velocidade:
Para a posição:
v x = v 0x + a x t
rx = rx0 + v 0x t + 12 a x t 2
v y = v 0y + a y t
ry = ryo + v 0y t + 12 a y t 2
v z = v 0z + a z t
rz = rz0 + v 0z t + 12 a z t 2
Vamos em seguida ver alguns exemplos de movimento acelerado.
a) Lançamento de projétil
Um caso importante de movimento plano é aquele onde temos:
r
a = −g ĵ (com g = 9.8 m/s2) que corresponde ao movimento de um corpo
atirado de maneira arbitrária. Neste caso, o movimento será acelerado na
direção y e não acelerado nas demais. Vamos imaginar a situação em que o
corpo é lançado obliquamente de maneira a formar um ângulo θ com a
superfície, como mostrado na Fig. 3.4
y
v 0x = v 0 cos θ
v 0y = v 0 sen θ
v0
θ
x
Fig. 3.4 – Lançamento oblíquo de um projétil.
Tomando-se o eixo x paralelo à superfície e o eixo y na vertical, a
e
velocidade inicial v0 pode ser decomposta em v 0x = v 0 cos θ
o
v y = v 0 sen θ . Na direção x não existe aceleração, porém na direção y
temos ay = -g de modo que:
v x (t ) = v 0x = v 0 cos θ

0
x (t ) = x 0 + v x t = x 0 + v 0 cos θ t
S. C. Zilio e V. S. Bagnato
Mecânica, calor e ondas
Movimentos bi e tridimensional
40
v y ( t ) = v 0y − g t = v o sen θ − g t

 y(t ) = y 0 + v 0y t − 12 g t 2
Eliminando-se o tempo do primeiro conjunto de equações
(t = (x − x 0 ) / v 0x ) e substituindo no segundo obtemos:
y = y0 + v
0
y
(x − x 0 )
v 0x
 x − x0 
− g

2  v 0x 
2
1
que representa uma trajetória parabólica como indicada na Fig. 3.5. A altura
máxima pode ser calculada tomando-se dy/dx = 0. Assim,
v 0y
v 0x
−g
(x − x 0 )
v 0x
2
= 0 ⇒ x max = x 0 +
v 0y v 0x
g
e substituindo em y(t) tiramos:
y max = y 0 +
r
v0
y
y0
1
(v )
2
g
0 2
y
θ
ymax
x
Fig. 3.5
x0
0
xmax
R
- Movimento parabólico decorrente
do lançamento oblíquo.
Vamos tomar x0 = y0 = 0 e calcular qual é o alcance do projétil ao
longo do eixo x. Para isto fazemos y = 0 e assim obtemos:
0=
S. C. Zilio e V. S. Bagnato
v 0y
1 gR2
R−
0
vx
2 (v 0 )2
x
Física Básica – Mecânica, calor e ondas
Movimentos bi e tridimensional
41
Descartando a solução R = 0, que corresponde ao início do movimento, temos
R = 2 v 0y v 0x /g , e usando-se v 0y = v 0 sen θ e v 0x = v 0 cos θ obtemos:
R=
v 02 sen (2θ)
g
de onde concluímos que o ângulo que apresenta o maior alcance é θ = 45o
b) Movimento circular
Este deslocamento é caracterizado pelo fato de que o módulo do
deslocamento permanece constante. Assim, imaginamos o raio vetor que
descreve o movimento entre t e t + ∆t. O ângulo ∆θ varrido pelo raio vetor
durante o intervalo de tempo ∆t permite o cálculo da velocidade angular como
ilustrado na Fig. 3.6.
ω=
dθ
∆θ
= lim ∆t →0
dt
∆t
y
∆θ
t+∆t
θ
t
x
Fig. 3.6 – Movimento circular.
Quando ω é constante, temos θ =
∫
t
0
ω dt = ωt e assim podemos
escrever: x = r cosωt e y = r senωt, ou em notação vetorial:
r
r = r cos ωt î + rsenωt ˆj
r
r
v = d r = − rωsenωt î + rω cos ωt ĵ
dt
r dvr
r
a=
= − rω2 cos ωt î − rω2senωt ˆj = −ω2 r
dt
S. C. Zilio e V. S. Bagnato
Mecânica, calor e ondas
Movimentos bi e tridimensional
42
r
que é sempre oposta a direção radial. Portanto, a = a = ω 2 r = v 2 / r visto
r
que v = r ω e esta aceleração é conhecida como “centrípeta” por estar
dirigida ao ponto central do movimento e é uma característica importante do
movimento circular uniforme.
c) Movimento ciclóide
É o movimento de um ponto da borda de um disco rodando, conforme
mostra a Fig. 3.7. Considerando um sistema de eixos no qual x é paralelo ao
chão, temos a combinação de um movimento translacional uniforme com um
movimento circular uniforme. Para o movimento translacional, xt = x0 + vxt e,
para o movimento circular, x0 = r cosωt e y0 = r senωt.
r
x
Fig. 3.7 - Movimento ciclóide.
Desta forma,
x = x 0 + v x t + r cos ωt
y = y 0 + r sen ωt
Ao utilizarmos a notação vetorial e fazendo x0 = y0 = 0,
r
r = (v x t + r cos ωt ) î + r sen ωt ĵ
S. C. Zilio e V. S. Bagnato
Física Básica – Mecânica, calor e ondas
Movimentos bi e tridimensional
43
r
r
v = d r = ( v x − rωsenωt ) î + rω cos ωt ĵ
dt
r dvr
r
a=
= − rω2 cos ωt î − rω2senωt ĵ = −ω2 rc
dt
Exemplo: Considere um disco descendo um plano inclinado,
formando um ângulo θ com a horizontal, como mostrado na Fig. 3.8. Vamos
determinar x(t) e y(t) de um ponto localizado na borda do disco. Escolhendo o
eixo x da maneira indicada na figura, temos ax = g senθ e ay = 0. Então, x = xt
+ xc, y = yt + yc
1
⇒ x = v 0x t + g sen θ t 2 + r cos β e y = v 0y t + r sen β ,
2
onde β ≠ ωt (movimento acelerado) é o ângulo que o disco rodou.
P
r
x
θ
Fig. 3.8 – Disco descendo um plano inclinado
3.4 Movimentos planos descritos por coordenadas
polares
Vamos considerar um movimento circular no qual o corpo percorre
um comprimento de arco s, que está associado a um ângulo θ de acordo com: s
= rθ, sendo r o raio da trajetória. A velocidade tangencial é:
v=
S. C. Zilio e V. S. Bagnato
ds
dθ
=r
= rω
dt
dt
Mecânica, calor e ondas
Movimentos bi e tridimensional
44
r
Para representar v , vamos introduzir os versores r̂ e θ̂ , que são
adequados para se trabalhar com coordenadas polares. O versor r̂ tem a
r
r
mesma direção e sentido do vetor posição r . O versor θ̂ é perpendicular a r
e tangente ao círculo, apontando para a direção em que θ e s crescem como
r
r
indica a Fig. 3.9. Desta forma, podemos escrever r e v em coordenadas
polares da seguinte maneira:
r
r = r r̂
r
dθ
v = v θˆ = r θˆ
dt
y
θ̂
r̂
r
r
θ
ĵ
x
î
Fig. 3.9 – Movimento plano descrito por coordenadas polares.
Devemos notar que r̂ e θ̂ são versores que variam com o tempo. Para
encontrar esta variação em termos dos versores î e ĵ que são fixos vemos
que r̂ = cos θ î + sen θ ĵ e θˆ = − sen θ î + cos θ ĵ . Desta forma,
(
)
dr̂
dθ
dθ
dθ
dθ ˆ
= − sen θ î + cos θ ĵ =
− sen θ î + cos θ ĵ =
θ
dt
dt
dt
dt
dt
(
)
dθˆ
dθ
dθ
=−
cos θ î + sen θ ĵ = −
r̂
dt
dt
dt
Uma vez que conhecemos a maneira pela qual r̂ e θ̂ variam com o
r
r r
tempo, podemos encontrar v e a a partir de r .
S. C. Zilio e V. S. Bagnato
Física Básica – Mecânica, calor e ondas
Movimentos bi e tridimensional
45
r
r = r r̂
r
r dr
dr̂
dθ
= r = r θˆ
v=
dt
dt
dt
r
2
ˆ
r dv
dθ dθ
 dθ 
=r
= − r   r̂
a=
dt
dt dt
 dt 
onde foi suposto que ω = dθ/dt é constante. Como dθ/dt = v/r, temos
r
a = −(v 2 /r ) r̂ = −ω 2 r r̂ , que é a aceleração centrípeta no movimento circular
uniforme.
Se o movimento for uniformemente acelerado, isto é, se dω/dt = α =
constante, a expressão para a aceleração se modifica. Tomando a derivada de
r
v = ωr θˆ temos:
 dω ˆ
r
dθˆ 
a = r 
θ + ω  = r α θˆ −ω 2 r r̂
dt 
 dt
de onde vemos que além da aceleração centrípeta surge uma aceleração
tangencial dada por r α θˆ .
A descrição de um movimento retilíneo através de coordenadas
polares é feita baseando-se na Fig. 3.10. Podemos relacionar vr e vθ da
seguinte forma:
vx = vr cosθ - vθ senθ
vy = vr cosθ + vθ senθ
ou
vr = vx cosθ + vy senθ
vθ = -vx senθ + vy cosθ
r̂
θ̂
y
r
r
θ
vy
r
v
vθ
x
θ
vr
θ
vx
Fig. 3.10 – Descrição de um movimento retilíneo através de coordenadas polares.
S. C. Zilio e V. S. Bagnato
Mecânica, calor e ondas
Movimentos bi e tridimensional
46
Para o caso que estamos tratando, vx = v e vy = 0. Portanto, vr = v
cosθ e vθ = v senθ, ou seja:
r
v = v cos θ r̂ − v sen θ θˆ
Exercícios
1 – Considere um cilindro de raio R rolando sem deslizar num plano
horizontal. O centro de massa do cilindro possui aceleração a. Qual é a
aceleração angular do cilindro? Qual é o ângulo β que o cilindro roda
como função do tempo?
2 – Dois corpos A e B estão em movimentos circular uniformes de trajetórias
concêntricas com raios ra e rb e velocidades angulares ωa e ωb. Determine
a velocidade relativa entre os dois corpos.
3 – Determinar a aceleração de um corpo que desliza pela rosca de um
parafuso com passo h e raio R. Despreze o atrito e considere que o corpo
partiu do repouso.
4 – É necessário lançar da terra uma bola por cima de uma parede de altura H
que se encontra a uma distância S (Fig. 3.11). Qual é a menor velocidade
inicial com que a bola pode ser lançada?
H
r
v0
S
Fig. 3.11 – Lançamento de projétil sobre uma parede de altura H.
S. C. Zilio e V. S. Bagnato
Física Básica – Mecânica, calor e ondas
Movimentos bi e tridimensional
47
5 – Uma bala é disparada de um canhão com velocidade v0. Determine a
região geométrica onde a bala certamente não cairá.
6 – Um plano inclinado forma um ângulo α com o plano xy, conforme mostra
a Fig. 3.12. Um corpo é lançado com velocidade v0, formando um ângulo
θ com o eixo y. Desprezando o atrito calcule: xmax, zmax e o tempo que o
projétil demora para retornar ao eixo y.
7 – Uma pedra é lançada com velocidade inicial de 20 m/s. Sabendo-se que ela
ficou 2 s no ar, calcule:
a) o ângulo de lançamento (com a horizontal)
b) a altura máxima atingida
c) o alcance
d) outro ângulo de lançamento para o qual a pedra terá o mesmo alcance.
(Neste caso o tempo será diferente de 2 s).
z
r
v0
θ
α
y
x
Fig. 3.12 – Lançamento oblíquo num plano inclinado.
8 – Um corpo translada com velocidade v = 5 m/s sobre um plano horizontal
sem atrito. Subitamente ele encontra pela frente um plano inclinado
(também sem atrito) de ângulo θ = 300 e altura H = 0,8 m, conforme
mostra a Fig. 3.13. Tomando-se g = 10 m/s, pergunta-se:
a) a que distância d do final do plano inclinado o corpo cairá?
b) qual é a altura máxima que o corpo atingirá?
S. C. Zilio e V. S. Bagnato
Mecânica, calor e ondas
Movimentos bi e tridimensional
48
ymax
H
r
v
x
θ
d
Fig. 3.13 - Lançamento oblíquo de um corpo por meio de uma rampa.
9 – Um pequeno corpo é lançado da origem com velocidade v0 = 100/ 3 m/s
formando um ângulo θ = 600 com a horizontal. Outro corpo é lançado 1
segundo depois, com a mesma velocidade v0, porém na horizontal e de
uma altura H, como mostra a Fig. 3.14. Suponha que haja uma colisão
entre os dois corpos e que g = 10 m/s2.
a) Em que instante de tempo ocorre a colisão?
b) Qual deve ser o valor de H para que a colisão ocorra?
c) Quais as coordenadas x e y da colisão?
3.10 – Um pequeno corpo é lançado da origem com velocidade v0 segundo um
ângulo θ com a horizontal. Outro corpo é lançado com a mesma
velocidade v0, porém na horizontal e de uma altura H, como mostra a
Fig. 3.14. Qual deve ser o valor de H tal que eles atinjam o mesmo
ponto no eixo Ox?
v0
H
v0
θ
O
x
Fig. 3.14 - Lançamento de dois corpos.
S. C. Zilio e V. S. Bagnato
Física Básica – Mecânica, calor e ondas
Movimentos bi e tridimensional
49
3.11 - Mostre que o movimento de um projétil lançado com v0 e θ é descrito
2
v 0y 
g x
 , com v0x = v0 cosθ e v0y = v0
pela parábola: y ( x ) =
− 
−
2 g 2  v 0x
g 
v 0y 2
senθ. b) Encontre o ângulo α que a trajetória faz com a horizontal para
qualquer x (tgα = dy/dx), c) Encontre xmax correspondente ao topo da trajetória
(tg α = 0). d) Encontre o alcance R, fazendo α = π−θ
S. C. Zilio e V. S. Bagnato
Mecânica, calor e ondas
50
S. C. Zilio e V. S. Bagnato
Movimentos bi e tridimensional
Física Básica – Mecânica, calor e ondas