Aula 4 - Regra de três simples

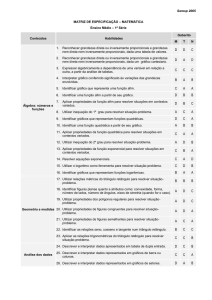
Matemática Básica
Regra de Três Simples
Prof.: Joni Fusinato
[email protected]
[email protected]
1
Grandezas Diretamente Proporcionais
 Duas grandezas são ditas diretamente proporcionais quando o
aumento de uma acarreta no aumento da outra, ou ainda, quando
uma diminuição em uma gera uma diminuição na outra grandeza.
Grandezas Inversamente Proporcionais
 Duas grandezas são chamadas de inversamente proporcionais
quando a diminuição de uma acarreta no aumento da outra, e
vice-versa.
Regra de Três Simples
 Processo prático para resolver problemas que envolvam quatro
grandezas (valores) dos quais conhecemos três delas.
 Como montar uma regra de três simples:
 Construir uma tabela, agrupando as grandezas em colunas relacionando
cada valor a sua grandeza;
 Identificar se as grandezas são diretamente ou inversamente
proporcionais;
 Montar a equação da seguinte maneira: se as grandezas forem
diretamente proporcionais, multiplica-se os valores em forma de X; se
as grandezas forem inversamente proporcionais, multiplica-se os
valores em linha. Também pode se inverter uma das colunas.
 Resolver a equação.
Exemplo 1
Uma mãe recorreu à bula para verificar a dosagem de um remédio que
precisava dar a seu filho. Na bula, recomendava-se a seguinte dosagem:
5 gotas para cada 2 kg de massa corporal a cada 8 horas.
Se a mãe ministrou corretamente 30 gotas do remédio a seu filho a cada
8 horas, então a massa corporal dele é de:
a) 12 kg.
b) 16 kg.
c) 24 kg.
d) 36 kg.
e) 75 kg.
Se aumenta as gotas o peso
também deve aumentar.
Grandezas diretamente
proporcionais.
5·x = 2·30
5·x = 60
x = 60/5
x = 12 kg
5
Exemplo 2:
Qual a dosagem de Decadron que deve ser ministrado para um paciente que
apresenta uma prescrição médica solicitando administrar 0,8 mg desse
medicamento?
Apresentação do medicamento: frasco de 2,5 ml com 10 mg.
ml
mg
2,5
10
x
0,8
10.x = 0,8.2,5
x = 2/10
x = 0,2 ml.
Se diminui as mg também diminui os ml.
Grandezas diretamente proporcionais.
Agora é a sua vez!
1) Uma usina produz 500 litros de álcool com 6.000 kg de cana de
açúcar. Quantos litros de álcool serão produzidos com 15.000 kg
de cana?
2) Na conta de água de uma residência consta o consumo mensal de
25,6 m3. Quantos litros de água foram usados nessa residência?
(1 m3 = 1.000 l)
7
Exemplo 3
Se 5 operários levantam um muro em 10 dias, quantos operários
serão necessários para levantar o mesmo muro em 2 dias?
Como as grandezas são inversamente
proporcionais, multiplica-se os valores em
linha ou inverte-se uma das colunas e
depois multiplica-se em cruz.
2.x = 5.10
x = 50/2
x = 25 operários
8
Exemplo 4
Uma equipe de operários, trabalhando 8 horas por dia, realizou uma obra
em 20 dias. Se o número de horas de serviço for reduzido para 5 horas,
em que prazo essa equipe fará o mesmo trabalho?
Horas
Prazo (dias)
8
5
20
x
Como as grandezas são inversamente
proporcionais, multiplica-se os valores em
linha ou inverte-se uma das colunas e
depois multiplica-se em cruz.
Macete: quando as palavras são contrárias (diminuindo - aumenta), as grandezas
são inversamente proporcionais.
Agora é a sua vez!
1) Em uma panificadora são produzidos 90 pães de 50 gramas cada
um. Caso queira produzir pães com 45 gramas, quantos pães serão
produzidos?
2) Uma equipe de 5 professores gastaram 12 dias para corrigir as
provas de um vestibular. Considerando a mesma proporção, quantos
dias levarão 30 professores para corrigir as provas?
10