Programação Paralela e Distribuída Métricas de Desempenho

Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Programação
Paralela e Distribuída
Métricas de Desempenho
1
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Desempenho
Dois dos principais objectivos do desenho de aplicações paralelas são:
Desempenho: a capacidade de reduzir o tempo de resolução do problema à medida que
os recursos computacionais aumentam.
Escalabilidade: a capacidade de aumentar o desempenho à medida que a complexidade
do problema aumenta.
Os factores que condicionam o desempenho e a escalabilidade de uma aplicação são:
Limites Arquitecturais
Limites Algorítmicos
Ricardo Rocha DCC-FCUP
2
1
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Limites ao Desempenho
Limites Arquitecturais
Latência e Largura de Banda
Coerência dos Dados
Capacidade de Memória
Limites Algorítmicos
Falta de Paralelismo (código sequencial/concorrência)
Frequência de Comunicação
Frequência de Sincronização
Escalonamento Deficiente (granularidade das tarefas/balanceamento de carga)
3
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métricas de Desempenho
Existem 2 classes distintas de métricas de desempenho:
Métricas de Desempenho para Processadores: métricas que permitem avaliar a
performance de um processador tendo por base a velocidade/número de operações que
este consegue realizar num determinado espaço temporal.
Métricas de Desempenho para Aplicações Paralelas: métricas que permitem avaliar a
performance de uma aplicação paralela tendo por base a comparação entre a execução
com múltiplos processadores e a execução com um só processador.
No nosso caso, estamos obviamente mais interessados nas métricas que permitem
avaliar o desempenho das aplicações paralelas.
Ricardo Rocha DCC-FCUP
4
2
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métricas de Desempenho para Processadores
Algumas das métricas mais conhecidas para medir o desempenho da arquitectura de
um processador/computador são:
MIPS: acrónimo para Millions of Instructions Per Second.
FLOPS: acrónimo para FLoating point Operations Per Second.
SPECint: conjunto de programas de teste (benchmarks) da SPEC (Standard Performance
Evaluation Corporation) que avaliam o desempenho do processador em aritmética de
inteiros (1992).
SPECfp: conjunto de programas de teste da SPEC que avaliam o desempenho do
processador em operações de vírgula flutuante (2000).
Whetstone: programa de teste sintético que avalia o desempenho do processador em
operações de vírgula flutuante (1972).
Dhrystone: programa de teste sintético que avalia o desempenho do processador em
aritmética de inteiros (1984).
5
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métricas de Desempenho para Aplicações Paralelas
Existem várias medidas que permitem medir/avaliar o desempenho duma aplicação
paralela. As mais conhecidas são:
Speedup
Eficiência
Redundância
Utilização
Qualidade
Existem igualmente várias leis/métricas que permitem balizar o comportamento duma
aplicação paralela face ao seu potencial desempenho. As mais conhecidas são:
Lei de Amdahl
Lei de Gustafson-Barsis
Métrica de Karp-Flatt
Métrica de Isoeficiência
Ricardo Rocha DCC-FCUP
6
3
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Speedup
O speedup é uma medida do grau de desempenho. O speedup mede o rácio entre o
tempo de execução sequencial e o tempo de execução em paralelo.
S ( p) =
T (1)
T ( p)
T(1) é o tempo de execução com um processador
T(p) é o tempo de execução com p processadores
1 CPU
2 CPUs
4 CPUs
8 CPUs
16 CPUs
T(p)
1000
520
280
160
100
S(p)
1
1,92
3,57
6,25
10,00
7
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Eficiência
A eficiência é uma medida do grau de aproveitamento dos recursos computacionais.
A eficiência mede o rácio entre o grau de desempenho e os recursos computacionais
disponíveis.
E ( p) =
S ( p)
T (1)
=
p
p × T ( p)
S(p) é o speedup para p processadores
1 CPU
2 CPUs
4 CPUs
8 CPUs
16 CPUs
S(p)
1
1,92
3,57
6,25
10,00
E(p)
1
0,96
0,89
0,78
0,63
Ricardo Rocha DCC-FCUP
8
4
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Redundância
A redundância é uma medida do grau de aumento da computação. A redundância
mede o rácio entre o número de operações realizadas pela execução paralela e pela
execução sequencial.
R( p) =
O( p)
O (1)
O(1) é o número total de operações realizadas com 1 processador
O(p) é o número total de operações realizadas com p processadores
1 CPU
2 CPUs
4 CPUs
8 CPUs
16 CPUs
O(p)
10000
10250
11000
12250
15000
R(p)
1
1,03
1,10
1,23
1,50
9
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Utilização
A utilização é uma medida do grau de aproveitamento da capacidade computacional.
A utilização mede o rácio entre a capacidade computacional utilizada durante a
computação e a capacidade disponível.
U ( p) = R( p) × E ( p)
1 CPU
2 CPUs
4 CPUs
8 CPUs
16 CPUs
R(p)
1
1,03
1,10
1,23
1,50
E(p)
1
0,96
0,89
0,78
0,63
U(p)
1
0,99
0,98
0,96
0,95
Ricardo Rocha DCC-FCUP
10
5
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Qualidade
A qualidade é uma medida do grau de importância de utilizar programação paralela.
Q( p) =
S ( p) × E ( p)
R( p)
1 CPU
2 CPUs
4 CPUs
8 CPUs
16 CPUs
S(p)
1
1,92
3,57
6,25
10,00
E(p)
1
0,96
0,89
0,78
0,63
R(p)
1
1,03
1,10
1,23
1,50
Q(p)
1
1,79
2,89
3,96
4,20
11
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Lei de Amdahl
A computação realizada por uma aplicação paralela pode ser divididas em 3 classes:
C(seq): computações que só podem ser realizadas sequencialmente.
C(par): computações que podem ser realizadas em paralelo.
C(com): computações de comunicação/sincronização/iniciação.
Usando estas 3 classes, o speedup de uma aplicação pode definido do seguinte
modo:
S ( p) =
Ricardo Rocha DCC-FCUP
T (1)
C ( seq) + C ( par )
=
T ( p ) C ( seq) + C ( par ) + C (com)
p
12
6
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Lei de Amdahl
Como C(com) ≥ 0 então:
S ( p) ≤
C ( seq) + C ( par )
C ( par )
C ( seq) +
p
Se f for a fracção da computação que só pode ser realizada sequencialmente então:
f =
C ( seq)
C ( seq) + C ( par )
S ( p) ≤
e
C ( seq)
f
⎛1 ⎞
C ( seq) × ⎜⎜ − 1⎟⎟
⎝f
⎠
C ( seq) +
p
13
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Lei de Amdahl
Simplificando:
S ( p) ≤
⇒
C ( seq)
f
⎛1 ⎞
C ( seq ) × ⎜⎜ − 1⎟⎟
⎝f
⎠
C ( seq) +
p
1
1
f
S ( p) ≤
⇒
S ( p) ≤
1
1− f
−1
f+
f
p
1+
p
Ricardo Rocha DCC-FCUP
14
7
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Lei de Amdahl
Seja 0 ≤ f ≤ 1 a fracção da computação que só pode ser realizada sequencialmente. A
lei de Amdahl diz-nos que o speedup máximo que uma aplicação paralela com p
processadores pode obter é:
S ( p) ≤
1
1− f
f+
p
A lei de Amdahl dá-nos uma medida do speedup máximo que podemos obter ao
resolver um determinado problema com p processadores.
A lei de Amdahl também pode ser utilizada para determinar o limite máximo de
speedup que uma determinada aplicação poderá alcançar independentemente do
número de processadores a utilizar.
15
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Lei de Amdahl
Suponha que pretende determinar se é vantajoso desenvolver uma versão paralela de
uma determinada aplicação sequencial. Por experimentação, verificou-se que 90%
do tempo de execução é passado em procedimentos que se julga ser possível
paralelizar. Qual é o speedup máximo que se pode alcançar com uma versão paralela
do problema executando em 8 processadores?
S ( p) ≤
1
≈ 4,71
1 − 0,1
0,1 +
8
E o limite máximo de speedup que se pode alcançar?
1
= 10
p →∞
1 − 0,1
0,1 +
p
lim
Ricardo Rocha DCC-FCUP
16
8
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Limitações da Lei de Amdahl
A lei de Amdahl ignora o custo das operações de comunicação/sincronização
associadas à introdução de paralelismo numa aplicação. Por esse motivo, a lei de
Amdahl pode resultar em predições pouco realísticas para determinados problemas.
Suponha que desenvolveu uma aplicação paralela cujo padrão de execução é o
seguinte, em que n é o tamanho do problema:
Tempo de execução da parte sequencial (input e output de dados):
Tempo de execução da parte paralelizável:
18.000 + n
n2
100
Total de pontos de comunicação/sincronização por processador:
Tempo de execução por comunicação/sincronização:
⎡log n⎤
10.000 × ⎡log p ⎤ +
n
10
17
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Limitações da Lei de Amdahl
Qual é o speedup máximo que se pode obter?
Utilizando a lei de Amdahl:
f =
18.000 + n
n2
18.000 + n +
100
n2
100
S ( p) ≤
n2
18.000 + n +
p × 100
18.000 + n +
e
Utilizando a medida de speedup:
n2
100
S ( p) =
2
n
n⎞
⎛
18.000 + n +
+ ⎡log n ⎤ × ⎜10.000 × ⎡log p ⎤ + ⎟
p × 100
10 ⎠
⎝
18.000 + n +
Ricardo Rocha DCC-FCUP
18
9
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Limitações da Lei de Amdahl
Lei de
Amdahl
Speedup
1 CPU
2 CPUs
4 CPUs
8 CPUs
16 CPUs
n = 10.000
1
1,95
3,70
6,72
11,36
n = 20.000
1
1,98
3,89
7,51
14,02
n = 30.000
1
1,99
3,94
7,71
14,82
n = 10.000
1
1,61
2,11
2,22
2,57
n = 20.000
1
1,87
3,21
4,71
6,64
n = 30.000
1
1,93
3,55
5,89
9,29
19
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Lei de Gustafson-Barsis
Consideremos novamente a medida de speedup definida anteriormente:
S ( p) ≤
C ( seq) + C ( par )
C ( par )
C ( seq) +
p
Se f for a fracção da computação paralela realizada a executar computações
sequenciais então:
f =
C ( seq)
C ( par )
C ( seq) +
p
Ricardo Rocha DCC-FCUP
e
C(par)
p
(1 − f ) =
C(par)
C(seq) +
p
20
10
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Lei de Gustafson-Barsis
Logo:
⎛
C ( par ) ⎞
⎟
C ( seq) = f × ⎜⎜ C ( seq) +
p ⎟⎠
⎝
⎛
C ( par ) ⎞
⎟
C ( par ) = p × (1 − f ) × ⎜⎜ C ( seq) +
p ⎟⎠
⎝
Simplificando:
⎛
C ( par ) ⎞
⎟
+ p × (1 − f ))× ⎜⎜ C ( seq) +
p ⎟⎠
⎝
S ( p) ≤
C ( par )
C ( seq) +
p
S ( p ) ≤ f + p × (1 − f )
S ( p ) ≤ p + f × (1 − p )
⇒
(f
⇒
21
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Lei de Gustafson-Barsis
Seja 0 ≤ f ≤ 1 a fracção da computação paralela realizada a executar computações
sequenciais. A lei de Gustafson-Barsis diz-nos que o speedup máximo que uma
aplicação paralela com p processadores pode obter é:
S ( p ) ≤ p + f × (1 − p )
Enquanto a lei de Amdahl parte do tempo de execução sequencial para estimar o
speedup máximo passível de ser conseguido em múltiplos processadores, a lei de
Gustafson-Barsis faz precisamente o contrário, ou seja, parte do tempo de execução
em paralelo para estimar o speedup máximo comparado com a execução sequencial.
Ricardo Rocha DCC-FCUP
22
11
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Lei de Gustafson-Barsis
Considere que uma determinada aplicação executa em 220 segundos em 64
processadores. Qual é o speedup máximo da aplicação sabendo que por
experimentação verificou-se que 5% do tempo de execução é passado em
computações sequenciais.
S ( p) ≤ 64 + (0,05) × (1 − 64) = 64 − 3,15 = 60,85
Suponha que uma determinada companhia pretende comprar um supercomputador
com 16.384 processadores de modo a obter um speedup de 15.000 num problema de
fundamental importância. Qual é a fracção máxima da execução paralela que pode
ser passada em computações sequenciais de modo a se atingir o speedup pretendido?
15.000 ≤ 16.384 + f × (1 − 16.384)
f × 16.383 ≤ 1.384
f ≤ 0,084
23
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Limitações da Lei de Gustafson-Barsis
Ao usar o tempo de execução em paralelo como o ponto de partida, em lugar do
tempo de execução sequencial, a lei de Gustafson-Barsis assume que a execução
com um só processador é no pior dos casos p vezes mais lenta que a execução com p
processadores.
Isso pode não ser verdade se a memória disponível para a execução com um só
processador for insuficiente face à computação realizada pelos p processadores. Por
este motivo, o speedup estimado pela lei de Gustafson-Barsis é habitualmente
designado por scaled speedup.
Ricardo Rocha DCC-FCUP
24
12
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Karp-Flatt
Consideremos novamente a definição do tempo de execução sequencial e do tempo
de execução em paralelo:
T (1) = C ( seq) + C ( par )
C ( par )
T ( p ) = C ( seq) +
+ C (com)
p
Seja e a fracção sequencial determinada experimentalmente duma computação
paralela:
e=
C ( seq)
T (1)
25
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Karp-Flatt
Logo:
C ( seq) = e × T (1)
C ( par ) = (1 − e) × T (1)
Se considerarmos que C(com) é desprezável então:
T ( p) = e × T (1) +
(1 − e) × T (1)
p
Por outro lado:
T (1)
T ( p)
T (1) = S ( p) × T ( p)
S ( p) =
⇒
Ricardo Rocha DCC-FCUP
26
13
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Karp-Flatt
Simplificando:
(1 − e) × S ( p ) × T ( p )
p
(1 − e) × S ( p )
1 = e × S ( p) +
p
1
(1 − e)
1
1 e
= e+
⇒
= e+ −
S ( p)
p
S ( p)
p p
1
1
−
⎛ 1⎞ 1
1
S ( p) p
⇒
e=
= e × ⎜⎜1 − ⎟⎟ +
1
S ( p)
p⎠ p
⎝
1−
p
T ( p) = e × S ( p) × T ( p) +
⇒
⇒
⇒
27
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Karp-Flatt
Seja S(p) o speedup duma aplicação paralela com p > 1 processadores. A métrica de
Karp-Flatt diz-nos que a fracção sequencial determinada experimentalmente é:
1
1
−
S ( p) p
e=
1
1−
p
A métrica de Karp-Flatt é interessante porque ao desprezar o custo das operações de
comunicação/sincronização/iniciação associadas à introdução de paralelismo numa
aplicação, permite-nos determinar à posteriori qual a importância da componente
C(com) no eventual decréscimo de eficiência da aplicação.
Ricardo Rocha DCC-FCUP
28
14
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Karp-Flatt
Por definição, a fracção sequencial determinada experimentalmente é um valor
constante que não depende do número de processadores.
e=
C ( seq)
T (1)
Por outro lado, a métrica de Karp-Flatt é uma função do número de processadores.
1
1
−
S ( p) p
e=
1
1−
p
29
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Karp-Flatt
Como a eficiência duma aplicação é uma função decrescente do número de
processadores, a métrica de Karp-Flatt permite-nos determinar qual a importância da
componente C(com) nesse decréscimo.
Se os valores de e forem constantes à medida que o número de processadores aumenta
isso significa que a componente C(com) é também constante. Logo, o decréscimo da
eficiência é devido à existência de pouco paralelismo no problema.
Se os valores de e aumentarem à medida que o número de processadores aumenta isso
significa que o decréscimo é devido à componente C(com), ou seja, à existência de custos
excessivos associados à computação em paralelo (custos de comunicação, sincronização
e/ou iniciação da computação).
Ricardo Rocha DCC-FCUP
30
15
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Karp-Flatt
Por exemplo, a métrica de Karp-Flatt permite-nos detectar fontes de ineficiência não
consideradas pelo modelo que assume que p processadores executam a parte que
pode ser paralelizável p vezes mais rápido do que a execução com um só
processador.
Se tivermos 5 processadores para resolver um problema decomposto em 20 tarefas
indivisíveis, todos os processadores podem executar 4 tarefas. Se todas as tarefas
demorarem o mesmo tempo a executar então o tempo de execução em paralelo será uma
razão de 4.
Por outro lado, se tivermos 6 processadores para resolver o mesmo problema, 4
processadores podem executar 3 tarefas mas dois deles terão necessariamente de executar
4. Isto faz com que o tempo de execução em paralelo seja igualmente uma razão de 4 e
não uma razão de 20/6.
31
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Karp-Flatt
Considere os seguintes speedups obtidos por uma determinada aplicação paralela:
2 CPUs
3 CPUs
4 CPUs
5 CPUs
6 CPUs
7 CPUs
8 CPUs
S(p)
1,82
2,50
3,08
3,57
4,00
4,38
4,71
e
0,099
0,100
0,100
0,100
0,100
0,100
0,100
Qual é a principal razão para a aplicação obter apenas um speedup de 4,71 com 8
processadores?
Como e não aumenta com o número de processadores, isso significa que a principal razão
para o baixo speedup é a falta de paralelismo existente no problema.
Ricardo Rocha DCC-FCUP
32
16
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Karp-Flatt
Considere os seguintes speedups obtidos por uma determinada aplicação paralela:
2 CPUs
3 CPUs
4 CPUs
5 CPUs
6 CPUs
7 CPUs
8 CPUs
S(p)
1,87
2,61
3,23
3,73
4,14
4,46
4,71
e
0,070
0,075
0,079
0,085
0,090
0,095
0,100
Qual é a principal razão para a aplicação obter apenas um speedup de 4,71 com 8
processadores?
Como e aumenta ligeiramente com o número de processadores, isso significa que a
principal razão para o baixo speedup são os custos associados à computação em paralelo.
33
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Eficiência e Escalabilidade
Dos resultados anteriores podemos concluir que a eficiência duma aplicação é:
Uma função decrescente do número de processadores.
Tipicamente uma função crescente do tamanho do problema.
Ricardo Rocha DCC-FCUP
34
17
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Eficiência e Escalabilidade
Uma aplicação é dita de escalável quando demonstra a capacidade de manter a
mesma eficiência à medida que o número de processadores e a complexidade do
problema aumentam proporcionalmente.
A escalabilidade duma aplicação reflecte a sua capacidade de utilizar mais recursos
computacionais de forma efectiva.
1 CPU
2 CPUs
4 CPUs
8 CPUs
16 CPUs
n = 10.000
1
0,81
0,53
0,28
0,16
Eficiência n = 20.000
1
0,94
0,80
0,59
0,42
n = 30.000
1
0,96
0,89
0,74
0,58
35
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Isoeficiência
A eficiência duma aplicação é tipicamente uma função crescente do tamanho do
problema porque a complexidade de comunicação é habitualmente inferior à
complexidade da computação, ou seja, a forma de manter o mesmo nível de
eficiência quando aumentamos o número de processadores é aumentar o
tamanho do problema. A métrica de isoeficiência formaliza esta ideia.
Consideremos novamente a medida de speedup definida anteriormente:
S ( p) =
C ( seq) + C ( par )
p × (C ( seq) + C ( par ) )
=
C ( par )
C ( seq) +
+ C (com) p × C ( seq) + C ( par ) + p × C (com)
p
p × (C ( seq) + C ( par ) )
=
C ( seq) + C ( par ) + ( p − 1) × C ( seq) + p × C (com)
Ricardo Rocha DCC-FCUP
36
18
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Isoeficiência
Seja T0(p) o tempo de execução dispendido pelos p processadores do algoritmo
paralelo a realizar computações não realizadas pelo algoritmo sequencial:
T0 ( p ) = ( p − 1) × C ( seq) + p × C (com)
Simplificando:
S ( p) =
E ( p) =
p × (C ( seq) + C ( par ) )
C ( seq) + C ( par ) + T0 ( p )
C ( seq) + C ( par )
=
C ( seq) + C ( par ) + T0 ( p ) 1 +
1
1
=
T0 ( p )
T ( p)
1+ 0
C ( seq) + C ( par )
T (1)
37
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Isoeficiência
Então:
1
T ( p)
1+ 0
T (1)
T0 ( p) 1 − E ( p)
=
T (1)
E ( p)
E ( p) =
⇒
⇒
T (1) =
E ( p)
× T0 ( p )
1 − E ( p)
Se pretendermos manter o mesmo nível de eficiência quando aumentamos o número
de processadores então:
E ( p)
=c
1 − E ( p)
Ricardo Rocha DCC-FCUP
e
T (1) ≥ c × T0 ( p)
38
19
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Isoeficiência
Seja E(p) a eficiência duma aplicação paralela com p processadores. A métrica de
isoeficiência diz-nos que para se manter o mesmo nível de eficiência quando
aumentamos o número de processadores então o tamanho do problema deve ser
aumentado de forma a que a seguinte desigualdade seja satisfeita:
T (1) ≥ c × T0 ( p )
em que c =
E ( p)
e T0 ( p ) = ( p − 1) × C ( seq) + p × C (com)
1 − E ( p)
A aplicação da métrica de isoeficiência pode depender da quantidade de memória
disponível, pois o tamanho máximo do problema que pode ser resolvido é limitado
por essa quantidade.
39
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Isoeficiência
Suponha que a métrica de isoeficiência para um problema de tamanho n nos é dada
por uma função do número de processadores p:
n ≥ f ( p)
Se M(n) designar a quantidade de memória necessária para resolver o problema de
tamanho n então:
n ≥ M ( f ( p) )
Ou seja, para se manter o mesmo nível de eficiência, a quantidade de memória
necessária por processador é:
M ( f ( p) )
p
Ricardo Rocha DCC-FCUP
40
20
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
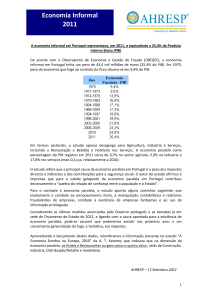
Métrica de Isoeficiência
c × p × log p
Memória por processador
Eficiência não pode ser
c× p
mantida e deve decrescer
limite de memória
c × log p
Eficiência pode
ser mantida
c
Número de processadores
41
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Métrica de Isoeficiência
Considere que a versão sequencial de uma determinada aplicação tem complexidade
O(n3) e que o tempo de execução dispendido por cada um dos p processadores da
versão paralela em operações de comunicação/sincronização é O(n2 log p). Se a
quantidade de memória necessária para representar um problema de tamanho n for
n2, qual é a escalabilidade da aplicação em termos de memória?
n 3 ≥ c × p × n 2 × log p
n ≥ c × p × log p
M ( n) = n
2
⇒
M (c × p × log p) c 2 × p 2 × log 2 p
=
= c 2 × p × log 2 p
p
p
Logo, a escalabilidade da aplicação é baixa.
Ricardo Rocha DCC-FCUP
42
21
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Speedup Superlinear
O speedup diz-se superlinear quando o rácio entre o tempo de execução sequencial e
o tempo de execução em paralelo com p processadores é maior do que p.
T (1)
≥p
T ( p)
Alguns dos factores que podem fazer com que o speedup seja superlinear são:
Custos de comunicação/sincronização/iniciação praticamente inexistentes.
Tolerância à latência da comunicação.
Aumento da capacidade de memória (o problema passa a caber todo em memória).
Subdivisão do problema (tarefas menores geram menos cache misses).
Aleatoriedade da computação em problemas de optimização ou com múltiplas soluções.
43
Ricardo Rocha DCC-FCUP
Programação Paralela e Distribuída 2007/08
Métricas de Desempenho
Speedup Superlinear
“Se um único computador (processador) consegue resolver um problema
em N segundos, podem N computadores (processadores)
resolver o mesmo problema em 1 segundo?”
Ricardo Rocha DCC-FCUP
44
22