LISTA DE EXERCÍCIOS #6

LISTA DE EXERCÍCIOS #6 - ELETROMAGNETISMO I
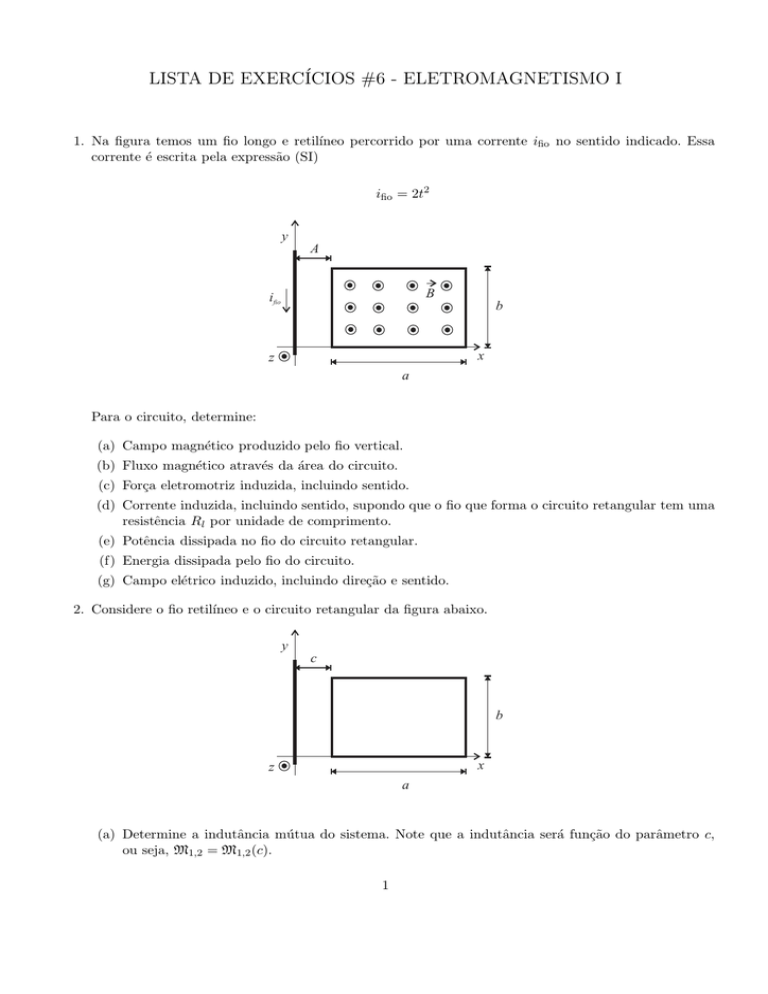
1. Na figura temos um fio longo e retilı́neo percorrido por uma corrente ifio no sentido indicado. Essa
corrente é escrita pela expressão (SI)
ifio = 2t2
y
A
B
ifio
b
x
z
a
Para o circuito, determine:
(a) Campo magnético produzido pelo fio vertical.
(b) Fluxo magnético através da área do circuito.
(c) Força eletromotriz induzida, incluindo sentido.
(d) Corrente induzida, incluindo sentido, supondo que o fio que forma o circuito retangular tem uma
resistência Rl por unidade de comprimento.
(e) Potência dissipada no fio do circuito retangular.
(f) Energia dissipada pelo fio do circuito.
(g) Campo elétrico induzido, incluindo direção e sentido.
2. Considere o fio retilı́neo e o circuito retangular da figura abaixo.
y
c
b
x
z
a
(a) Determine a indutância mútua do sistema. Note que a indutância será função do parâmetro c,
ou seja, M1,2 = M1,2 (c).
1
(b) Sabendo que a força produzida sobre o circuito 1 pelo 2 pode ser dada por
F~1 = −i1 i2 ∇d M2,1 (d)
onde d é um parâmetro que mede distância e que, no problema considerado, corresponde a
distância representada por c, ache a força produzida pelo circuito retangular sobre o fio.
~ = B0 yı̂, conforme mostra a figura abaixo. Uma barra
3. Numa dada região há um campo magnético B
condutora é puxada para a direita e move-se com velocidade constante ~v . A resistência elétrica do
circuito é representada por um resistor de resistência R. O comprimento da barra vale l. Há um
gerador comum (uma bateria ideal) de fem E no circuito. Determine:
A
B
z
B
l
R
Fext
v
y
C
E
x
D
y
(a) Fluxo magnético através do circuito, como função de B0 , l e y.
(b) Força eletromotriz induzida no circuito (incluindo sentido).
(c) Corrente induzida no circuito (incluindo sentido) e corrente total no circuito. Prestar atenção ao
sentido da força externa.
(d) Força magnética agindo na barra.
(e) Força externa que puxa a barra.
4. Determine a energia magnética armazenada dentro de um toróide de seção retangular de lados a e b,
e raios interno e externo Ri e Re , respectivamente, como mostra a figura abaixo, que apresenta um
corte do toróide e algumas espiras. O toróide é formado por N espiras e é percorrido por uma corrente
~
I. Ache U a partir de B.
espiras
Re
Ri
b
a
5. Determine a auto-indutância L de um toróide de seção retangular, como o mostrado no problema 4.
Obs.: Lembrar que há N espiras no toróide.
2
6. Usando os dados do problema anterior, calcule a energia magnética U armazenada no toróide através
de
U=
L i2
2
7. Considere uma região cúbica de 10 cm de lado. Nessa região, estabelece-se inicialmente um campo
elétrico homogêneo de intensidade E = 105 N/C (um campo usual em laboratório). Depois, desliga-se
o campo elétrico e produz-se um campo magnético homogêneo de módulo B = 1,0 T (também usual
em laboratório de pesquisa). Compare as energias armazenadas nos campos produzidos na região. É
mais simples, em termos energéticos, estabelecer um campo elétrico ou magnético?
8. Uma peça metálica maciça é usinada na forma de um toróide de seção reta triangular, conforme mostra
a figura abaixo, que apresenta um corte da peça, para visualização. Ela está disposta paralelamente
ao plano xy, e a origem dos eixos situa-se no centro geométrico da peça. O raio interno do toróide vale
c, e a seção triangular tem lados a e b. Na região central existe um solenóide (não mostrado na figura)
cilı́ndrico, muito longo e de raio R (R < c), cujo eixo coincide com o eixo z, que produz um campo
~ homogêneo (mas não necessariamente constante) apenas na região de raio R, de modo
magnético B
~
que B = B(t) k̂ para ρ ≤ R, onde ρ é a distância de um ponto qualquer do espaço ao eixo z.
z
c
B
R
b
x
y
a
(a) Quando a corrente que circula pelo solenóide varia com o tempo, a peça metálica esquenta.
Explique detalhadamente o motivo.
(b) Considere que a densidade volumétrica mássica da peça seja D, e seja constante. Ache a massa
M da peça.
~
(c) Ache o campo elétrico E~ a uma distância ρ do eixo z mediante a lei de Faraday. Suponha que B
~
~
varie no tempo, de modo que B = B(t). Ache também a fem E induzida na peça.
(d) Considerando que a peça tem uma condutividade σ, determine a densidade de corrente J~ e a
corrente i circulando por ela.
(e) Ache a resistência elétrica R da peça. Pode ser necessário fazer alguma hipótese para esse cálculo.
Se fizer, justifique a hipótese.
(f) Determine a potência elétrica P dissipada na peça.
(g) A peça tem um calor especı́fico C constante. Supondo que toda a potência dissipada na peça seja
convertida em calor, ache a taxa de variação temporal dT
dt da temperatura da peça.
~ = B0 cos(ωt) k̂. Obtenha a forma explı́cita de
(h) Suponha que B
dT
dt
.
(i) Obtenha uma expressão para a temperatura T em função do tempo t, considerando que em t = 0
a peça está a uma temperatura T0 .
3
(j) Faça um gráfico do comportamento de T (t), supondo que a peça é de ferro, onde k = 8,6 g/cm3 ,
R = 1 cm, c = 4 cm, a = 2 cm, b = 1 cm, C = 0,092 kcal/kg.◦ C, σ = 1,4 × 107 S/m, ω = 2πf ,
f = 60 Hz, B0 = 1,0 × 10−2 T e T0 = 25◦ C.
9. A figura mostra um trilho horizontal altamente condutor em forma de U. Uma barra também condutora, de massa M e resistência elétrica R, está apoiada sobre o trilho. Na região há um campo
~ = B0 k̂, que age em toda a região do trilho em U.
magnético uniforme e constante B
z
y
x
v(t)
l
y(t)
(a) Suponha inicialmente que não haja atrito entre a barra e o trilho. Considere que a barra, em t = 0,
esteja localizada na posição y0 , e tenha uma velocidade inicial v0 . Surge corrente no circuito? Qual
é a origem (magnética ou elétrica)? Se houver corrente, determine o seu valor em termos de B0 ,
R, l e v, a velocidade da barra no instante t.
(b) Descreva qualitativamente o movimento da barra, considerando eventuais forças que atuem sobre
a barra. Em seguida, determine v(t) e y(t).
(c) Considerando que v0 = 15 m/s, y0 = 2 m, B0 = 0,4 T, R = 1 Ω, M = 0,2 kg e l = 1,5 m, onde a
barra pára?
(d) Considere agora que haja atrito entre a barra e o trilho, de modo que a força de atrito vale uma
fração α da força magnética inicial agindo na barra. Quanto vale (algebricamente) o coeficiente
de atrito µ? Como ficam as expressões (algébricas) para v(t) e y(t)? Se α = 0,2, quanto vale µ?
10. Manchas solares são regiões na baixa atmosfera solar onde a temperatura é menor do que nas outras
regiões, por isso elas são menos brilhantes em comparação com as regiões mais quentes. Dentro das
manchas há campos magnéticos bastante intensos. Nesses locais, temos as seguintes condições: T ≃
4000 K (temperatura do gás), B ≃ 0,1 T e o número de partı́culas, por unidade de volume, vale
N ≃ 1022 partı́culas/m3 .
(a) Considerando a equação de Clapeyron para gases ideais (P V = N kb T = nRT ), estime a pressão do gás numa mancha solar, e compare com a pressão atmosférica. kB = 1,38 × 10−23 J/K
(constante de Boltzmann).
(b) Admitindo que o gás é ideal e monoatômico, determine a densidade de energia térmica uT tı́pica
numa mancha solar.
(c) Determine a densidade de energia magnética u numa mancha solar.
(d) Determine a razão uT /u entre as densidades de energia térmica e magnética. Quando essa razão
é muito maior que 1, então o comportamento do gás é descrito basicamente por forças de pressão
termodinâmica, e se ela é muito menor que 1, então forças magnéticas é que são importantes.
Dentro de uma mancha solar, qual comportamento é exibido?
(e) Nas regiões longe das manchas solares, os dados tı́picos são T ≃ 6000 K, N ≃ 1022 partı́culas/m3
e B ≃ 10−4 T. Nesse caso, quais forças são relevantes?
4
11. Considere que voltı́metros ideais meçam o valor da integral
Z
b
E~ · d~ℓ
(1)
a
efetuada ao longo de seus terminais, utilizando uma curva C que passa por dentro do voltı́metro e que
coincide com seus contatos. Além disso, considere que num resistor, a relação entre corrente, resistência
e a integral de linha de E~ é
1
I=
R
Z
Q
E~ · d~ℓ
(2)
P
onde a integração é feita no mesmo sentido que a corrente passa pelo resistor, e o caminho de integração passa por dentro do resistor. Assim, na equação (2), os termos são tais que a corrente entra no
resistor por P e sai por Q.
Suponha agora que temos uma configuração como a mostrada na figura abaixo. Há um solenoide muito
longo, e uma corrente I que varia linearmente com o tempo percorre o solenoide, como indicado. Há
um fluxo magnético variável dado por ΦB = αt, com α > 0 e com o sentido positivo orientado para
dentro do plano da figura. Dois voltı́metros ideiais e dois resistores ideais são conectados como na
figura. Quais são as leituras V1 e V2 indicadas pelos voltı́metros, considerando os terminais na forma
indicada na figura, e a equação (1)?
B
I
b
V1
a
b
R1
solenóide
A
5
R2
V2
a