Faculdades Integradas Campos Salles

Faculdades Integradas Campos Salles
Aula 5 – FUNÇÃO DE 2º GRAU ( ou função quadrática )
Dados três números reais, a, b e c, com a 0 , denominamos função de 2º grau ou função
quadrática à função f(x) = a x 2 + bx + c , definida para todo número real x.
Exemplos:
a) f(x) = 2 x 2  3x + 4
2
b) f(x) =  x + x  5
2
c) f(x) = 4 x + 10
2
d) f(x) = x  6x
2
e) f(x) =  x 2
9
onde
a=2
,
b = 3
e
c=4
onde
a = 1
,
b=1
e
c = 5
onde
a = 4
,
b=0
e
c = 10
onde
a=1
,
b = 6
e
c=0
onde
2
a=
9
,
b=0
e
c=0
A curva que representa graficamente a função de 2º grau é denominada parábola.
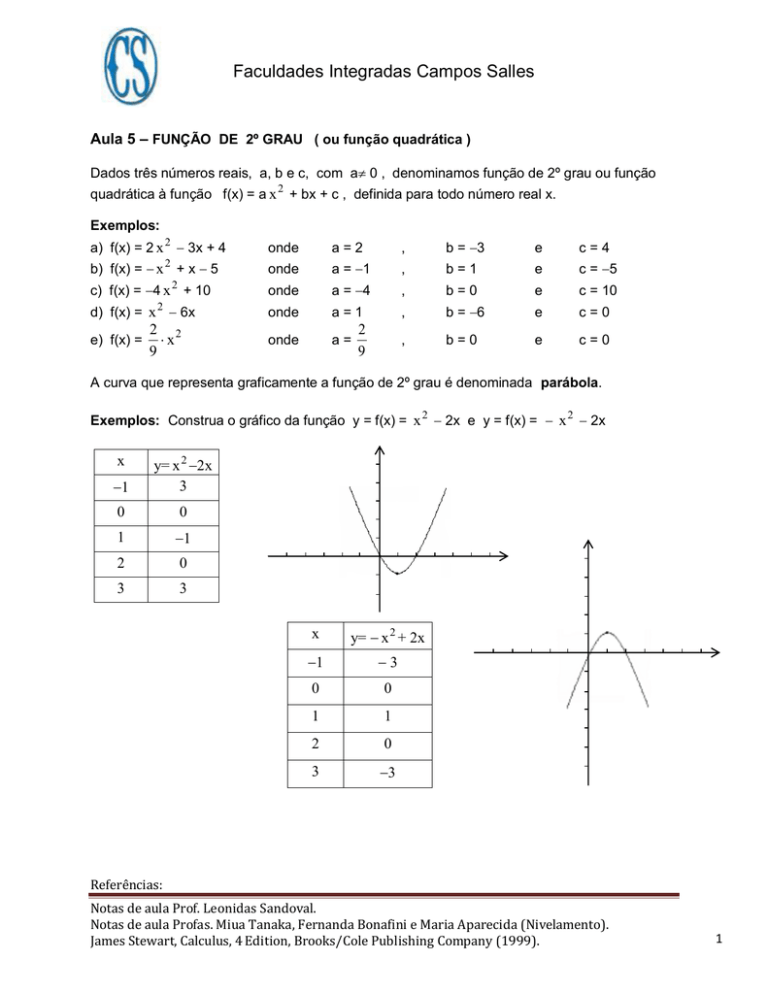
Exemplos: Construa o gráfico da função y = f(x) = x 2  2x e y = f(x) =  x 2  2x
1
y= x 2 2x
3
0
0
1
1
2
0
3
3
x
x
y=  x 2 + 2x
1
3
0
0
1
1
2
0
3
3
Referências:
Notas de aula Prof. Leonidas Sandoval.
Notas de aula Profas. Miua Tanaka, Fernanda Bonafini e Maria Aparecida (Nivelamento).
James Stewart, Calculus, 4 Edition, Brooks/Cole Publishing Company (1999).
1
Faculdades Integradas Campos Salles
 Concavidade
A parábola que representa uma função quadrática pode ter a concavidade voltada para “cima”
ou voltada para “baixo”. A concavidade é “voltada para cima” quando a > 0 e é “voltada
para baixo” quando a < 0.
Assim, considerando a função quadrática y = a x 2 + bx + c , podem ocorrer dois casos:
a>0
a<0
 Zeros (ou Raízes) da Função Quadrática
Os valores de x para os quais a função de 2º grau f(x) = a x 2 + bx + c se anula, isto é, f(x) = 0
denominam-se zeros ou raízes da função. Achar os zeros da função quadrática equivale a
resolver a equação de 2º grau:
a x 2 + bx + c = 0
Podemos interpretar geometricamente os zeros da função de 2º grau, como sendo as
abscissas dos pontos em que a parábola y = a x 2 + bx + c corta o eixo x.
y
x
0
raiz
raiz
Exemplos: Determine os zeros da função f(x) = 2 x 2  5x  3.
f(x) = 0
2 x 2  5x  3 = 0
  b2  4ac 
 5 2  4  2   3
 25  24  49
Referências:
Notas de aula Prof. Leonidas Sandoval.
Notas de aula Profas. Miua Tanaka, Fernanda Bonafini e Maria Aparecida (Nivelamento).
James Stewart, Calculus, 4 Edition, Brooks/Cole Publishing Company (1999).
2
Faculdades Integradas Campos Salles
b  
x =
2a

  5  49
22
57

4
x1  3


1
x 2   2
A existência dos zeros reais de uma função de 2º grau depende do sinal de . Temos três
casos a considerar:
 > 0: nesse caso, a equação tem duas raízes reais e a parábola intercepta o eixo x em dois
pontos;
 = 0: nesse caso, a equação tem uma raiz real e a parábola intercepta o eixo x em apenas um
ponto;
 < 0: nesse caso, a equação não tem nenhuma raiz real e a parábola não intercepta o eixo x.
Já vimos que o gráfico da função do 2º grau pode ter concavidade voltada para cima ou para
baixo. Esse fato está relacionado ao sinal do coeficiente de x 2: a. Observamos também, que a
ordenada do ponto onde a parábola intercepta o eixo y pode ser obtida diretamente da
expressão da função: é o termo independente c.
Podemos, então, organizar os seguintes gráficos:
< 0
y
y
y
= 0
> 0
S
S
S
o
a> 0
o
a> 0
a> 0
o
x1
V
x2
x
0
0
V
x
0
x
V
Referências:
Notas de aula Prof. Leonidas Sandoval.
Notas de aula Profas. Miua Tanaka, Fernanda Bonafini e Maria Aparecida (Nivelamento).
James Stewart, Calculus, 4 Edition, Brooks/Cole Publishing Company (1999).
3
Faculdades Integradas Campos Salles
Valor Máximo e Valor Mínimo da Função do 2º Grau
Examinando os gráficos abaixo, observamos que:
Se a > 0, então para x = - b/2a a função tem o seu valor mínimo dado por
y
a> 0
xv
x
0
yv
V
yv = f (- b/2a) = - /4a.
Se a < 0, então para x = - b/2a a função tem o seu valor máximo dado por:
y
yv
0
a< 0
V
xv
x
yv = f (- b/2a) = - /4a.
 Estudo do Sinal
O estudo do sinal da função é feito analisando-se o esboço do gráfico.
Exemplos:
Referências:
Notas de aula Prof. Leonidas Sandoval.
Notas de aula Profas. Miua Tanaka, Fernanda Bonafini e Maria Aparecida (Nivelamento).
James Stewart, Calculus, 4 Edition, Brooks/Cole Publishing Company (1999).
4
Faculdades Integradas Campos Salles
Estudar o sinal das seguintes funções do 2º grau:
a) y = 3x2 - 4x + 1
Para encontrarmos os zeros da função devemos fazer y = 0. Dessa forma obtemos a equação:
3x2 - 4x + 1 = 0.
b 
, vamos resolver a equação.
2a
 = (- 4)2 – 4 . 3 . 1 = 16 – 12 = 4    2
 (4)  2 4  2
1
x

 x1 
e x2  1
2(3)
6
3
Lembrando que  = b2 – 4ac e x 
A parábola corta o eixo x nos pontos de abscissas 1/3 e 1. Como a = 3 > 0, sua concavidade
está voltada para cima.
+
+
1
3
-
1
x
Estudo do Sinal: Examinando o esboço do gráfico podemos afirmar que:
para x < 1/3 ou x > 1  y > 0;
para x = 1/3 ou x = 1  y = 0;
para 1/3 < x < 1  y < 0.
b) f(x) = - x2 + 6x - 9
Os zeros da função são calculados resolvendo-se a equação - x2 + 6x – 9 = 0.
 = 62 – 4 . (-1) . (-9) = 36 – 36 = 0
x = - 6/ 2(-1) = - 6/-2 = 3
A parábola tangencia o eixo x no ponto de abscissa 3; como a = -1 < 0, sua concavidade está
voltada para baixo.
Referências:
Notas de aula Prof. Leonidas Sandoval.
Notas de aula Profas. Miua Tanaka, Fernanda Bonafini e Maria Aparecida (Nivelamento).
James Stewart, Calculus, 4 Edition, Brooks/Cole Publishing Company (1999).
5
Faculdades Integradas Campos Salles
3
x
-
Estudo do Sinal:
-
para x  3  y < 0.
para x = 3  y = 0.
c) y = x2 + 2x + 3
Os zeros da função são calculados resolvendo-se a equação x2 + 2x + 3 = 0.
 = 22 – 4 . 1 . 3 = 4 – 12 = - 8
A equação não possui raízes reais.
A parábola não corta nem tangencia o eixo x. Como a = 1 > 0, sua concavidade está voltada
para cima.
+
Estudo do Sinal
x  R  y > 0.
+
x
Referências:
Notas de aula Prof. Leonidas Sandoval.
Notas de aula Profas. Miua Tanaka, Fernanda Bonafini e Maria Aparecida (Nivelamento).
James Stewart, Calculus, 4 Edition, Brooks/Cole Publishing Company (1999).
6