Teorema do Transporte de Reynolds

Mecânica dos Fluidos - Professor Eduardo Loureiro
Hidrodinâmica
FORMA INTEGRAL DA EQUAÇÃO DA CONTINUIDADE (CONSERVAÇÃO DE MASSA):
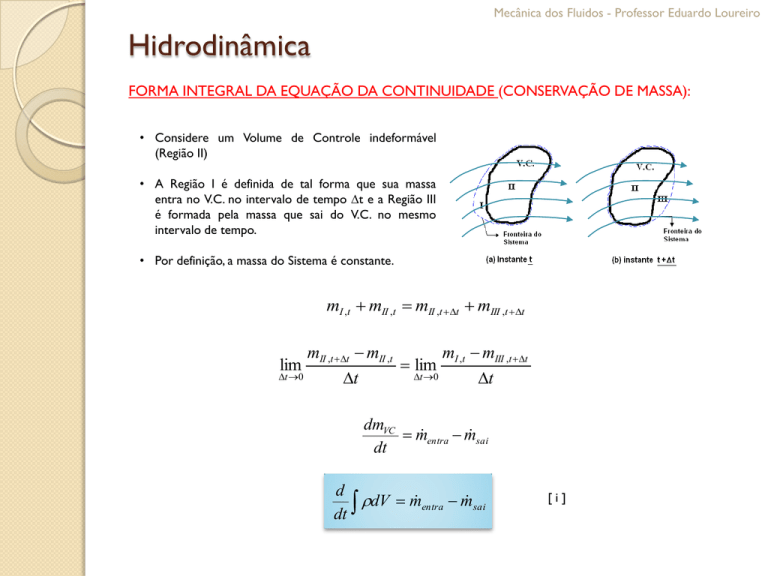
• Considere um Volume de Controle indeformável
(Região II)
• A Região I é definida de tal forma que sua massa
entra no V.C. no intervalo de tempo t e a Região III
é formada pela massa que sai do V.C. no mesmo
intervalo de tempo.
• Por definição, a massa do Sistema é constante.
mI ,t  mII ,t  mII ,t  t  mIII ,t  t
lim
t 0
mII ,t  t  mII ,t
t
 lim
t 0
mI ,t  mIII ,t  t
t
dmVC
 m entra  m sai
dt
d
dV  m entra  m sai
dt 
[i]
Mecânica dos Fluidos - Professor Eduardo Loureiro
Hidrodinâmica
FORMA INTEGRAL DA EQUAÇÃO DA CONTINUIDADE (CONSERVAÇÃO DE MASSA):
Quando queremos determinar a vazão em volume (Q [m3/s])
de um escoamento pelo interior de um tubo, basta que
multipliquemos a velocidade média do fluido pela área de
seção do tubo:
 m3 
m
2
Q  V    A m  Q 
s
 s 
 
No caso de um tubo, o escoamento é sempre perpendicular
à área de seção do mesmo.
Imaginemos agora uma pequena área diferencial, dA, circular,
na superfície de controle:
A vazão normal à superfície é dada por:


VN dA ou V  dA

dA é definido como o vetor normal à superfície com módulo
igual à área diferencial dA e sempre apontando para fora do
volume de controle.
Mecânica dos Fluidos - Professor Eduardo Loureiro
Hidrodinâmica
FORMA INTEGRAL DA EQUAÇÃO DA CONTINUIDADE (CONSERVAÇÃO DE MASSA):
Então:
m entra  
 V cos dA
A.entrada
pois, o cos, quando o escoamento é para o interior da
Superfície de controle, será sempre negativo ( > 90º).
m sai 
 V cos dA
A. saida
Pois, neste caso, o cos é sempre positivo.
Voltando à equação
d
dV  m entra  m sai
dt 
[i]:
d
d    V cos dA   V cos dA
dt V.C .
A.entrada
A. saida
Chegamos à forma integral da Equação da Continuidade:
 
d

d




V
S .C  dA
dt V.C
Se o escoamento for PERMANENTE,
a massa total dentro do V.C. é
constante e independe do tempo,
portanto:
 entra  m
 sai
m
Mecânica dos Fluidos - Professor Eduardo Loureiro
Hidrodinâmica
FORMA INTEGRAL DA EQUAÇÃO DA CONTINUIDADE (CONSERVAÇÃO DE MASSA):
EXERCÍCIO:
Um fluido incompressível escoa de modo permanente através do duto
com duas saídas. O perfil de velocidades é reto nas seções 1 e 2,
porém é parabólico na seção 3. Calcule a velocidade V1.
Dados:
A1= 3ft2;
A2= 2 ft2;
A3=1ft2;
V2=1ft/s
2
 r  ft
V3  41  2 
 R  s


 V  dA  0
Escoamento permanente:
S .C












0   
2

 V  dA   V  dA   V  dA   V  dA   V  dA  0
S .C
1
2
3
4
 
 
 
V

d
A

V

d
A

V


  dA  0
1
2
3
 
      V  dA  V1 A1  3V1
1


  0   V  dA  V2 A2  2
2
 
V
  dA   V3 2rdr
3
r
3
R
dA
 3V1  2  2R 2  0
dr
4 ft
V1 
3 s
R
  R  r2 

r3 
2



3 V  dA  0 41  R 2 2rdr  8 0  r  R 2 dr  2R
Mecânica dos Fluidos - Professor Eduardo Loureiro
Hidrodinâmica
Relembrando, quando estudamos a dinâmica de corpos rígidos:

 dV
a
dt


F  ma


P  mV
 

 d mV
F
dt
É O MOMENTO (OU QUANTIDADE DE MOVIMENTO).
TEOREMA DO TRANSPORTE DE REYNOLDS:
Seja N, a magnitude de uma propriedade física presente em um meio material
 contínuo. Se esta propriedade está
sendo transportada pela ação do escoamento do material, com velocidade V , então, o Teorema do Transporte de
Reynolds afirma que a taxa de variação com o tempo da quantidade total de N é igual às variações instantâneas de N no
interior do volume de controle, somadas à integral (em toda a superfície de controle) da taxa na qual N está sendo
transportada através da superfície de e para a vizinhança.
dN
dt


sistema
 


d



V

SC  dA
t VC
é a propriedade intensiva, correspondente a N, igual a N por unidade de massa.
Mecânica dos Fluidos - Professor Eduardo Loureiro
Hidrodinâmica
Se considerarmos a massa, M, como sendo a propriedade N. Então teremos:
N M
dM
dt
0
sistema

M
1
M
Aplicando o Teorema do Transporte de Reynolds:
dN
dt
 

 d  V  dA
t VC
sistema
SC
 

0
d   V  dA

t VC
SC
 
d
d    V  dA

dt V .C
S .C
Que é a forma integral da Equação da Continuidade (conservação de massa)!
Mecânica dos Fluidos - Professor Eduardo Loureiro
Hidrodinâmica


Se considerarmos o momento, P  mV , como sendo a propriedade N. Então teremos:


N  P  mV


dP
F
dt sistema

mV 

V
m
Aplicando o Teorema do Transporte de Reynolds:
dN
dt
 

 d  V  dA
t VC
sistema
SC
  
  
F   Vd   VV  dA
t VC
SC
Lembrado-nos que:
AV  m
Mecânica dos Fluidos - Professor Eduardo Loureiro
Hidrodinâmica
Consideremos o Volume de Controle ao lado, que tem uma entrada
(seção (1)) e uma saída (seção (2)). O escoamento transmite momento
para dentro e para fora do V.C.
Em regime permanente, a força resultante que atua sobre o V.C. é igual
à diferença entre as taxas de momento saindo e entrando no V.C. que
acompanham o fluxo de massa.
0 (escoamento permanente)
  
  
F   Vd   VV  dA
t VC
SC




 
 V2  m
 V1  m
 V2  V1
F m

1  m
2
Em regime permanente: m
A Equação do Momento é uma equação vetorial. As componentes x, y e
z de F são Fx, Fy e Fz. As componentes da velocidade são u, v e w. A vazão
mássica (em massa) é dada por:
  AV
m
Mecânica dos Fluidos - Professor Eduardo Loureiro
Hidrodinâmica
EXEMPLO:
Um jato de água sai de um bocal com velocidade uniforme V = 3,05 m/s, atinge a superfície plana de um defletor e é
desviado em um ângulo . Determine a força de ancoragem necessária para manter o defletor parado, em função
de .
HIPÓTESES:
Regime permanente;
Água é incompressível ( = 1000 kg/m3);
A pressão é a atmosférica em todo o V.C.
Para o V.C. do lado direito da figura, as componentes x e y da equação do momento ficam:
F
X
 u 2  u1 
m
F
Y
 v2  v1 
m
Mecânica dos Fluidos - Professor Eduardo Loureiro
Hidrodinâmica
EXEMPLO:
Uma vez que a pressão é a atmosférica em toda a superfície de controle, a força total líquida de pressão é nula.
Então o somatório de forças em cada eixo x e y se resume às forças de ancoragem FAX e FAY:
 V cos   V   m
 V 1  cos  
FAX  m
 Vsen  0  m
 Vsen
FAY  m
Como m
    A V
FAX   AV 2 1  cos  
FAY  AV 2 sen
Substituindo os valores:



FAX  1000 5,6  10 3 3,052 1  cos    52,11  cos  N 
FAY  52,1sen N 
O sinal negativo de FAX indica que a componente horizontal da força de ancoragem é exercida para a esquerda.
Mecânica dos Fluidos - Professor Eduardo Loureiro
Hidrodinâmica
EXEMPLO:



FAX  1000 5,6  10 3 3,052 1  cos    52,11  cos  N 
Se  = 90º, as forças seriam:
FAX = - 52,1N e FAY = 52,1N
Assim, conforme a figura, a força de ancoragem deve se opor ao momento
do fluido entrando no V.C. e fornecer o momento de saída.
Já se  = 180º, o jato retorna e as forças serão:
FAX = -104,2N e FAY = 0
FAY  52,1sen N 