Diagonais de um polígono convexo - 8º Ano

DISCIPLINA:
8º
SÉRIE:
ASSUNTO:
ALUNO:
Matemática
TURMA:
Diagonais de um Polígono Convexo
PROFESSOR:
Saulo Viana
Matutino
TURNO:
BIMESTRE: IV
DATA:
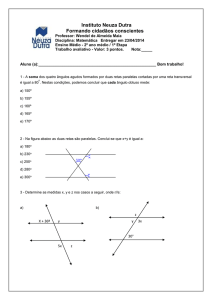
Relembrando
Denominamos polígono uma figura formada por segmentos de reta que delimitam uma região. Os polígonos precisam ser
figuras fechadas. Observe:
Os polígonos possuem os seguintes elementos: vértices, lados, ângulos internos, ângulos externos e diagonais. Dos
elementos citados vamos estudar o significado de diagonais e como calcular o número de diagonais de um polígono
qualquer.
Denominamos por diagonal o segmento de reta que une um vértice ao outro. O número de diagonais de um polígono é
proporcional ao número de lados.
Note que na figura A temos quatro vértices, então traçamos quatro diagonais, cada uma partindo de um vértice. Mas
observe que a diagonal PR é a mesma RP, e a diagonal SQ é a mesma QS, então sempre dividiremos o número de
diagonais por 2. Para cálculos envolvendo o número de diagonais, utilizamos a seguinte fórmula:
A fórmula n indica o número de lados e n – 3 determinam o número de diagonais que partem de um único vértice e a divisão
por dois elimina a duplicidade de diagonais ocorridas em um polígono.
Exercício.
01
Questão:
A soma dos ângulos internos de um polígono regular de n lados é 2340º. Determine o número de diagonais deste
polígono.
02
Questão:
Determine o número de diagonais de um polígono cuja soma dos ângulos internos é 3600°.
03
Questão:
Determine nome do polígono em que a quantidade de diagonais é igual ao triplo do número de lados?
(Obs: Dados do problema: d = 3n).
04
Questão:
Qual o número de diagonais de um polígono com 15 lados?
05
Questão:
Em um polígono o número de diagonais é igual ao quádruplo do número de lados. Quantos lados e diagonais possui o
polígono? (Obs: Use d = 4n).
.
06
Questão:
Quantos lados possui o polígono onde o número de lados corresponde a sexta parte do número de diagonais?
𝑑
(Obs: Use n = ).
6