Olimpíada SAS – 1ª serie-Física-2016

O LIMPÍADA DE
FÍSICA
Resoluções
01 B
Para o sistema vetorial citado na questão, tem-se o
seguinte:

b
60 km

a
  
a+b+c = 0

S=0
Invertendo qualquer um dos vetores, tem-se a seguinte
situação:
Escrevendo as funções horárias dos dois movimentos
retrógrados, tem-se:
Aplicando o Teorema de Pitágoras:
d2 = SA2 + SB2

a
352 = (80 – 6t)2 + (60 – 8t)2
1 225 = 6 400 – 960t + 36t2 + 3 600 – 960t + 64t2
1 225 = 10 000 – 1 920t + 100t2
100t2 – 1 920t + 8 775 = 0
20t2 – 384t + 1 755 = 0
∆ = 147 456 – 140 400
∆ = 7 056
02 E
Logo:
O carro O inicia a viagem 3 horas após a partida do
carro C. Assim, em um gráfico no qual a abscissa está
associada ao instante t, os instantes de partidas serão
distintos, com um intervalo de 3 horas. Além disso, a
velocidade de O é maior que a velocidade de C, ambas
constantes. Desse modo, em um gráfico da posição pelo
tempo, a inclinação da reta deve ser maior para o carro
O (velocidade maior).
Portanto, o gráfico que contém as características cinemáticas citadas é o da alternativa E.
De acordo com o enunciado do problema, para a ida,
após 10 horas de movimento, tem-se o seguinte:
04 D
a) (F)Note que, entre 0 e t1, o movimento é retardado e
o móvel freia. A partir de t2, o movimento é acelerado e o móvel muda de sentido.
b) (F) Observe o comentário da alternativa anterior.
c) (F)Nessa situação, do lançamento até o repouso instantâneo, a velocidade tem valor positivo, ou seja,
de 0 a t1, v > 0. No retorno, o movimento é retrógrado, caracterizando valores negativos de velocidade.
d)(V)
Como a trajetória está orientada para baixo,
durante a subida, há um movimento retrógrado
(v < 0) e, durante a descida, um movimento progressivo (v > 0).
e) (F)Para essa situação, a velocidade no instante t = 0
deve ser nula, o mesmo ocorre no instante t = t2, o
que não acontece na análise do gráfico.
14444244443
vB = 0

vB
B

vA
vA = 8 km/h
vB = 6 km/h
vA = 0
A
14444444244444443
80 km
384 ± 7056 384 ± 84
=
2 · 20
40
300
t' =
⇒ t' = 7,5 h (antes da origem)
40
468
t" =
⇒ t" = 11,7 h (depois da origem)
40
t=
03 D
O
A
14444444244444443
80 km
SB = 60 – 8t

S ⇒ vetor soma
Ao inverter qualquer um dos vetores, não haverá mais um
polígono fechado, uma vez que o módulo do vetor soma

(S) não será mais nulo, ou seja, será sempre diferente de
zero.
60 km

vA
SA = 80 – 6t

b
d
vA' = 6 km/h
vB' = 8 km/h

S
B

vB
O

c
14444244443

c
Após a inversão dos movimentos, os módulos das velocidades foram trocados. Desse modo:
1a Série – Ensino Médio
1
OLIMPÍADA DE
FÍSICA
07 C
1
a1 = –2 cm/s2
v0 = –6 cm/s
2
Para solucionar esse problema, é muito útil lembrar da
sequência de Galileu, a qual afirma que, para qualquer
movimento com aceleração constante e com velocidade
inicial nula, há, para iguais intervalos de tempo:
a2 = 1 cm/s2
d
As funções horárias das posições 1 e 2 dos móveis podem
ser escritas como:
3d
2t 2
S1 = 0 + 2t –
⇒ S1 = 2t – t2
2
5d
t2
2
É possível representar essas funções por meio de um gráfico da posição em função do tempo.
S2 = b – 6t +
7d
S (cm)
b
S1
E
SE
S2
344244134241321321
05 C
Orientando uma trajetória para a direita:
v0 = 2 cm/s
∆t
∆t
∆t
∆t
O problema pede as distâncias associadas a um intervalo
de tempo igual a 1 s (intervalos iguais).
Para que a condição seja satisfeita, tem-se:
x4 = 7x1
tE
t (s)
No ponto E, os dois móveis estão no ponto de retorno,
em que a velocidade de ambos é nula. Como a posição
de encontro é a ordenada que corresponde aos vértices
das parábolas, tem-se:
x3 = 5x1
x 2 = 3x1
x1
ƒƒ S1 = 2t – t2
∆=4
SE =
Portanto:
ƒƒ x1 = 5
ƒƒ x2 = 3 · x1 = 15
ƒƒ x3 = 5 · x1 = 25
ƒƒ x4 = 7 · x1 = 35
−∆
−4
=1
=
4 · ( −1) −4
2
ƒƒ S2 = b – 6t + t
2
∆ = 36 – 2b
−∆
−36 + 2b
SE =
=
1
2
4·
2
Logo:
−36 + 2b
=1
2
–36 + 2b = 2
2b = 38 ⇒ b = 19 cm
08 C
v0 = 0 →
a
d
06 A
No primeiro trecho, a velocidade é constante, pois o gráfico da posição pelo tempo (S · t) é uma reta.
No segundo trecho, a posição da bicicleta permanece a
mesma, caracterizando repouso (velocidade nula).
No terceiro trecho, há um movimento uniformemente
variado com aceleração negativa, pois o arco de parábola
está com a concavidade voltada para cima. A velocidade
nesse trecho também é negativa, pois as posições decrescem. Desse modo, o movimento é uniformemente acelerado.
No último trecho, há um movimento uniformemente
variado com aceleração positiva, pois o arco de parábola
está com a concavidade voltada para baixo. A velocidade
nesse trecho é negativa, pois as posições decrescem.
Logo, o movimento é retardado.
Ao final do movimento, o deslocamento da bicicleta será
nulo, pois ela retorna para a mesma posição do início.
2
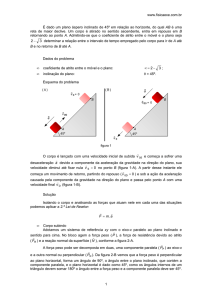
De acordo com o enunciado do problema, o corpo sempre estará alinhado verticalmente com o ponto A quando
abandonado no plano inclinado.
θ
A
cos θ =
x
O
x
⇒ x = d · cos θ
d
A distância OA = x é sempre a mesma para o ângulo de
inclinação.
Sabe-se que a aceleração do corpo, ao longo do plano
inclinado, é uma componente da aceleração da gravidade
(g), dada por:
a = g · sen θ
O corpo parte do repouso (v0 = 0) e realiza um movimento
uniformemente variado ao longo do plano. Logo:
1a Série – Ensino Médio
d=
a · t 2 g · sen θ 2
=
·t
2
2
O LIMPÍADA DE
FÍSICA
Desse modo, é possível escrever:
g · sen θ · cos θ 2
x=
·t
2
g · 2 · sen θ · cos θ 2
·t
x=
4
g · sen (2θ ) 2
·t
x=
4
4x
t2 =
g · sen 2θ
t=2
12 B
É possível distribuir a massa dessa corrente em duas parcelas:
ƒƒ mH – massa sobre a superfície horizontal;
ƒƒ mx – massa pendurada.
Considerando que as massas são conectadas, tem-se a
seguinte relação:
L
x
x
g · sen 2θ
Como g e x são fixos, o tempo será mínimo quando
sen (2θ) for máximo. Logo:
sen (2θ) = 1
2θ = 90º
θ = 45º
09 C
A velocidade angular (ω) dos dois cilindros é a mesma,
pois eles são coaxiais (possuem o mesmo eixo).
Sabe-se que v = w · K, em que v é a velocidade linear de
um ponto na periferia de um cilindro girante.
Como K > r, a velocidade linear do bloco A é maior que a
velocidade linear do bloco B. Portanto, o bloco A alcançará S2 antes do bloco B.
10 B
De acordo com o enunciado do problema, tem-se:
ω1
A
Instante t + 2
mx
x
= MT · L ⇒ mx = MT ·
x
L
Aplicando a 2a Lei de Newton para o sistema, tem-se:
Px = (mH + mx) · a
mx · g = MT · a
MT · x · g = MT · a
L
x
a=g·
L
Note que, enquanto existir mH, a aceleração aumenta
linearmente com o comprimento da parte pendurada.
Desse modo, a aceleração é crescente até x = L, em que
a corrente estará totalmente na vertical, caracterizando
uma queda livre.
NC
PC
fat
No encontro, as posições angulares são iguais. Logo:
ϕ1 = ϕ2
ω1 · (t + 2) = ω2 · t ⇒ 2 · (t + 2) = 6t ⇒ 2t + 4 = 6t ⇒ t = 1,0 s

at
P

v
Logo, a aceleração resultante terá a seguinte orientação:

at

aR
P

ar
a
C
2
11 D
As hélices do ventilador executam uma trajetória circular,
permitindo a existência de uma aceleração radial (aceleração centrípeta) associada para essa notação.
Por outro lado, as hélices do ventilador estão sofrendo
uma desaceleração, ou seja, existe uma aceleração tangencial que se opõe à velocidade instantânea das hélices.
L é o comprimento total da corrente.
Como a corrente é homogênea, a densidade linear (massa
por unidade de comprimento) é constante. Logo:
13 D
Quando o carro acelera, as rodas com tração motora
empurram o bloco A para trás, por meio de uma força de
atrito estático entre os pneus e a superfície de A. Desse
modo, isolando os blocos com as respectivas forças
atuantes, tem-se a seguinte representação:
ω2 Instante t

ar
mx
Adotando o ponto A como origem da trajetória circular,
tem-se:
ƒƒ ϕ1 = ϕ0 + ω1 · t' = 0 + ω1 · (t + 2)
1
ϕ1 = ω1 · (t + 2)
ƒƒ ϕ2 = ϕ0 + ω2 · t = 0 + ω2 · t = ω2 · t
x
mH
NC
NA
fat
T
A
PA
fat(A,S)
fat ⇒ força de atrito entre os pneus do carro e o bloco A.
fat(A,S) ⇒ força de atrito dinâmico entre A e a superfície
horizontal.
T
B
PB
Os blocos A e B devem ficar em repouso. Portanto:
T = PB = mg
T + fat(A,S) = fat
T + μ · nA = fat
T + μ (PA + NC) = fat
mg + μ (PA + PC) = fat
mg + μ · (mg + mg) = fat
mg(1 + 2 μ) = fat
Aplicando a 2a Lei de Newton para o carro, tem-se:
fat = FR = m · a
mg · (1 + 2 μ) = m · a
a = g(1 + 2 μ)
1a Série – Ensino Médio
3
OLIMPÍADA DE
FÍSICA
14 C
Identificando todas as forças no sistema apresentado:
16 B
O gráfico mostra como a aceleração varia com a distância.
A área sob o gráfico dará o produto a · x, em que x é a
distância percorrida.
Entre 0 e 8 m, a área é correspondente a uma semicircunferência de raio igual a 4. Logo:
π ⋅ 42
A0; 8 m =
= 8π
2
a · x0; 8 m = 8π m2/s2
Entre 8 m e 12 m, a área corresponde a uma semicircunferência de raio 2. Logo:
π · 22
= 2π
2
a · x8 m; 12 m = (–2π) m2/s2 (semieixo negativo)
Durante todo o trajeto, o produto a · x vale:
a · x = 8π + (–2π) = 6π m2/s2
Sabe-se que o trabalho procurado é dado por:
⋅ a ⋅ x = 1 · 6π
τ=F·d=m
T2
T2
T2
T2
T2
NH
T1
T2
T1
NH
PH
PP
Considerando que a pessoa pode puxar o sistema em
equilíbrio dinâmico (velocidade constante), tem-se:
ƒƒ 2T2 = T1
ƒƒ NH + T2 = PH (para a pessoa)
ƒƒ NH + PP = T1 (para a prancha)
Na situação limite, para que a pessoa puxe a prancha, a
força normal entre ela e a plataforma deve tender a zero.
2T2 = T1
PP = T1
Dessa forma:
2T2 = T1
2PH = PP
2mH · g = mP · g
2 · 75 = mP ⇒ mp = 150 kg
15 D
O caixote realiza um movimento retilíneo uniforme, ou
seja, não há variação da energia cinética nele. Logo, o trabalho feito pela força de tração (T) deve ser, em módulo,
igual ao trabalho feito pela força de atrito (fat), a qual varia
com a massa de areia perdida.
Como a perda de areia é de 1 kg/m, ao final de 1 000 m, o
caixote não terá mais areia (perda de 1 000 kg), restando
apenas sua massa.
A força de atrito entre o caixote e o solo vale:
fat = μ · Nsistema
fat = μ · (Pcaixote + Pareia)
fat = μ · g · (mcaixote + mareia),
em que mareia é variável e diminui linearmente com a distância percorrida.
A seguir está representado um gráfico da força de atrito
pela distância percorrida.
fat (N)
fati
fatf
0
L = 1 000
fati = μ · g (mcaixote + mi,areia)
fati = 0,3 · 10 · 2 000
fati = 6 000 N
fatf = μ · g · mcaixote = 0,3 · 10 · 1 000
fatf = 3 000 N
A área sob a reta é numericamente igual ao módulo do
trabalho da força de atrito.
A = ( fati + fat f ) ⋅ L = ( 6000 + 3000 ) ⋅ 1000
2
2
A = 4,5 · 106
|τat| = 4,5 · 106 J
τT = 4,5 · 106 J
4
A8 m; 12 m =
τ = 6π J
6π
17 E
No instante t = 4 s, as três forças possuem o mesmo
módulo.
No sistema vetorial de forças mostrado, cada ângulo vale
120o, pois eles são iguais.
Na figura A, três vetores têm a mesma origem e formam
um ângulo de 120o entre um vetor e outro consecutivo,
originando, portanto, um vetor resultante nulo, igual a
zero.
18 B
Ao observar o sistema lateralmente, note que:
N
P·
θ
sen
θ
P·
co
sθ
P
Note que a força responsável pela trajetória oblíqua é a
componente do peso, P · sen θ. Logo:
FR = P · sen θ
m · a = m · g · sen θ
a = g · sen θ
a = 10 · sen 30o
a = 5 m/s2
A aceleração de 5 m/s2 faz o módulo vertical da velocidade variar no movimento, sendo paralela à superfície do
plano inclinado.
A equação de alcance horizontal em um lançamento oblíquo com ângulo α é dada por:
v 2 · sen (2α )
A= 0
a
Em que A = 5 m, v0 = 5 m/s e a = 5 m/s2.
25 · sen (2α )
5=
5
sen(2α) = 90o
α = 45o
1a Série – Ensino Médio
O LIMPÍADA DE
FÍSICA
19 B
De acordo com o enunciado do problema, tem-se a
seguinte situação:
A
y
β
B
α
v
v0
θ
O
C
x
Observando o polígono formado OABCO, o ângulo β é:
θ + 90° + β + 90° = 360°
θ + β = 180°
45º + β = 180°
β = 135°
Logo:
α + β = 180°
α + 135° = 180°
α = 45°
Na componente horizontal do movimento:
v0 = vx
x
v0 · cos θ = v · sen α
v0 · cos 45° = v · sen 45°
v = v0 (em módulo)
Assim, a velocidade final está associada ao ponto em que
a partícula toca o solo.
Logo, o tempo total do movimento é:
vy = v0 – g · t (trajetória orientada para cima)
y
–v · cos 45º = v0 · sen 45º – g · tT
g · tT = v0 · sen 45º + v0 · cos 45º
2
g · tT = 2 · v0 ·
2
v · 2
tT = 0
g
20 E
Quando C1 chega ao ponto B, a componente vertical da
sua velocidade é nula, e o mesmo ocorre com a velocidade inicial de C2 (em queda livre).
Em virtude da ação da aceleração da gravidade, os dois
sempre estarão na mesma linha horizontal em qualquer
instante. Desse modo, considerando o solo suficientemente grande, eles podem colidir entre si para qualquer
valor de d.
1a Série – Ensino Médio
5