Solução

www.fisicaexe.com.br
Um cilindro contendo n mols de um gás ideal sofre uma transformação adiabática.
a) Partindo da expressão W = p d V e usando a expressão p V  = constante , mostre que
o trabalho é dado por
∫
W =


1
−1
p i V i−p f V
f

b) Partindo da Primeira Lei da Termodinâmica na forma diferencial, prove que o trabalho
realizado também é dado por
W = n C V  T i−T f 
Mostre que este resultado coincide com o que foi obtido no item (a).
Esquema do problema
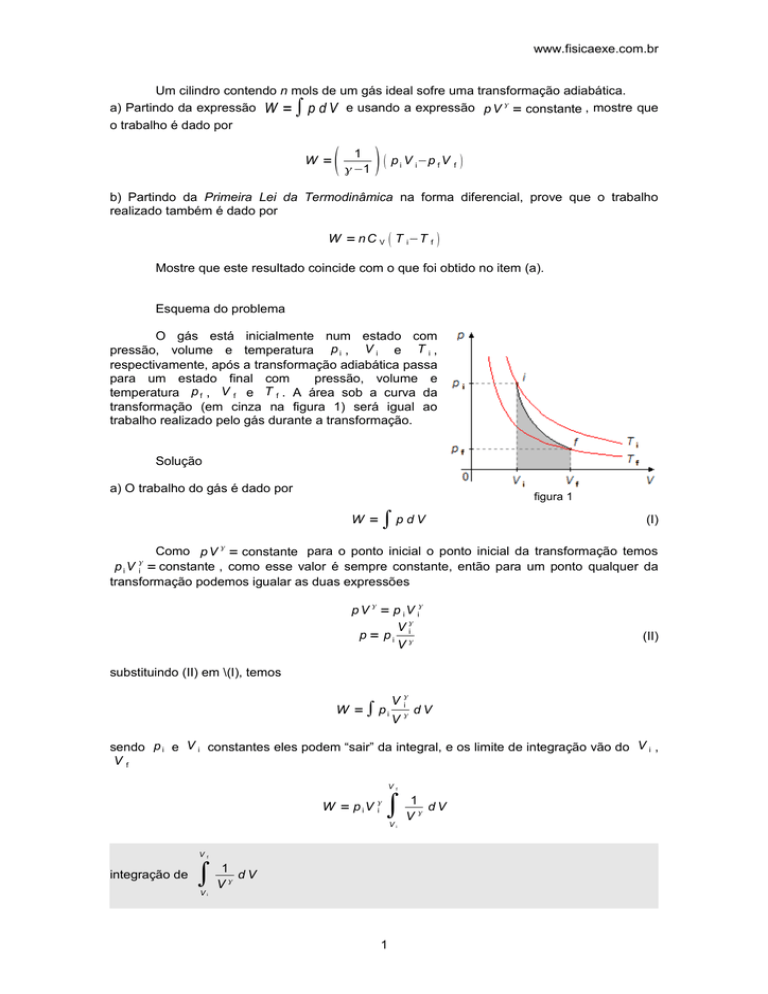
O gás está inicialmente num estado com
pressão, volume e temperatura p i , V i e T i ,
respectivamente, após a transformação adiabática passa
para um estado final com
pressão, volume e
temperatura p f , V f e T f . A área sob a curva da
transformação (em cinza na figura 1) será igual ao
trabalho realizado pelo gás durante a transformação.
Solução
a) O trabalho do gás é dado por
figura 1
W =
∫p dV
(I)
Como p V  = constante para o ponto inicial o ponto inicial da transformação temos
p i V = constante , como esse valor é sempre constante, então para um ponto qualquer da
transformação podemos igualar as duas expressões

i


p V = p iV i

V
p = p i i
V
(II)
substituindo (II) em \(I), temos
W =∫ pi
V
V

i

dV
sendo p i e V i constantes eles podem “sair” da integral, e os limite de integração vão do V i ,
Vf
V
W = p iV

i
f
∫ V1
Vi
V
integração de
f
∫ V1

dV
Vi
1

dV
www.fisicaexe.com.br
V
Vf
f
∫
Vi
1
dV =
V
∫
V
V
−
−1
V
−1
dV =
V
∣
f
=
V
i
V −1
V −1
V 1−−V 1−
f
i
− i
= f
−1 −1
1− 
i
1−

W = p iV i
W=

W=
W =


1
1−

1
1−
piV


i
p iV

 
1
1− 
W =
Vf

p iV i
1
1−
−V
1−
1−
i
1−
−V i 
 V 1−
f

i

V
V
Vf Vi
−
V f V i
f

f
−piV

i

i

f

Vi
V
p iV V f
−p iV i
V

i


(III)
Usando novamente a condição p V  = constante entre os pontos inicial e final da
transformação, obtemos

piV i = p f V

pV
pf = i  i
Vf

f
(IV)
substituindo (IV) em (III), temos




1
 p f V f −p i V i 
1− 
1
W =
 p f V f −p i V i 
− −1 
1
W =−
 p f V f− p i V i 
−1
W=

W =

1
−1


p i V i−p f V
f

b) Como a transformação é adiabática o calor trocado com o meio é nulo (Q = 0) e a Primeira
Lei da Termodinâmica se reduz a U = - W, que na forma diferencial é escrita como
d U = n C V d T = −p d V
onde C V é a Capacidade Térmica a Volume Constante e como d W = p d V podemos reescrever
−d W = n C V d T
d W = −n C V d T
integrando de ambos os lados da igualdade, temos
∫ d W ' = ∫ −n C
2
V
dT
www.fisicaexe.com.br
do lado esquerdo da igualdade os limites de integração vão de zero W, do lado direito da
igualdade o fator −n C V é constante e pode “sair” da integral, os limites de integração vão de
Ti a Tf
Observação: W' é a variável de integração, para não confundir com o valor superior da integral
W.
Tf
W
∫ d W ' = −n C ∫ d T
V
0
Ti
W
integração de
∫dW '
0
W
∫dW ' = W '∣
W
0
= W −0 = W
0
Tf
integração de
∫dT
Ti
Tf
∫dT = T ∣
Tf
Ti
= T f −T i
Ti
W = −n C V  T f −T i 
W = n C V  T i−T f 
Usando a Equação de Estado dos Gases Ideais ou Equação de Clapeyron escrevemos
esta equação para os estados inicial e final da transformação
p iV i = n R T i ⇒ T i =
p iV i
nR
e
pf V f = nR T f ⇒ T f =
pf V f
nR
(V)
onde R é a Constante Universal dos Gases Perfeitos, substituindo as duas expressões de (V)
no resultado acima, obtemos
W = nC V

p iV i p f V f
−
nR
nR

nC V
 p i V i−p f V f 
nR
CV
W =
 p i V i− p f V f 
R
W=
(VI)
Das expressões
C p −C V = R
e
=
Cp
CV
onde C p é a Capacidade Térmica a Pressão Constante, temos da segunda expressão
3
(VII)
www.fisicaexe.com.br
Cp = CV
substituindo na primeira expressão de (VII)
 C V −C V = R
C V  −1  = R
CV
1
=
R
−1
(VIII)
substituindo (VIII) em (VI), temos finalmente
W =

1
−1

p i V i−p f V
f

Q.E.D.
Observação: Q.E.D. é a abreviação da expressão em latim “quod erat demosntrandum” que
significa “como queríamos demonstrar”.
4