Multiplicação de números negativos

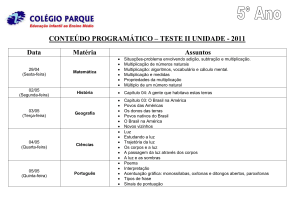
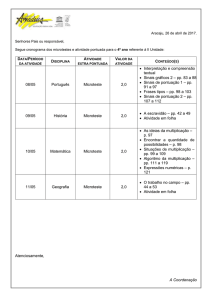
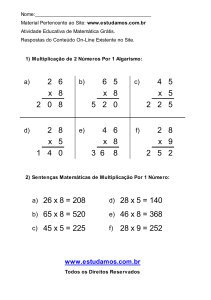
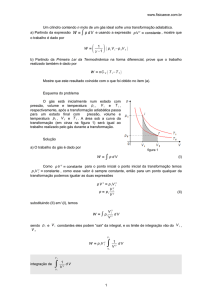
Multiplicação de números
negativos
Prof. Ilydio Pereira de Sá
UERJ / USS
Todos nós sabemos da grande dificuldade que os alunos do Ensino
Fundamental têm para o entendimento das operações matemáticas com
números negativos. Na passagem da adição para a multiplicação, quase
sempre, os alunos costumam confundir as regras de sinais dessas duas
operações.
A multiplicação de números negativos, na maioria das vezes, fica decorada
através de regrinhas que os alunos não conseguem entender.
Vamos aqui apresentar algumas formas significativas de abordagem do
tema em classes do Ensino Fundamental.
1) A partir das propriedades das igualdades e do conhecimento da
multiplicação de números de sinais contrários
a) Multiplicações do tipo -5 x 3 ou 4 x -6 são facilmente entendidas como
uma soma de quantidades negativas. O primeiro exemplo pode ser
observado como (-5) + (-5) + (-5), que o aluno já sabe ser igual a -15. O
segundo exemplo pode ser observado como (-6) + (-6) + (-6) +(-6), que ele
também sabe ser igual a -24.
Após o desenvolvimento de exemplos como os mostrados acima,
nossos alunos já podem inferir que o produto de um número positivo
por um número negativo será sempre um número negativo.
b) A partir do conhecimento do caso anterior, podemos formar alguma
seqüência de operações que acabe gerando o produto de duas
quantidades negativas, como vamos mostrar no exemplo abaixo:
(-4) x 4 = - 16
+4
(-4) x 3 = -12
+4
(-4) x 2 = - 8
+4
(-4) x 1 = - 4
(-4) x 0 = 0
+4
(-4) x (-1) = +4
+4
(-4) x (-2) = +8
+4
Verifique que, na seqüência formada, o
primeiro fator permaneceu constante (- 4),
enquanto que o segundo fator foi sempre
decrescendo uma unidade (4, 3, 2, 1, 0, - 1, ...).
Acreditamos que uma seqüência desse tipo
possa induzir que o produto de quantidades
negativas seja um número positivo.
Aconselhamos que demonstrações mais
rigorosas e abstratas sejam usadas em
momentos posteriores, para classes
mais
avançadas.
2) Justificativa de Cauchy
Pré-requisito: Conhecimento da reta dos inteiros, da noção de módulo e de
números simétricos ou opostos, com as respectivas notações.
1) a = +A
2) b = –A
3) +a = +A
4) +b = –A
5) –a = –A
6) –b = +A
Substituindo 1 em 3 temos:
+(+A) = +A
+.+=+
Substituindo 2 em 4 temos:
+(– A) = – A
+.–=–
Substituindo 1 em 5 temos:
–(+A) = – A
–.+=–
Substituindo 2 em 6 temos:
–(– A)=+A
–.–=+