Universidade Federal do Rio de Janeiro Circuitos Elétricos I – EEL

Universidade Federal do Rio de Janeiro
Circuitos Elétricos I – EEL 420
Módulo 9
Steinmetz
Tesla
Westinghouse
Hertz
Conteúdo
9 - Análise de Regime Permanente Senoidal..............................................................................1
9.1 - Números complexos.......................................................................................................1
9.2 - Fasores e Equações Diferenciais Ordinárias..................................................................1
9.2.1 - Representação de uma senoide por um fasor.........................................................1
9.2.2 - Aplicação do método fasorial às equações diferenciais..........................................3
9.3 - Resposta completa e resposta de regime permanente senoidal......................................6
9.3.1 - Resposta completa..................................................................................................6
9.4 - Impedância e Admitância...............................................................................................9
9.4.1 - Análise de regime permanente senoidal...............................................................10
9.4.2 - Superposição em regime permanente...................................................................10
9.5 - Ressonância..................................................................................................................10
9.6 - Função de Rede Resposta em Frequência e Seletividade.............................................11
9.7 - Potência em regime permanente senoidal....................................................................14
9.7.1 - Potência complexa................................................................................................15
9.7.2 - Valor eficaz...........................................................................................................16
9.8 - Máxima transferência de potência...............................................................................17
9.9 - Normalização da Impedância.......................................................................................18
9.10 - Exercícios...................................................................................................................20
9.11 - Soluções.....................................................................................................................23
Circuitos Elétricos I – EEL420 – UFRJ
2
9 Análise de Regime Permanente Senoidal
9.1 Números complexos
Um número complexo pode ser expresso na forma retangular
A= Aℜ j⋅Aℑ
ou polar
A=∣A∣⋅e j⋅ ou A=∣A∣∢
Onde ∣A∣ é o módulo de A e  é o ângulo de fase ( ∢ ).
Algumas operações importantes com números complexos:
ℜ[ z 1 t z 2 t ]=ℜ[ z 1 t ]ℜ[ z 2 t]
ℜ[a⋅z 1 t]=a⋅ℜ[ z 1 t]
d ℜ [ A⋅e
dt
j⋅⋅t
[
] =ℜ d  A⋅e j⋅⋅t 
dt
]
se ℜ[ A⋅e j⋅⋅t ]=ℜ[ B⋅e j⋅⋅t ] então A= B
se A= B então ℜ[ A⋅e j⋅⋅t ]=ℜ[ B⋅e j⋅⋅t ]
9.2 Fasores e Equações Diferenciais Ordinárias
9.2.1 Representação de uma senoide por um fasor
Uma função do tempo definida como Am⋅cos ⋅t possui amplitude Am ,
frequência angular  e fase  . A soma algébrica desta função com outras de mesma
frequência, ou suas derivadas, resultará em uma nova função de mesma frequência angular.
Circuitos Elétricos I – EEL420 – UFRJ
1
Assim, é de se esperar que, uma vez determinada a frequência da função, ela possa ser tratada
algebricamente pela sua amplitude e fase.
x t = Am⋅cos  j⋅⋅t
x t =ℜ [ Am⋅cos  j⋅⋅t j⋅Am⋅sen  j⋅⋅t ]
x t =ℜ [ Am⋅e j⋅ ⋅t  ]
x t =ℜ [ Am⋅e ⋅e
j⋅
j⋅⋅t
]
j⋅
x t =ℜ [ A⋅e j⋅⋅t ] onde A= Am⋅e
O número complexo A que representa a senoide Am⋅cos ⋅t é chamado de fasor.
Poderíamos ter especificado a senoide em termos da função seno, mas neste caso teríamos que
obter o sinal no tempo a partir da parte imaginária de A⋅e j⋅⋅t . A especificação de um fasor
não carrega informação à cerca da frequência angular do sinal original e por isso, quando se
trabalha com fasores, é necessário conhecer as frequências envolvidas no problema.
Exemplo
v t = 2⋅110⋅cos 2⋅⋅60⋅t/3
A=  2⋅110⋅e
j⋅ /3
v t =ℜ  A⋅e j⋅2⋅⋅60⋅t 
A representação senoidal de frequências é usada principalmente para a determinação
da resposta particular (resposta de regime permanente) da equação diferencial ordinária com
coeficientes reais quando a excitação é uma senoide, ou seja, quando a equação diferencial
que descreve o problema é da forma:
n
n−1
d x
d x
dx
a 0⋅ n a1⋅ n−1 ...a n−1⋅ a n⋅x= Am⋅cos ⋅t
dt
dt
dt
Circuitos Elétricos I – EEL420 – UFRJ
2
9.2.2 Aplicação do método fasorial às equações diferenciais
Seja
d nx
d n−1 x
dx
a 0⋅ n a 1⋅ n−1 ...a n−1⋅ a n⋅x= Am⋅cos ⋅t
dt
dt
dt
onde a 0 , a 1 , ..., a n e Am ,  ,  são constantes reais, os fasores serão
A= Am⋅e
j⋅
e X =X m⋅e
j⋅
Substituindo na equação diferencial
d n ℜ  X⋅e j⋅⋅t 
d ℜ  X⋅e j⋅⋅t 
a 0⋅
...a n−1⋅
a n⋅ℜ  X⋅e j⋅⋅t  =ℜ  A⋅e j⋅⋅t 
n
dt
dt
d n ℜ a 0⋅X⋅e j⋅⋅t 
dt n
d ℜ  a n−1⋅X⋅e j⋅⋅t 
...
ℜ  a n⋅X⋅e j⋅⋅t =ℜ  A⋅e j⋅⋅t 
dt
ℜ [ a 0⋅ j⋅n⋅X⋅e j⋅⋅t ]...ℜ [ a n⋅X⋅e j⋅⋅t ]=ℜ [ A⋅e j⋅⋅t ]
ℜ [ a 0⋅ j⋅n⋅X⋅e j⋅⋅t...a n⋅X⋅e j⋅⋅t ]=ℜ [ A⋅e j⋅⋅t ]
n
a 0⋅ j⋅ ⋅X ...a n⋅X = A
[ a 0⋅ j⋅n...a n ]⋅X =A
X=
A
[ a0⋅ j⋅n...a n ]
∣X∣=
A
 a −a
n
2
2
⋅ 2...   a n−1⋅−a n−3⋅ 3... 
n−2
a n−1⋅ – a n−3⋅ 3... 

∢ X == – arctan
 a n – a n−2⋅2... 
Circuitos Elétricos I – EEL420 – UFRJ
3
Exemplo
Um circuito RLC série é excitado com uma fonte de tensão v S t =∣V∣⋅cos ⋅t .
Calcule a tensão sobre o capacitor em regime permanente.
2
d v C t 
dv t 
L⋅C⋅
 R⋅C⋅ C v C t =v S t 
2
dt
dt
A solução particular é da forma
v C ( t)=|V C|⋅cos (ω⋅t+ ϕ)=ℜ[ V C⋅e j⋅ω⋅t ]
A relação entre o fasor resposta e a excitação é
[ L⋅C⋅ j⋅2 R⋅C⋅ j⋅1 ]⋅V C =V
V C=
V
1− ⋅L⋅C  j⋅⋅R⋅C
|V C|=
2
|V|
√(1−ω ⋅L⋅C ) +( ω⋅R⋅C )
2
∢V C =θ=ϕ– arctan
2
2
(ω⋅R⋅C)
(1−ω 2⋅L⋅C )
v C ( t)=|V C|⋅cos (ω⋅t+θ)
Para o circuito RLC série com R=2, H=1H, C=1F e v S t =10⋅cos t  . Calcular a
resposta forçada do circuito. Realize os cálculos pela forma tradicional e utilizando fasores.
Circuitos Elétricos I – EEL420 – UFRJ
4
di (t)
1
L⋅
+ R⋅i(t )+ ⋅∫ i(t )⋅dt=10⋅cos(t )
dt
C
d 2 i(t) R di (t) 1
10
+ ⋅
+
⋅i (t)=− ⋅sen ( t)
2
L dt
L⋅C
L
dt
sem fasores
i F t= A⋅cos tB⋅sen t
di F t
=−A⋅sen t B⋅cos t 
dt
2
d i F t
dt2
=−A⋅cos t – B⋅sen t
−A⋅cost−B⋅sent2⋅[− A⋅sen tB⋅cost ] A⋅costB⋅sent=−10⋅sen t 
−A2⋅B A=0
−B−2⋅A B=−10
A=5 , B=0
i F t=5⋅cost 
2
d it  R dit 
1
10
 ⋅

⋅i t=− ⋅sen t
2
L
dt
L⋅C
L
dt
com fasores
a saída é da forma
i F (t)=|I F|⋅cos (ω⋅t+θ)=ℜ [ I F⋅e j⋅ω⋅t ]
I F =|I F|⋅e
j⋅θ
Circuitos Elétricos I – EEL420 – UFRJ
5
a entrada v é da forma
v=−

V =|V|⋅e
[

10

⋅cos ⋅t− =ℜ [ V⋅e j⋅⋅t ]
L
2
j⋅π
2
]
R
1
∣V∣
 j⋅   ⋅ j⋅
⋅I F = ⋅e
L
L⋅C
L
2
[ j 2 2⋅ j1]⋅I F =10⋅e
j⋅
2
j⋅
2
10
10
|I F|= 2
= =5
| j + 2⋅j+1| 2
(
)
2
∢I F =θ= π −arctan
=0
2
−1+1
i F (t)=|I F|⋅cos (ω⋅t+θ)=5⋅cos( t+0)
9.3 Resposta completa e resposta de regime permanente senoidal
9.3.1 Resposta completa
y t= y h t p p t para todo t
onde a solução particular escolhida é uma senoide, e por isso pode ser obtida por
fasores. A resposta homogênea pode ser obtida pelos métodos anteriormente descritos, em
função das condições iniciais.
Para o caso particular, com uma única fonte de excitação senoidal e uma só variável de
saída y, podemos escrever
s 1⋅t
s2⋅t
sn⋅t
y t=k 1⋅e k 2⋅e ...k n⋅e  Am⋅cos ⋅t
Circuitos Elétricos I – EEL420 – UFRJ
6
onde k1, k2, …, kn e s1, s2, …e sn dependem das condições iniciais e Am e  dependem
da solução particular
Observa-se que se as raízes da equação característica estiverem no semiplano esquerdo
as exponenciais tendem a zero quando o tempo tende a infinito, restando como resposta y(t),
apenas a solução particular que pode ser obtida usando fasores. Esta é definida como sendo a
resposta de regime permanente senoidal.
Exemplo:
Para o circuito RLC série com R=3/2, L=1/2H, C=1F e v S t =cos 2⋅t ⋅u t 
v S t =10⋅cos t  . Calcular a resposta completa da tensão sobre o capacitor. As condições
iniciais são i L 0– = I 0=2A , v C 0– =V 0=1V .
d 2 v C t 
dv C t 
L⋅C⋅

R⋅C⋅
v C t =v S t 
dt
dt 2
2
1 d v C 3 dv C
⋅ 2  ⋅
v C =u t⋅cos 2⋅t
2 dt
2 dt
−t
v C , h t=k 1⋅e k 2⋅e
−2⋅t
v C , p (t)=ℜ(V⋅e j⋅2⋅t )=|V|⋅cos( 2⋅t +θ)
v S (t )=ℜ( E⋅e
[
j⋅2⋅t
)=cos (2⋅t )
]
1
3
⋅ j⋅ 2 ⋅ j⋅ 1 ⋅V =E
2
2
V=
[
E
1
=
=0,316∢−108,40
−1 j⋅3
1
3
⋅ j⋅2 ⋅ j⋅1
2
2
]
v C , p t=0,316⋅cos 2⋅t – 108,4 0
Circuitos Elétricos I – EEL420 – UFRJ
7
−t
v C t=k 1⋅e k 2⋅e
−2⋅t
0
0,316⋅cos 2⋅t – 108,4 
0
v C 0=1=k 1k 2 0,316⋅cos−108,4 
k 1k 2 =1,1
dv C 0
=2=−k 1 – 2⋅k 2 – 0,316⋅2⋅sen −108,4 0
dt
k 12⋅k 2=−1,4
k 1=3,6 , e k 2=−2,5
−t
−2⋅t
v C t=3,6⋅e −2,5⋅e
0
0,316⋅cos 2⋅t – 108,4 
Como definido anteriormente, se o circuito tem frequências naturais no semiplano
esquerdo ele é estável. Se as frequências naturais estão no semiplano direito então a resposta
de qualquer variável de rede é instável. Se as frequências naturais estão sobre o eixo j⋅
então o circuito apresenta uma resposta natural oscilatória. Se não houver frequências naturais
múltiplas sobre o eixo imaginário nem a excitação apresentar a mesma frequência de uma
destas raízes, então o sistema será estável e a resposta de regime permanente será bem
determinada.
Exemplo: Qual a resposta homogênea de uma rede cujo polinômio característico é
2
2 2
4
2
2
4
S  0  =S 2⋅ 0⋅S 0 .
y h t = k 1⋅k 2⋅t⋅e
j⋅ 0⋅t
− j⋅0⋅t
 k 3k 4⋅t ⋅e
y h t =K 1⋅cos  0⋅t1 K 2⋅t⋅cos 0⋅t2 
Neste exemplo, a resposta natural da rede não é estável pois a rede apresenta
frequências naturais múltiplas sobre o eixo j⋅ . O mesmo acontece se a frequência de
excitação da rede coincide com  0 , mesmo que a rede apresente polinômio característico
2
2
S  0 .
Circuitos Elétricos I – EEL420 – UFRJ
8
9.4 Impedância e Admitância
Em
regime
v (t )=|V|⋅cos( ω⋅t +θ1 ) ,
permanente,
v (t )=ℜ[ V⋅e j⋅(ω⋅t) ]
e
i(t)=|I|⋅cos(ω⋅t +θ2 ) i(t)=ℜ [ I⋅e j⋅(ω⋅t ) ] então podemos reescrever as relações entre corrente
e tensão para o resistor, o capacitor e o indutor
Para o resistor v= R⋅i
Substituindo os fasores na equação acima temos
I =G⋅V ou V =R⋅I
A relação também indica que, como R é um número real, o ângulo de fase entre a
tensão e a corrente é nula, ou seja, θ1=θ 2 .
dv
Para o capacitor i=C⋅
dt
Substituindo os fasores na equação acima temos

I =( j⋅ω⋅C)⋅V ou V =

1
⋅I
j⋅⋅C
Observe que as relações entre os fasores V e I no capacitor são algébricas. Isto leva ao
conceito generalizado de resistência. A generalização da resistência no plano complexo é
chamada de impedância (Z) e a generalização da condutância é chamada de admitância (Y). A
parte imaginária de uma impedância se chama reatância (X) e a parte imaginária de uma
admitância se chama susceptância (B). Sendo assim, em regime permanente senoidal o
capacitor tem um comportamento de reatância capacitiva normalmente representado por XC.
Observe que a reatância do capacitor é um número complexo então os fasores de
tensão e corrente não terão o mesmo ângulo, ou seja, não estarão em fase. Observe também
que a corrente sempre estará adiantada em relação à tensão de um ângulo de 90o.
di
Para o indutor v= L⋅
dt
Circuitos Elétricos I – EEL420 – UFRJ
9
Substituindo os fasores na equação acima temos

I=

1
⋅V ou V = j⋅⋅L⋅I
j⋅⋅L
Observe, novamente, que as relações entre os fasores V e I são algébricas. Assim o
indutor também apresenta uma reatância indutiva normalmente representada por XL. Observe,
ainda, que a reatância indutiva também é um número complexo e a fase entre tensão e
corrente será de 90o. Neste caso porém, diferente do capacitor, a corrente no indutor está
atrasada com relação à tensão.
9.4.1 Análise de regime permanente senoidal
Para regime permanente senoidal, analisado por fasores, valem as mesmas regras de
análise utilizadas circuitos resistivos, pois as leis de Kirchhoff continuam sendo aplicadas.
Assim sendo são válidas as mesmas considerações sobre linearidade e invariância com o
tempo, o que inclui os teoremas de superposição, Thèvenin e Norton bem como associações
de componentes e simplificações e, obviamente, os métodos de análise por correntes de malha
e tensões de nó.
9.4.2 Superposição em regime permanente
Para os casos de circuitos excitados com fontes senoidais, sejam elas de frequências
iguais ou diferentes, podemos utilizar o princípio da superposição para obter a resposta da
variável de rede desejada. A justificativa aqui é igual à estudda anteriormente porém se as
senoides possuírem frequências diferentes não podemos somar diretamente os fasores, pois a
soma de duas ou mais senoides de frequências distintas não é uma senoide.
9.5 Ressonância
Efeito que ocorre quando a impedância é puramente real, ou seja, a reatância
capacitiva se iguala em módulo à reatância indutiva (circuito série), ou a susceptância
capacitiva se iguala em módulo a susceptância indutiva (circuito paralelo). Seja o circuito
RLC paralelo da figura abaixo
Circuitos Elétricos I – EEL420 – UFRJ
10
cuja admitância, no formato Y =G j⋅B , corresponde a
1
1
Y =  j⋅⋅C 
R
j⋅⋅L
onde
G=
1
R
e
B=⋅C –
1
⋅L
Na ressonância B vale zero, ou seja,
⋅C −
1
=0
⋅L
o que ocorre em
0=
1
.
 L⋅C
Observe que num circuito ressonante paralelo a impedância do circuito LC é infinita e
a impedância de um circuito LC ressonante série é zero.
9.6 Função de Rede Resposta em Frequência e Seletividade
Em um circuito RLC paralelo com R=10W, L=5H e C=5F, onde i 0 corresponde a
corrente total fornecida pela fonte e v 0 a tensão sobre os elementos do circuito, então
Circuitos Elétricos I – EEL420 – UFRJ
11

i 0=

1
1
 j⋅⋅C
⋅v
R
j⋅⋅L 0
j⋅⋅i 0=
[
]
j⋅
1
 j⋅2⋅C  ⋅v 0
R
L
[
]
j⋅⋅i 0
j⋅
1
=  j⋅2

⋅v
C
R⋅C L⋅C 0
cujo polinômio característico é da forma
0
⋅S 20
Q
s2 
onde
0=
1

1
e 0=
.
 L⋅C Q R⋅C
Então Q=0⋅R⋅C =

1
C
⋅R⋅C= R⋅
.
L
 L⋅C
Assim
Z=
Z=
v0
i0
=
1
1
1
 j⋅⋅C 
R
j⋅⋅L
R

1 j⋅Q⋅
 0
−
0 

Circuitos Elétricos I – EEL420 – UFRJ
12
Analisando a resposta em frequência deste sistema e buscando pelas frequências de
corte
∣Z∣−3dB=
k
=
2

k


 0
1Q2⋅
−
0 


 2= 1Q 2⋅  − 0
0 

 0
2=1Q ⋅
−
0 
2


±1=Q⋅  − 0
0 
 2±
2

2

2


0
⋅−02=0
Q

1,2 =± 0 ±
2⋅Q
1,2 =±

2

0
 20
2⋅Q

0
1
± 0⋅
1
2
2⋅Q
4⋅Q
Se Q≫1 então
1,2 =±
0
± 0
2⋅Q
Assumindo apenas as soluções positivas
1 =0−
0

e  2=0  0
2⋅Q
2⋅Q
Circuitos Elétricos I – EEL420 – UFRJ
13
Isto determina um pico com largura de banda (BW), tal que
BW =2 −1 =
0
Q


2
2
A frequência do pico é dada por: d =  0− =0⋅ 1−
1
2
4⋅Q
O coeficiente de seletividade também pode ser visto como uma relação entre energia
armazenada no circuito ressonante e a potência dissipada no resistor.
Q=
0
2⋅
=0⋅R⋅C =
0⋅C
G
1 2
1
⋅∣V ∣
⋅C⋅∣V 2∣
0⋅C 2
2
energia armazenada
⋅
= 0⋅
= 0⋅
2
G 1 2
potência média dissipada no R
1 ∣V ∣
⋅∣V ∣
⋅
2
2 R
9.7 Potência em regime permanente senoidal
p t =v t ⋅it 
Circuitos Elétricos I – EEL420 – UFRJ
14
p t =V M⋅cos⋅t ∢V ⋅I M⋅cos ⋅t∢ I 
p t =
V M⋅I M
2
⋅[ cos ∢V −∢ I cos2⋅⋅t∢V ∢ I  ]
Observe que há um nível contínuo somado a uma oscilação de potência com o dobro
da frequência de excitação. O nível médio da potência corresponde a
p t=
V M⋅I M
⋅cos∢V −∢I  .
2
Dependendo do ângulo de fase é possível que a rede alimentada pela fonte de
excitação senoidal absorva e forneça energia. Para capacitores e indutores o ângulo de fase
entre V e I é de 90o e a potência média é zero. Apesar disto a potência instantânea ora é
positiva ora é negativa (toda energia absorvida é devolvida ao circuito). No caso de resistores
o ângulo de fase entre V e I é zero e a potência instantânea nunca fica negativa (o resistor só
absorve energia). Para circuitos RLC o ângulo de fase entre V e I é um valor intermediário e a
rede dissipa parte da energia absorvida e devolve para a fonte parte da energia que ficou
armazenada nos indutores e capacitores.
9.7.1 Potência complexa
S=
V⋅I *
2
onde V e I são fasores
S=
V M⋅e j⋅∢V⋅I M⋅e j⋅−∢ I
∣S∣=
2
V M⋅I M
2
=
V M⋅I M
2
⋅e j⋅∢ V −∢ I
é a potência aparente
S= P j⋅Q
onde
Circuitos Elétricos I – EEL420 – UFRJ
15
S é a potência complexa (VA)
P=
Q=
V M⋅I M
2
⋅cos∢V −∢ I  é a potência média (W).
V M⋅I M
⋅sen ∢V −∢ I  é a potência reativa (VA ou VAR).
2
ϕ=cos (∢V −∢ I ) é o chamado fator de potência (determina quanto da potência
entregue ao circuito está sendo armazenada e quanto está sendo dissipada – transformada em
trabalho)
9.7.2 Valor eficaz
Para um resistor ou rede cujo ângulo de fase entre V e I seja nulo
p t=
V M⋅I M
2
se definirmos V EF =
VM
2
e I EF =
IM
2
então
p t=V EF⋅I EF
Para outras funções não periódicas ou não senoidais o valor eficaz pode ser calculado
como a raiz quadrada da média do sinal ao quadrado (valor RMS).

T
1
X EF = ⋅∫ X t2⋅dt
T 0
O sinal eficaz ou RMS esta relacionado com a energia do sinal e por isso é muito
utilizado em diversas áreas da eletrônica. Os valores de tensão numa instalação elétrica
residencial (220 ou 127 V) são valores eficazes e por isso podem ser utilizados diretamente
para o cálculo de potências.
Circuitos Elétricos I – EEL420 – UFRJ
16
9.8 Máxima transferência de potência
Seja um equivalente Thévenin com fonte de tensão VS e impedância ZS alimentando
uma carga ZL. Qual o valor de ZL para a máxima transferência de energia entre o equivalente
Thévenin e a carga?
1
p= ⋅|I|2⋅ℜ( Z L )
2
I=
VS
Z S Z L
2
1 |V S|
p= ⋅
⋅ℜ(Z L )
2 |Z S + Z L|2
RL
1
p= ⋅|V S|2⋅
2
2
(R L + RS ) +( X L + X S )2
RL
1
p MÁX = ⋅|V S|2⋅
2
( R L + R S )2
então X L =−X S
(R + R )2−2⋅(R L + RS )⋅R L
∂p 1
= ⋅|V S|2⋅ L S
=0
∂ RL 2
(R L + R S )4
ou seja RL =RS
|V S|2
p MÁX =
8⋅RS
cuja eficiência máxima chega a 50%.
Circuitos Elétricos I – EEL420 – UFRJ
17
9.9 Normalização da Impedância
Resistências, indutâncias e capacitâncias de circuitos podem ser consideradas como
impedâncias normalizadas, que estão associadas a frequências normalizadas. Em muitas
aplicações é possível calcular filtros e outros circuitos para um funcionamento normalizado. A
transformação destas impedâncias e das frequências pode ser feito como indicado abaixo.
r n=
valor desejado da impedância
valor da impedância do projeto normalizado
 n=
freqüência desejada
freqüência do projeto normalizado
R=r n⋅R 0
L=
C=
rn
n
⋅L0
C0
r n⋅ n
A vantagem desta estratégia é que um só gabarito de projeto serve para todos os
projetos com qualquer frequência ou impedância. Projetos normalizados sofrem menos
problemas numéricos e erros de arredondamento. Valores normalizados são mais fáceis de
trabalhar do que valores reais.
Exemplo: A figura abaixo mostra um filtro passa baixas com valores de componentes
típicos de circuitos. A função de transferência V 2 / I 1 apresenta ganho unitário em baixas
frequências, e frequência de corte em 1rad/s, conforme gráfico.
Circuitos Elétricos I – EEL420 – UFRJ
18
Supondo que este circuito tenha que ser adaptado para uma situação real onde a
resistência de carga é 600W e a frequência de corte deve ser 3,5kHz. A desnormalização de
frequências e impedâncias é realizada da seguinte maneira.
r n=
valor desejado da impedância
600
=
=600
valor da impedância do projeto normalizado
1
freqüência desejada
2⋅⋅3,5⋅103
 n=
=
=2,199⋅10 4
freqüência do projeto normalizado
1
R=r n⋅R 0=600⋅1=600
L1=
C 1=
C 2=
rn
n
⋅L0=
C0
r n⋅ n
C0
r n⋅ n
600
⋅1,33=36,37⋅10−3
4
2,199⋅10
=
1,5
=0,1338⋅10−6 e
4
600⋅2,199⋅10
=
0,5
=0,0379⋅10−6
4
600⋅2,199⋅10
Circuitos Elétricos I – EEL420 – UFRJ
19
9.10 Exercícios
1) Considere os dois circuitos abaixo: a) calcule as funções de transferência
HR(jw) = VR/V e HC(jw) = VC/V; b) esboce os gráficos de módulo e fase de HR(jw) e HC(jw); c)
determine as frequências de corte para os dois circuitos.
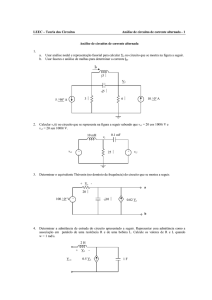
2) Calcule a tensão sobre o indutor em regime permanente senoidal.
Circuitos Elétricos I – EEL420 – UFRJ
20
3) Para cada um dos pares de tensão e corrente corrente abaixo calcule a potência
média nos terminais dos circuitos A e B; em cada caso diga em que direção (de A para B ou de
B para A) flui a potência média calculada.


a) v t =100⋅cos ⋅t−  , it =20⋅cos ⋅t 
4
12
b) v t =100⋅cos ⋅t−
11⋅


 , it =20⋅cos ⋅t
12
4
4) Para o circuito mostrado abaixo: a) Calcule Vo(t) em regime permanente; b) Qual o
período de Vo(t)? c) A resposta está atrasada ou adiantada com relação a Vs(t)? d) Qual é o
valor do avanço/atraso?
Circuitos Elétricos I – EEL420 – UFRJ
21

5) Para os sinais v t =10⋅ 2⋅cos10⋅t  e it =0,45⋅cos 10⋅t – 0,52 : a) Quem
4
está adiantado de quem? b)Quantos graus? c) Quantos segundos?
6) Determinar ZL para a máxima transferência de energia.
7) Para o circuito abaixo, calcular Ix e Vx de regime permanente.
8) Calcule os valores de R8 e L3 para que I(t)=0. Considere o circuito em regime
permanente.
Circuitos Elétricos I – EEL420 – UFRJ
22
9.11 Soluções
1) Considere os dois circuitos abaixo: a) calcule as funções de transferência
HR(jw) = VR/V e HC(jw) = VC/V; b) esboce os gráficos de módulo e fase de HR(jw) e HC(jw); c)
determine as frequências de corte para os dois circuitos.
H R  j  =
V R  j 
V  j 
1
j⋅⋅C⋅R
=
⋅R⋅
=
1
V  j 
V  j  1 j⋅⋅C⋅R
R
j⋅⋅C
j⋅⋅C⋅R 1− j⋅⋅C⋅R 2⋅C 2⋅R2 − j⋅⋅C⋅R
H R  j =
⋅
=
1 j⋅⋅C⋅R 1− j⋅⋅C⋅R
1− 2⋅C 2⋅R2
H R  j =
H C  j =
H C  j =
H C  j =
⋅C⋅R
 1⋅C⋅R
2
∢
[

– arctan ⋅C⋅R
2
]
V C  j 
V  j 
1
1
1
=
⋅
⋅
=
1
V  j 
R j⋅⋅C V  j  1 j⋅⋅R⋅C
j⋅⋅C
1
1− j⋅⋅C⋅R 1− j⋅⋅C⋅R
⋅
=
1 j⋅⋅C⋅R 1− j⋅⋅C⋅R 1− 2⋅C 2⋅R2
1
1⋅C⋅R2
∢[ −arctan⋅C⋅R ]
Circuitos Elétricos I – EEL420 – UFRJ
23
Compare estas respostas com aquelas obtidas do módulo de circuitos de primeira
ordem.
2) Calcule a tensão sobre o indutor em regime permanente senoidal.
Circuitos Elétricos I – EEL420 – UFRJ
24
v L3  j =
V
0,707− j⋅0,707
⋅ j⋅⋅L3 =
⋅ j⋅200⋅0,06=∣V L3∣∢
40 j⋅200⋅0,06
R2 j⋅⋅L 3
v L3 t =∣V L3∣⋅cos 200⋅t
3) Para cada um dos pares de tensão e corrente abaixo calcule a potência média nos
terminais dos circuitos A e B; em cada caso diga em que direção (de A para B ou de B para A)
flui a potência média calculada.


a) v t =100⋅cos ⋅t−  , it =20⋅cos ⋅t 
4
12
b) v t =100⋅cos ⋅t−
11⋅


 , it =20⋅cos ⋅t
12
4
 = 1⋅v MAX⋅i MAX⋅cos ∢v −∢i= 100⋅20⋅cos−45 o−15o =500W
a) P
2
2
potência média fornecida por A
1
100⋅20
o
o
 = ⋅v MAX⋅i MAX⋅cos∢v−∢i =
⋅cos−45 −165 =−866W
b) P
2
2
Circuitos Elétricos I – EEL420 – UFRJ
25
potência média fornecida por B
4) Para o circuito mostrado abaixo: a) Calcule Vo(t) em regime permanente; b) Qual o
período de Vo(t)? c) A resposta está atrasada ou adiantada com relação a Vs(t)? d) Qual é o
valor do avanço/atraso?
a) Vo j =
Vs⋅R1⋅ j⋅⋅R 2⋅C1
Vs
⋅R1=
R ⋅ j⋅X C1
R1⋅ j⋅⋅R2⋅C 1 R2
R 1 2
R2  j⋅X C1
onde =2⋅⋅500
1
1
s
b) Período=T = =
f 500

5) Para os sinais v t =10⋅ 2⋅cos10⋅t  e it =0,45⋅cos 10⋅t – 0,52 : a) Quem
4
está adiantado de quem? b)Quantos graus? c) Quantos segundos?
a) A tensão está adiantada com relação a corrente. Desenhando os fasores que
representam v e i e girando os fasores no sentido anti-horário percebe-se que o fasor de tensão
cruza o eixo real positivo antes do fasor de corrente (normalmente se escolhe o fasor que leva
ao menor ângulo entre os dois fasores).
b) 750 ou 1,31 rad (se optarmos por dizer que a corrente está adiantada com relação a
tensão, o ângulo seria 1050).
c) Uma regra de três resolve o problema. Sabe-se que os cossenos variam a 10rad/s
então 1,31 radiano demora 0,31 s
Circuitos Elétricos I – EEL420 – UFRJ
26
6) Para o circuito abaixo, retire ZL e calcule o equivalente Thévenin do circuito
restante.
Colocando uma fonte de tensão de valor v no lugar de ZL e considerando que uma
corrente i entra nesta fonte temos:
Para o nó A, onde se ligam R, C1 e L
v A−V
v A−v
v A⋅ j⋅⋅C 1
=0
R1
j⋅⋅L
v A=
j⋅⋅L⋅V v⋅R1
j⋅⋅L− 2⋅L⋅C 11
Para o nó B, entre L, C2 e v
v−v A
j ⋅L
[
v⋅
v⋅ j⋅⋅C 2 i=0
]
R1
1
V
–
 j⋅⋅C 2 =
−i
2
3
2
2
j⋅⋅L −⋅L  j⋅⋅L− ⋅L ⋅C 1 
1− ⋅L⋅C 1 j⋅⋅L
Comparando a equação acima com a de um equivalente Thévenin observa-se que:
v⋅Y TH =Y TH⋅V TH −i
7) Para o circuito abaixo, calcular Ix e Vx de regime permanente.
Circuitos Elétricos I – EEL420 – UFRJ
27
O problema só pode ser resolvido por superposição pois as fontes de corrente e tensão
apresentam frequências diferentes.
V2rms ( j ω )=10⋅√13∢−146,3o , V2 =1000
j⋅X L2 = j e j⋅X C1 =− j⋅4
Ix V2  j =
V2
10⋅ 13∢−146,3o 10⋅13∢−146,3o
= 
=
=10∢−90o
o
R1  j⋅X L2 j⋅X C1
2− j⋅3
 13∢−56,3
VxV2  j =R1  j⋅X C1 ⋅Ix V2=2⋅5∢−63,4o ⋅10∢−90o =20⋅ 5∢−153,4 o
Ix V2 t =10⋅ 2⋅sen 1000⋅t
o
VxV2 t =20⋅10⋅sen1000⋅t – 63,4 
o
I2 rms ( j ω )=2⋅√ 2∢135 ,  I2 =2000
j⋅X C2 =− j⋅2
Z EQ= j⋅X L2 //  R1 j⋅X C1 = 2 – j⋅2 //  j⋅2=2 j⋅2
o
o
Vx I2  j =I 1⋅ Z EQ R2 j⋅X C2 =2⋅ 2∢135 ⋅[2 j⋅2 – j⋅22]=8⋅ 2∢135
Ix I2  j =−
I2⋅Z EQ
2⋅ 2∢135o⋅2⋅ 2∢45o 
=− 
=−4∢90o
o
j⋅X L2
2∢−90
Circuitos Elétricos I – EEL420 – UFRJ
28
Ix I2 t =4⋅ 2sen 2000⋅t 
o
Vx I2 t =16⋅cos2000⋅t135 
Ix t =Ix V2 t Ix I2 t
Vx t =VxV2 t Vx I2 t
8) Calcule os valores de R8 e L3 para que I(t)=0. Considere o circuito em regime
permanente.
O circuito pode ser redesenhado como
onde
1
j⋅⋅C 2
− j⋅R7
Z 1= R7 // C2=
=
1
R7⋅⋅C 2− j
R 7
j⋅⋅C 2
R7⋅
Circuitos Elétricos I – EEL420 – UFRJ
29
Z 4=R8 j⋅⋅L 3
A corrente em ZL é zero se
Z1 Z2
=
Z3 Z4
− j⋅R 7
⋅ R  j⋅⋅L 3=R 4⋅R5
R7⋅⋅C 2 8
− j⋅R7⋅ R8  j⋅⋅L3= R4⋅R5⋅ R7⋅⋅C 2 
R7⋅⋅L3 – j⋅R7⋅R8=R 4⋅R5⋅R7⋅⋅C 2 – j⋅R 4⋅R5
Assim
R1⋅⋅L3= R4⋅R5⋅R 7⋅⋅C 2
L3 =R4⋅R5⋅C 2
e
− j⋅R 7⋅R8=− j⋅R4⋅R5
R 8=
R4⋅R5
R7
Circuitos Elétricos I – EEL420 – UFRJ
30