MOVIMENTO VARIADO 01 - (UnB DF) Um objeto, se move numa

MOVIMENTO VARIADO
01 - (UnB DF)
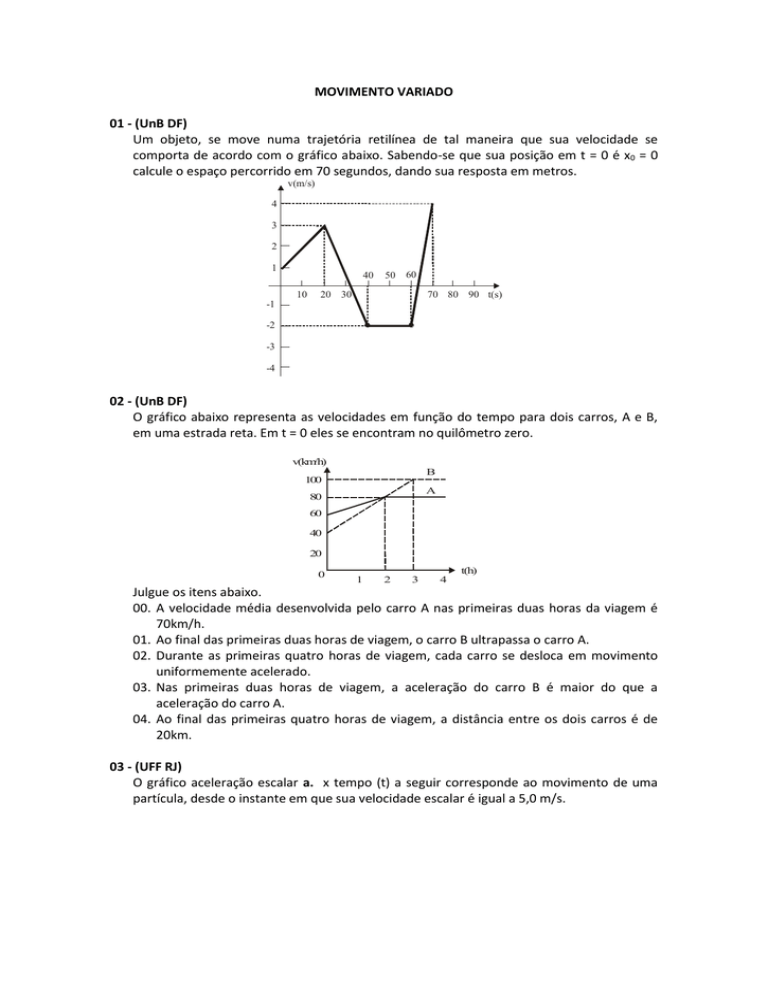
Um objeto, se move numa trajetória retilínea de tal maneira que sua velocidade se
comporta de acordo com o gráfico abaixo. Sabendo-se que sua posição em t = 0 é x0 = 0
calcule o espaço percorrido em 70 segundos, dando sua resposta em metros.
v(m/s)
4
3
2
1
40
10
50
60
20 30
70 80 90 t(s)
-1
-2
-3
-4
02 - (UnB DF)
O gráfico abaixo representa as velocidades em função do tempo para dois carros, A e B,
em uma estrada reta. Em t = 0 eles se encontram no quilômetro zero.
v(km/h)
B
100
A
80
60
40
20
0
t(h)
1
2
3
4
Julgue os itens abaixo.
00. A velocidade média desenvolvida pelo carro A nas primeiras duas horas da viagem é
70km/h.
01. Ao final das primeiras duas horas de viagem, o carro B ultrapassa o carro A.
02. Durante as primeiras quatro horas de viagem, cada carro se desloca em movimento
uniformemente acelerado.
03. Nas primeiras duas horas de viagem, a aceleração do carro B é maior do que a
aceleração do carro A.
04. Ao final das primeiras quatro horas de viagem, a distância entre os dois carros é de
20km.
03 - (UFF RJ)
O gráfico aceleração escalar a. x tempo (t) a seguir corresponde ao movimento de uma
partícula, desde o instante em que sua velocidade escalar é igual a 5,0 m/s.
a (m/s )
2,0
1,0
0
10
20
30
t(s)
-1,0
O valor da velocidade escalar da partícula, no instante 30 s, está expresso na opção:
a) 0 m/s
b) 10 m/s
c) 15 m/s
d) 25 m/s
e) 35 m/s
04 - (UFOP MG)
Observe o gráfico abaixo.
v(m/s)
20
10
0
2
4
6
8
10
t(s)
Calcule:
a) a distância percorrida no intervalo no intervalo de tempo 0  t  10s.
b) as acelerações nos intervalos de tempo 0 < t < 2s, 2s < t < 8s e 8s < t < 10s.
05 - (FUVEST SP)
Um carro viaja com velocidade de 90km/h (ou seja, 25m/s) num trecho retilíneo de uma
rodovia quando, subitamente, o motorista vê um animal parado na sua pista. Entre o
instante em que o motorista avista o animal e aquele em que começa a frear, o carro
percorre 15m. Se o motorista frear o carro à taxa constante de 5,0m/s2, mantendo-o em
sua trajetória retilínea, ele só evitará atingir o animal, que permanece imóvel durante todo
o tempo, se o tiver percebido e uma distância de, no mínimo,
a) 15m
b) 31,25m
c) 52,5m
d) 77,5m
e) 125m
06 - (UFSC)
Um corpo é lançado verticalmente para cima, a partir do chão, com um velocidade inicial
de 30 m/s. Se não houver resistência do ar, e usando g = 10 m/s², determine a soma dos
valores numéricos da altura máxima, em metros, com o tempo de subida, em segundos.
07 - (UNIUBE MG)
Um garoto encontra-se em cima de um viaduto que passa sobre uma rodovia. Ao ver o
movimento, observa um carro que se aproxima, em velocidade constante de 90 km/h e
tenta acerta-lo com uma pedra, verticalmente. Sabendo-se que a altura do viaduto é de 20
m e que g = 10 m/s², a distância que o carro deve ter do viaduto para que o garoto jogue a
pedra e atinja seu objetivo deve ser de:
a) 5 m
b) 25 m
c) 45 m
d) 50 m
e) 100 m
08 - (UNIFOR CE)
Do alto de uma ponte, a 20m de altura sobre um rio, deixa-se cair uma laranja, a partir do
repouso. A laranja cai dentro de uma canoa que desce o rio com velocidade constante de
3,0m/s. No instante em que a laranja inicia a queda, a canoa deve estar a uma distância
máxima da vertical da queda, em metros, igual a:
Dado g = 10m/s2
a) 9,0
b) 6,0
c) 4,5
d) 3,0
e) 1,5
09 - (UFSC)
Um trem, em movimento retilíneo uniformemente desacelerado, reduz a sua velocidade
de 12 m/s para 6 m/s. Sabendo–se que, durante o tempo de 6 segundos, a distância
percorrida foi igual a 54 metros, determine o valor numérico, em m/s², da desaceleração
do trem.
10 - (UNIMEP SP)
Um móvel percorre uma trajetória retilínea de modo que a sua velocidade é representada
pela função V = 40 - 5.t, com todas as unidades no S.I. No intervalo de zero a 8 segundos,
podemos afirmar que:
a) O movimento é uniforme com velocidade constante.
b) O movimento é variado, mas a velocidade é constante.
c) O movimento é uniformemente variado e a aceleração vale, em módulo, 5 m/s2.
d) A aceleração é zero.
e) A aceleração varia de 8 m/s2 para zero.
11 - (UFSC)
Um carro está a 20 m de um sinal de tráfego quando este passa de verde a amarelo.
Supondo que o motorista acione o freio imediatamente, aplicando ao carro uma
desaceleração de 10 m/s², calcule, em km/h, a velocidade máxima que o carro pode ter,
antes de frear, para que ele pare antes de cruzar o sinal.
12 - (INTEGRADO RJ)
Numa rodovia, um motorista dirige com velocidade v = 20 m/s, quando avista um animal
atravessando a pista. Assustado, o motorista freia bruscamente e consegue parar 5,0 s
após e a tempo de evitar o choque.
A aceleração média de frenagem foi, em m/s2, de:
a) 2,0
b) 4,0
c) 8,0
d) 10
e) 20
13 - (UNESP)
Ao passar pelo marco “km 200” de uma rodovia, um motorista vê um anúncio com a
inscrição: “ABASTECIMENTO E RESTAURANTE A 30 MINUTOS”. Considerando que esse
posto de serviços se encontra junto ao marco “km 245” dessa rodovia, pode-se concluir
que o anunciante prevê, para os carros que trafegam nesse trecho, uma velocidade média,
em km/h, de:
a) 80
b) 90
c) 100
d) 110
e) 120
14 - (UFSC)
Uma partícula, efetuando um movimento retilíneo, desloca-se segundo a equação x = – 2
– 4t + 2t2, onde x é medido em metros e t em segundos. O módulo da velocidade
média, em m/s, dessa partícula entre os instantes t = 0s e t = 4s, é:
15 - (UNIUBE MG)
Durante uma viagem pelo interior de São Paulo, um motorista de carro desloca–se
retilineamente com velocidade constante de 72 km/h quando vê uma vaca parada no meio
da estrada a 100m de distância. Imediatamente ele aciona os freios, adquirindo uma
aceleração escalar de módulo 5m/s2. Pode–se afirmar que o motorista
a) não conseguirá evitar a colisão com o animal.
b) conseguirá parar o carro exatamente na frente do animal.
c) conseguirá parar o carro a 60m do animal.
d) conseguirá parar o carro a 50m do animal.
e) conseguirá parar o carro a 40m do animal.
16 - (PUC PR)
Um móvel desloca-se sobre uma trajetória retilínea obedecendo à seguinte equação
horária: d = t² - 5t + 6 (SI)
A equação horária da velocidade do movimento deste móvel é:
a)
b)
c)
d)
e)
v = -5 + 6t
v = -5 - 6t
v = 5 + 6t
v = 6 - 5t
v = -5 + 2t
17 - (UERJ)
A distância entre duas estações de metrô é igual a 2,52 km. Partindo do repouso na
primeira estação, um trem deve chegar à segunda estação em um intervalo de tempo de
três minutos. O trem acelera com uma taxa constante até atingir sua velocidade máxima
no trajeto, igual a 16 m/s. Permanece com essa velocidade por um certo tempo. Em
seguida, desacelera com a mesma taxa anterior até parar na segunda estação.
a) Calcule a velocidade média do trem, em m/s.
b) Esboce o gráfico velocidade X tempo e calcule o tempo gasto para alcançar a
velocidade máxima, em segundos.
18 - (UNIFENAS MG)
A revista ÉPOCA de 2 de agosto de 1999 trouxe uma reportagem sobre a atleta brasileira
Maurren Higa Maggi, medalha de ouro no salto em distância, e prata nos 100m com
barreira nos Jogos Panamericanos de Winnipeg. Segue um pequeno trecho da reportagem:
“Às 18 horas, 25 minutos antes do início da disputa com as outras 11 atletas, Maurren
entrou no Estádio de Atletismo da Universidade de Manitoba para o aquecimento e
sobretudo para os arranjos de pista que combinara com o treinador. Zelosa como uma
costureira, mediu 37,35 metros a partir da marca que antecede a caixa de salto e marcou o
chão com uma fita adesiva. Com o auxílio de um bloco vermelho cedido pelos
organizadores do Pan, marcou à margem da pista também o ponto 31,25 metros. Um
terceiro bloco a auxiliou na marcação de 10,95 metros. Os 37,35 metros é o espaço que
Maurren deve percorrer com 19 passadas e num tempo máximo de 4,50 segundos.”
Supondo que Maurren percorra os 37,35m em movimento uniformemente variado e parta
da marca feita com fita adesiva, a mínima aceleração que a atleta deve imprimir é de,
aproximadamente,
a) 3,69 m/s2.
b) 3,09 m/s2.
c) 2,47 m/s2.
d) 1,47 m/s2.
e) 1,08 m/s2.
19 - (ACAFE SC)
Dirija devagar na chuva!
Um automóvel, movendo-se com velocidade de módulo 10m/s (36km/h) numa estrada
asfaltada, num dia ensolarado, é freado e desloca-se 7,0m até parar. Nas mesmas
circunstâncias, só que sob chuva, necessita de 8,0m para parar. Supondo-se que sua
velocidade seja de módulo 30m/s (108km/h), precisará, num dia de chuva, _____ metros a
mais para parar nesta estrada, do que num dia ensolarado.
A alternativa VERDADEIRA, que completa o enunciado acima, é:
a) sete
b) cinco
c) nove
d) três
e) onze
20 - (UNIFENAS MG)
Um móvel parte do repouso com aceleração constante e, em 2 segundos de movimento,
se desloca 24 metros. A velocidade desse móvel no instante 2 segundos do movimento é:
a) 6 m/s.
b) 12 m/s.
c) 24 m/s.
d) -24 m/s,
e) -12 m/s,
GABARITO:
1) Gab: 20
2) Gab: 00. C 01. E 02. E 03. C 04. E
3) Gab: B
4) Gab:
a) 170m;
b) entre 0 e 2s a1 = 5m/s2, entre 2s e 8s é nula, entre 8s e 10s a2 = -10m/s2.
5) Gab: D
6) Gab: 48
7) Gab: D
8) Gab: B
9) Gab: 01
10) Gab: C
11) Gab: 72
12) Gab: B
13) Gab: B
14) Gab: 04
15) Gab: C
16) Gab: E
17) Gab:
a) 14m/s
b) 22,5s
18) Gab: A
19) Gab: C
20) Gab: C