Números Complexos e Geometria Analítica

Colégio Modelo
Exercícios de Números Complexos e Geometria Analítica
Professor Diniz – site: www.diniz.webnode.com.br
Bom Estudo!
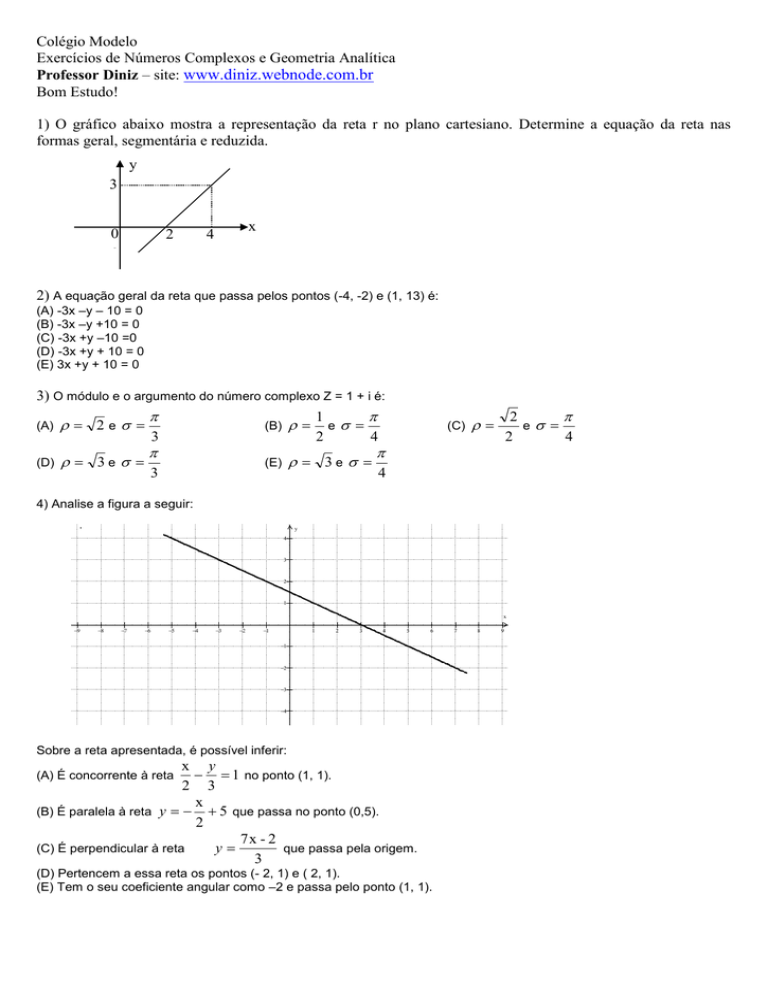
1) O gráfico abaixo mostra a representação da reta r no plano cartesiano. Determine a equação da reta nas
formas geral, segmentária e reduzida.
y
3
0
o
2
x
4
2) A equação geral da reta que passa pelos pontos (-4, -2) e (1, 13) é:
(A) -3x –y – 10 = 0
(B) -3x –y +10 = 0
(C) -3x +y –10 =0
(D) -3x +y + 10 = 0
(E) 3x +y + 10 = 0
3) O módulo e o argumento do número complexo Z = 1 + i é:

1

(A)   2 e  
(B)   e  
3
2
4


(D)   3 e  
(E)   3 e  
3
4
(C)
2

e 
4
2

4) Analise a figura a seguir:
y




x



















Sobre a reta apresentada, é possível inferir:
x y
  1 no ponto (1, 1).
2 3
x
(B) É paralela à reta y    5 que passa no ponto (0,5).
2
7x - 2
y
(C) É perpendicular à reta
que passa pela origem.
3
(A) É concorrente à reta
(D) Pertencem a essa reta os pontos (- 2, 1) e ( 2, 1).
(E) Tem o seu coeficiente angular como –2 e passa pelo ponto (1, 1).



5) A figura a seguir representa um triângulo cujos vértices são números complexos:

5
5 
 2cos2   isen2, Z 2  2 cos   isen   
 6 
  6 
  4 
 4  
e Z 3  2 cos
  i sen 
  , escreva Z1, Z2 e Z3 na forma algébrica.
 3 
  3 
Sabendo que: Z1
Na figura abaixo, o ponto P é o afixo do número complexo z = a + bi no plano de Argand-Gauss. Escreva
esse número complexo na forma polar:
6)
7) ESCREVA na forma trigonométrica os números complexos z =
3  i e w = 2 2 (1  i ) .
8) (UFF-2002) Considere a representação a seguir em que a reta r é perpendicular às retas s e t. Determine a
equação da reta t, sabendo que UV=2.PQ.
9) O gráfico apresenta duas retas perpendiculares entre si. Sabendo que OA  2 e OB  4 , determine:
a) a equação da reta r e s.
y
b) a área do triângulo ABC.
s
r
C
x
0
2
–4
10) No gráfico a seguir, determine a equação da reta r que passa pelo ponto P e é perpendicular à reta s.
y
5
0
-1
x

P
-2
s
11) Multiplicando-se o número complexo z = 2 + 2i pela unidade imaginária i, obtém-se um número complexo cuja
representação, no plano, correspondente a um ponto PERTENCENTE À RETA de equação.
a) y = -x
b) y = - 2x + 2
c) y = x
d) y = -2x
e) y = 2x
12) Seja o número complexo z = 1 + i. O ARGUMENTO PRINCIPAL de z² é:
a) 30º
b) 45º
c) 0º
d) 90º
e)120º
13) Considere o número complexo 1 + i 3 e faça o que se pede.
A) Determine seu MÓDULO E ARGUMENTO PRINCIPAL.
B) Coloque-o na FORMA TRIGONOMÉTRICA.
C) Faça a representação GRÁFICA.
14) ESCREVA o número
5  5i
na forma polar.
2  2i
15) O gráfico seguinte representa uma função f, tal que f : IR  IR . A LEI que REPRESENTA a função f é:
A)
B)
C)
D)
E)
f (x) = 2x + 3
f (x) = - 2x – 3
f (x) = -2x + 3
f (x) = x + 3
f (x) = -1,5x + 3
16) Sabendo-se que a inclinação da reta r que passa pelos pontos (a, 0) e (1, -2) é
1
. ENCONTRE:
2
a) o VALOR DE a.
b) a EQUAÇÃO REDUZIDA da reta r.
17) QUAL das afirmativas a seguir é INCORRETA?
A)
B)
C)
D)
E)
Se r: y = 3 e s: x = 4, então r e s são perpendiculares.
Se r: 2x + y – 3 = 0 e s: x – 2y + 4 = 0, então r e s são perpendiculares.
Se r: 2x + y – 3 = 0 e s: y = 2x + 7, então r e s são paralelas.
Se r: -4x + 2y + 6 = 0 e s: x + 2y - 4 = 0, então r e s são concorrentes e cruzam no ponto (2,1),
Se r: x + 2y – 4 = 0 e s: 6x + 12y - 1 = 0, então r e s são paralelas.
18) As retas m e r da figura seguinte são perpendiculares. Com base nessas informações é CORRETO afirmar que
a) A equação da reta m é y = x + 1.
b) A equação da reta r é y = -x – 3.
c) A área do triângulo ABC é 16 u.a.
d) O segmento AC mede 6.
e) O menor ângulo formado pela
reta s e segmento AB vale 30°.
Professor Diniz – site: www.diniz.webnode.com.br
RESPOSTAS
1) 3x – 2y – 6 = 0 ; x/2 + y/-3 = 1 ; y = 3x/2 – 3
2) C
3) C
4) B
5) Z1 = 2; Z2 =  3  i e Z3 =  1 3i
5
5
 i sen )
6) z = 2.(cos 300° + isen300°) ou z  2(cos
3
3




7) z  2(cos  i sen ) e w  4(cos  i sen )
6
6
4
4
8) Resp.: y = – x + 4
x
 1 b) A = 5 u.a.
9) a) Reta r: y = 2x – 4 ; Reta s: y =
2
10) x – 2y – 9 = 0
11) A
12) D

13) A) z = 2 e  
3



B) z = 2  cos  isen 
3
3

C)
3
14)
5


 cos  isen 
2
2
2
15) C
16) a) a = 5 b) y =
1
5
x
2
2
17) C
18) C
Professor Diniz – site: www.diniz.webnode.com.br
Contatos:
E-mail: [email protected]
Site: www.diniz.webnode.com.br
Orkut: Professor Diniz.
Facebook: www.facebook.com/professordiniz
Blog: www.amigosdoprofessordiniz.blogspot.com