caracterização de materiais magnéticos a baixo - TEDE

UNIVERSIDADE DO ESTADO DE SANTA CATARINA
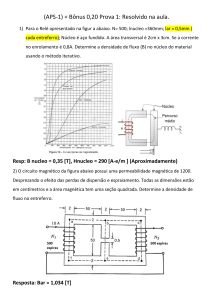
CENTRO DE CIÊNCIAS TECNOLÓGICAS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA
ELÉTRICA
LEONARDO JOSÉ AMADOR SALAS MALDONADO
CARACTERIZAÇÃO DE MATERIAIS MAGNÉTICOS A
BAIXO CUSTO APLICADA À OBTENÇÃO DOS
PARÂMETROS DE UM DISPOSITIVO
ELETROMAGNÉTICO
JOINVILLE
2015
UNIVERSIDADE DO ESTADO DE SANTA CATARINA
CENTRO DE CIÊNCIAS TECNOLÓGICAS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA
ELÉTRICA
LEONARDO JOSÉ AMADOR SALAS MALDONADO
CARACTERIZAÇÃO DE MATERIAIS MAGNÉTICOS A
BAIXO CUSTO APLICADA À OBTENÇÃO DOS
PARÂMETROS DE UM DISPOSITIVO
ELETROMAGNÉTICO
Dissertação submetida ao Programa
de Pós-Graduação em Engenharia Elétrica do Centro de Ciências Tecnológicas da Universidade do Estado de
Santa Catarina, para a obtenção do
Grau de Mestre em Engenharia Elétrica.
Orientador:
Prof. Dr. Antônio F. L.
Nogueira
Coorientador:
de A. B. Filho
JOINVILLE
2015
Prof. Dr. Adalberto
CARACTERIZAÇÃO DE MATERIAIS MAGNÉTICOS A
BAIXO CUSTO APLICADA À OBTENÇÃO DOS
PARÂMETROS DE UM DISPOSITIVO
ELETROMAGNÉTICO"
"
por
Leonardo José Amador Salas Maldonado
Esta Dissertação foi julgada adequada para a obtenção do título de
Mestre em Engenharia Elétrica
e aprovado em sua forma nal pelo
PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA
ELÉTRICA DO
CENTRO DE CIÊNCIAS TECNOLÓGICAS DA
UNIVERSIDADE DO ESTADO DE SANTA CATARTINA
Prof. Dr. Antônio F. L. Nogueira
CCT/UDESC (Orientador/presidente)
Banca Examinadora:
Joinville, 27 de fevereiro
de 2015.
Prof. Dr. Ademir Nied
CCT/UDESC
Prof. Dr. Mauricio V. F. da Luz.
UFSC
Prof. Dr. José de Oliveira
CCT/UDESC (Suplente)
À minha esposa, Sttela Maris, pelo apoio
e compreensão.
Aos meus lhos, Alessandra, Fernando e
Leonardo Vinicius, por alegrarem a minha vida.
Às minhas famílias, chilena e brasileira.
Aos meus saudosos pais, Liliana e Evaristo.
AGRADECIMENTOS
A realização deste trabalho foi possível graças à cooperação de
várias pessoas que se dedicaram ao longo do progresso desta contribuição cientíca. Gostaria de agradecer a todos que contribuíram para o
desenvolvimento desta dissertação, em especial:
à minha esposa, Sttela Maris, por sua ajuda na escrita e revisão
ortográca e por seu apoio e carinho;
ao meu orientador, o doutor Antônio Flavio Licarião Nogueira,
por sua orientação e material didático, primordiais para evolução deste
trabalho. Obrigado por sua dedicação e motivação;
ao meu coorientador, o mestre Adalberto de Araújo Barreto
Filho, por suas valiosas sugestões e material bibliográco;
ao meu ex-aluno, Gabriel Hermann Negri, pelo auxílio com os
códigos em Lua;
ao meu ex-aluno, Arthur Garcia Bartsch, pela digitação e sugestões.
A Lebre e a Tartaruga
mostra a im-
portância da perseverança, uma história
contada por Esopo, fabulista grego do século VII AC, ou como eram chamados:
"Peda-gogos", escravo de jogos.
O en-
sino fundamental, para os gregos, começava por princípios morais e éticos.
"Só sei que nada sei".
Sócrates. No
início, acredita-se em ideias e conceitos,
com o tempo se percebe o quão errado
pode-se estar.
Esta dissertação vai ao encontro de muitas dúvidas e o reaver de conceitos ditos
básicos", mas que termina apresentando
o quanto a natureza pode ser complexa.
Frente a isso, só resta a perseverança da
busca de uma resposta, que alguns chamam de modelo outros de teoria.
RESUMO
Este trabalho apresenta uma síntese do estado da arte sobre as caracterizações e perdas no ferro sob o enfoque da Engenharia Elétrica;
pretende-se compreender e gerar subsídios para a caracterização de materiais ferromagnéticos a baixo custo, aplicado na avaliação de parâmetros eletromagnéticos e de eciência energética de dispositivos eletromagnéticos, através de uma visão qualitativa dos fenômenos eletromagnéticos complexos auxiliando na compreensão e estudo do projeto de
máquinas elétricas.
Palavras-chave:
Contactores; Indutância; Método dos Elementos Fi-
nitos; Perdas magnéticas; Programas de Simulação; Transformadores
ABSTRACT
This work presents a state of the art synthesis about the characterization and losses in iron under the focus of Electrical Engineering; it is
intended to understand and to generate aids to ferromagnetic materials
characterization at low cost, applied in the evaluation of electromagnetic parameters and energetical eciency of electromagnetic devices,
using a qualitative view of complex electromagnetic phenomena, helping in the comprehension and in the study of the electrical machines
project.
Keywords:
Contactors; Inductance; Finite Element Method; Magne-
tic Losses; Simulation Software; Transformers
LISTA DE FIGURAS
Figura 1.1
Laços de histerese, operação quase-estática. . . . . . . . . . . .
Figura 1.2
Intensidade de campo
H
d. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Figura 1.3 Laços de histerese, f = 50 Hz. . . . . . . . . . . . . . . . . . . . . . . . .
Figura 1.4 Laços de histerese, f = 250 Hz. . . . . . . . . . . . . . . . . . . . . . . .
sura
Figura 1.5
Figura 2.1
40
em uma laminação de espes41
42
43
Característica de magnetização, linearizada por partes. 45
Malhas formadas por elementos triangulares de pri-
meira ordem; (a) malha incorreta; (b) malha correta. . . . . . . . . . . . .
51
Figura 2.2
Funções planares
αi (x, y). . . . . . . . . . . . . . . . . . . . . . . . . . . . .
53
Figura 2.3
Funções planares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
54
Figura 2.4
Os elementos 1, 2, 3 e 4 compartilham o nó a. . . . . . . .
55
Figura 3.1
Grão orientado (GO). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
Figura 3.2
Grão não-orientado (GNO). . . . . . . . . . . . . . . . . . . . . . . . . . .
66
Figura 3.3
O dipolo magnético tem origem no momento angular
dos elétrons nos íons ou átomos que formam a matéria. . . . . . . . . . .
Figura 3.4
67
Através do diagrama de Linus Pauling, obtém-se a dis-
tribuição dos elétrons nos orbitais. No caso do ferro são 4 momentos angulares de spin não nulos, isto é, 4 magnétons de Bohr. . . .
Figura 3.5
68
O tamanho dos domínios está na escala micrométrica
e, para um material policristalino, cada grão pode conter mais de
um domínio. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Figura 3.6
70
Ilustração da parede do domínio magnético que separa
dois domínios cujos momentos atômicos mudam a orientação em
◦
180 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
Figura 3.7
Metalograa do núcleo do transformador fabricado na
China aço 1010. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Figura 3.8
A existência de domínios magnéticos é resultado da mi-
nimização de energia. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Figura 3.9
72
Mecanismo de magnetização não-linear do núcleo. . . . .
73
74
Figura 3.10 Curva aproximada da magnetização em um material
ferromagnético (não linear) obtida pelo produto ponto a ponto
M = Hµr
do gráco permeabilidade versus intensidade de campo. 75
Figura 3.11 Curva de magnetização inicial de um material ferromagnético, na região de deslocamento de domínio. . . . . . . . . . . . . . . .
76
Figura 3.12 Processo de magnetização do material sob o enfoque do
balanço energético. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
76
Figura 3.13 Lâmina de um material ferromagnético. . . . . . . . . . . . . . .
80
Figura 3.14 Formas de onda estilizadas de tensão PWM e da corrente que é proporcional à indução.
A série de Fourier permite
representar qualquer função como uma soma de ondas senoidais
com diferentes amplitudes e frequências. . . . . . . . . . . . . . . . . . . . . . . . . . 83
Figura 3.15 A técnica PWM gera uma onda de corrente distorcida
que acompanha a senoide de referência, por efeito da integração
da corrente, com base na constante de tempo
RL do circuito.
Esse
processo de integração gera exponenciais crescentes e decrescentes
que dão o caráter "recortado"ao sinal de corrente. . . . . . . . . . . . . . . .
Figura 3.16 Forma da curva
BH
84
para uma forma de tensão PWM
as ondas recortadas, afetam só o contorno da curva de histerese,
seu efeito sobre as perdas totais é mínimo, num inversor PWM as
perdas cam por conta do aumento da frequência. . . . . . . . . . . . . . . .
85
Figura 3.17 Os dois tipos básicos de forma de distorção da indução magnética na formação de laços menores na curva de histerese
magnética: (a) sem extremos locais e (b) quatro variações extremas no período. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
85
Figura 3.18 As susceptibilidades diferenciais são as inclinações das
retas apresentadas na Fig.
O algoritmo de Peuget (PEUGET,
1995) é aplicado para o encontro de um primeiro possível conjunto
de parâmetros. Utiliza-se metade de um laço de histerese para a
obtenção dos nove dados de entrada para o algoritmo. . . . . . . . . . . .
87
Figura 3.19 Pontos chaves sugeridos por Jiles para obtenção dos
nove dados (Ms ,
Mm , Hm , χm , Mr , χr , Hc , χc ,
Hc,
χin )
necessá-
rios para a implementação do modelo JA estão indicados na gura
traçada a 1 Hz. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
88
Figura 3.20 Transformador modelado no FEMM. . . . . . . . . . . . . . . . . .
89
Figura 3.21 Aparelho de medida DW20. . . . . . . . . . . . . . . . . . . . . . . . . . .
90
Figura 3.22 Quadro de Epstein - foto. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
Figura 3.23 Quadro de Epstein - ilustração. . . . . . . . . . . . . . . . . . . . . . . .
92
Figura 3.24 Circuito esquemático para realização do teste de perdas
BH . . . . . . . . . . . . . . . . . . . . . . . .
92
Figura 3.25 Esquema do sensor SST. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
93
Figura 3.26 Sensor de lâmina única SST. . . . . . . . . . . . . . . . . . . . . . . . . .
94
magnéticas e levantamento da curva
Figura 3.27 Exemplo de OIM e código de cores. . . . . . . . . . . . . . . . . . . . 94
Figura 3.28 Laminação . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
Figura 3.29 Magnetização em relação aos índices de Miller de uma
estrutura CCC (Cúbica de Corpo Centrado). . . . . . . . . . . . . . . . . . . . .
96
Figura 3.30 Circuito para obtenção da curva de histerese. . . . . . . . . .
97
Figura 3.31 Formas de onda dos campos
H(t) e B(t),
proporcionais
aos sinais de corrente primária e tensão secundária. . . . . . . . . . . . . . . 99
Figura 3.32 Curva de histerese do transformador construído utilizando osciloscópio digital com amostragem de 500 pontos. . . . . . . .
Figura 3.33 Denição do comprimento médio adotado lm
99
= 0, 1686 m.100
Figura 3.34 O efeito de histerese é gerado pela resistência à movimentação de paredes de domínio. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
Figura 3.35 Formato do laço de histerese de acordo com o tipo de
material. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
Figura 3.36 Obtenção ponto a ponto da curva de magnetização
BH
a partir da curva de histerese. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
Figura 3.37 Curva de magnetização levantada experimentalmente. 104
Figura 3.38 Curva
BH
de aço carbono 1010. Nessa nomenclatura,
o número 1000 corresponde família de aços de baixo carbono, enquanto o número 10 corresponde ao teor de 0,1% de carbono. . . . . 105
Figura 3.39 Curva de magnetização em relação à intensidade de
campo, obtida a partir da curva de histerese levantada pelo circuito
proposto. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
Figura 3.40 Permeabilidade magnética relativa em função da intensidade de campo. Teoricamente, esta curva deveria partir do zero.108
Figura 3.41 Permeabilidade magnética relativa em função da corrente de excitação primária. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
Figura 3.42 A curva da indutância primária é obtida multiplicando
as ordenadas da característica permeabilidade versus corrente pelo
fator
KL1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
Figura 3.43 Utilizando programa de elementos nitos, a indutância
foi calculada considerando uma corrente de magnetização de 50
[mA]. Mas, existe um erro nesse valor porque a corrente de vazio
é a soma da corrente de magnetização de 47 [mA] e uma outra
corrente, associada as perdas do ferro, considerando resistor equivalente
Rn = 12665 [Ω],
cujo valor é 17 [mA]. Assim, refazendo as
contas com 47 [mA], se obtém a curva corrigida, sendo essa muito
próxima da curva experimental. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
Figura 3.44 Indutância própria secundária, obtida através do fator
de proporcionalidade
KL2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
112
Figura 3.45 Indutância mútua vista do secundário por efeito da corrente primária. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
Figura 3.46 Curva da relutância em função da corrente primária. . 116
Figura 3.47 Curva da permeância do circuito primário em função
da corrente de magnetização no enrolamento primário. . . . . . . . . . . 117
Figura 3.48 Distribuição de correntes em um transformador real. . . 118
Figura 3.49 Indutância primária de 8,28 [H] no ponto de operação. 121
Figura 3.50 Indutância secundaria de 0,095 [H] no ponto de operação. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
Figura 3.51 Curva indutância mútua em função da corrente primaria na condição sem carga o valor para a indutância gracamente
está em torno de 0,903 [H] para uma corrente de primaria de 100
[mA] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
Figura 3.52 Modelo ideal de transformador monofásico. . . . . . . . . . . . 123
Figura 3.53 Circuito para cálculo das mútuas. . . . . . . . . . . . . . . . . . . . . 124
Figura 3.54 Circuito para cálculo das mútuas. . . . . . . . . . . . . . . . . . . . . 124
Figura 3.55 Modelo série do transformador utilizado pelo FEMM. . 127
Figura 3.56 Transformação circuito série para circuito paralelo. . . . 127
Figura 3.57 Forma de onda da corrente de excitação em vazio para
uma corrente de 100mA, torna-se necessário aumentar a tensão
para atingir este valor. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
Figura 3.58 Forma de onda da corrente e tensão no ensaio de curto
circuito. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
Figura 3.59 Modelo circuital do transformador. . . . . . . . . . . . . . . . . . . . 132
Figura 3.60 Modelo circuital do transformador reetido ao primário.132
Figura 3.61 Forma de onda da corrente e tensão no ensaio de curto
circuito. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134
Figura 3.62 Modelo série do ensaio de curto circuito no transformador. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135
Figura 3.63 Curva de histerese correspondente aos ciclos de perdas
do ferro:
(a) perdas por histerese; (b) perdas por correntes de
Focault; (c) perdas excedentes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
Figura 3.64 Derivando a curva
BH
se obtém a curva de perme-
abilidade incremental, em que percebe-se que o ponto de menor
relutância coincide com uma intensidade de campo
H = 100 [A/m].141
Figura 3.65 Curva de histerese traçada a 10 Hz . . . . . . . . . . . . . . . . . . . 145
Figura 3.66 Separação perdas em função da Indução. . . . . . . . . . . . . . 146
Figura 3.67 Operação em regime quase estático: as perdas de histerese são muito próximas das perdas totais. . . . . . . . . . . . . . . . . . . . . . 146
Figura 3.68 Separação das perdas em função da frequência. . . . . . . . 147
Figura 3.69 Circuito não-linear para representação de um transformador com secundário em vazio. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
Figura 3.70 Fluxo de enlace em função do tempo logo após a energização do transformador. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149
Figura 3.71 Fluxo de enlace e corrente de
in-rush
em um transfor-
mador. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151
inrush. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
Figura 3.72 Circuito considerado para o cálculo da corrente de
Figura 3.73 Curva
BH
gem de 500 pontos.
do material obtida através de uma amostra-
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
Figura 3.74 Corrente transitória
in-rush
de valor máximo 1,3 [A].
O transitório se mantém por 20 ciclos de rede aproximadamente. 157
Figura 3.75 Tendências da corrente de
in-rush. . . . . . . . . . . . . . . . . . . . . 157
Figura 3.76 A corrente de pico na condição permanente atinge um
valor máximo de 55 mA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 158
Figura 3.77 Linhas de uxo no transformador simulado. . . . . . . . . . . . 158
Figura 3.78 Modelo do núcleo na obtenção da curva de magnetização. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161
Figura 3.79 Correção na curva BH experimental em função da corrente associada as perdas do ferro. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162
Figura 3.80 A diferença nas curvas de indutâncias primaria
L1
teó-
rica e experimental é produzida pela corrente de vazio. Essa corrente afeta a curva
BH
e, consequentemente, a permeabilidade
absoluta do material. Outro efeito dessa corrente é a redução da
relação de transformação. Isso diculta signicativamente o processo de determinação das indutâncias de dispersão primária e
secundária. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162
Figura 3.81 Modelo de núcleo com correntes de compensação. . . . . . 163
Figura 3.82 Variação na relação de transformação por efeitos da
corrente de vazio
I0 ,
o transformador atinge seu valor de projeto,
neste caso de 9.17, com uma corrente iguais ou superior a nominal.
Os valores experimentais estão indicados com 'x'. . . . . . . . . . . . . . . . 164
Figura 4.1
Dimensões do contactor em estudo. . . . . . . . . . . . . . . . . . . . 167
Figura 4.2
Sombreamento dos polos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 168
Figura 4.3
Contorno utilizado para realização dos cálculos. . . . . . . . 169
Figura 4.4
Vista frontal do contactor em estudo. . . . . . . . . . . . . . . . . . 170
Figura 4.5
Parte xa do contactor. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170
Figura 4.6
Contactor implementado no FEMM. . . . . . . . . . . . . . . . . . . 171
Figura 4.7
Bobina de espiras conhecidas para determinar a tensão
induzida por espira. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172
Figura 4.8
Montagem da bobina de espiras conhecidas que permite
avaliar a tensão por espira. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173
Figura 4.9
Diagramas dos uxos gerados pela bobina principal e a
espira de sombra. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174
Figura 4.10 Material Carpenter Silicon Iron da biblioteca do Femm.175
Figura 4.11 Material Carpenter Silicon Iron com entreferro de 0,4mm.175
Figura 4.12 Circuito proposto para dispositivos com uma única bobina de excitação. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 176
Figura 4.13 Forma de onda da tensão CH2 (B) e corrente com baixo
conteúdo harmônico CH1(H). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178
Figura 4.14 Curva de histerese do material para a corrente nominal (75mA), sua acentuada inclinação se deve a presença de um
minúsculo entreferro de 0,4mm, na trave central. . . . . . . . . . . . . . . . . 179
Figura 4.15 Curva experimental de Histerese do material utilizado
no núcleo, sua acentuada inclinação se deve a presença de um
minúsculo entreferro de 0,4mm, na trave central, da mesma forma
que na operação nominal. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 180
Figura 4.16 Em azul, a curva
BH
do modelo de simulação do mate-
rial Carpenter com o efeito do entreferro e, em vermelho, a curva
do material obtido experimentalmente. . . . . . . . . . . . . . . . . . . . . . . . . . 181
Figura 4.17 Gráco da permeabilidade relativa em função da intensidade de campo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 182
Figura 4.18 Representação do contactor fechado e do circuito elétrico simplicado equivalente.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 183
Figura 4.19 Gráco de relutância do material e em função de entreferros. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184
Figura 4.20 Curva aproximada da permeância experimental do contactor. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 187
Figura 4.21 Linhas de uxo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 188
Figura 4.22 Gráco da curva
λi,
regiões de energia e coenergia. . . . 190
Figura 4.23 Entreferro e espalhamento associado. . . . . . . . . . . . . . . . . . 195
Figura 4.25 Gráco da curva de saturação magnética BH do mesmo
material anterior com um entreferro de 5mm, é possível perceber
que em função deste grande entreferro a curva se torna linear. . . . 197
Figura 4.26 Espalhamento do uxo magnético no entreferro e energia acumulada. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 199
Figura 4.27 Contorno para o cálculo do campo. . . . . . . . . . . . . . . . . . . . 201
Figura 4.28 Força produzida no contactor por uma corrente alternada (azul) e por uma contínua (vermelha) com um entreferro
variando de zero até 5mm. Em verde, o tensor ponderado. . . . . . . 203
Figura 4.29 Modelo elétrico do contactor no FEMM, a indutância e
o resistor equivalente estão em série. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 204
Figura 4.30 Modelo elétrico do contactor, a indutância e o resistor
equivalente estão em paralelo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205
Figura 4.31 Perdas no núcleo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206
Figura 4.32 Formato de onda da corrente sem entreferro. . . . . . . . . . . 207
Figura 4.33 Formato de onda da corrente com entreferro. . . . . . . . . . 208
Figura 4.34 Espectro da forma de onda da corrente sem entreferro
(THD = 32,14%). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 208
Figura 4.35 Espectro da forma de onda da corrente com entreferro
(THD = 5,2%). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209
Figura 4.36 Montagem de transformador inserindo um entreferro de
0,4mm. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 210
LISTA DE TABELAS
Tabela 3.1
Materiais ferrocristalinos: propriedades eletromagnéti-
cas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Tabela 3.2
usados em núcleos de transformadores. . . . . . . . . . . . . . . . . . . . . . . . . .
Tabela 3.3
63
Algumas características de materiais ferromagnéticos
67
Classicação dos materiais quanto à susceptibilidade
magnética e a relação de permeabilidade. . . . . . . . . . . . . . . . . . . . . . . . .
73
Tabela 3.4
Resumo dos dados construtivos do transformador. . . . . 100
Tabela 3.5
Exemplos de materiais duros, moles e intermediários . . 102
Tabela 3.6
Perdas por massa usuais em máquinas de corrente al-
ternada . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
Tabela 3.7
Perdas para diferentes frequências de operação, em [Hz].
A perda total simulada
Ps
e a perda total do modelo
Pe
são apre-
sentadas em [W]. As parcelas de perdas dos modelos são expressas
em [W] e em %. Nesse último caso, representa o quanto essa parcela contribui percentualmente para as perdas do dispositivo em
uma frequência especíca. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144
Tabela 3.8
Percetual de hamônicos de corrente utilizados por relés
diferenciais para evitar disparos desnecessários. . . . . . . . . . . . . . . . . . . 152
Tabela 3.9
Resultados da simulação no FEMM. . . . . . . . . . . . . . . . . . . 159
Tabela 3.10 Síntese dos cálculos de indutância no ponto de operação
I0 = 23, 19+j46, 9,
I2 = aI10 = 0, 5972 . . . . . . . . . . . . . 161
do transformador. Para os cálculos, considerar
I10 = 65, 13, I1 = 88, 32 + j46, 9
Tabela 4.1
e
Dados geométricos do núcleo magnético, contactor fe-
chado. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 167
Tabela 4.2
Parâmetros do circuito de excitação. . . . . . . . . . . . . . . . . . . 177
Tabela 4.3
Comparação dos resultados de relutância, com entre-
ferro de
0, 4 mm. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 185
Tabela 4.4
ferro de
Comparação dos resultados de relutância, com entre-
5 mm. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Tabela 4.5
186
Perdas por massa e volume para diferentes condições
de entreferro . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189
Tabela 4.6
Distribuição da energia nas regiões do sistema, obtidas
por simulação, para entreferro de 0,4 mm. . . . . . . . . . . . . . . . . . . . . . . . 191
Tabela 4.7
Distribuição da energia nas regiões do sistema, obtidas
por simulação, para entreferro de 5 mm. . . . . . . . . . . . . . . . . . . . . . . . . . 192
Tabela 4.8
Triângulo de potência do contactor. . . . . . . . . . . . . . . . . . . 193
Tabela 4.9
Energia acumulada no contactor. . . . . . . . . . . . . . . . . . . . . . 199
Tabela 4.10 Síntese dos resultados obtidos com o Tensor Ponderado
de Maxwell. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201
Tabela 4.11 Resultados da simulação no FEMM. . . . . . . . . . . . . . . . . . . 205
Tabela 4.12 Resultados da simulação no FEMM. . . . . . . . . . . . . . . . . . . 211
LISTA DE ABREVIATURAS E SIGLAS
CA
Corrente Alternada
CAD
Computer Aided Design
CC
Corrente Contínua
CEE
Conversão Eletromecânica de Energia
FEMM
Finite Element Method Magnetics
GNO
Grão Não-Orientado
GO
Grão Orientado
IEC
International Electrotechnical Commission
JA
Jiles-Atherton
MEL
Materiais Elétricos
PWM
Pulse Width Modulation
LISTA DE SÍMBOLOS
a
ai
aJA
B
B0
Bm
Bmax
Bsat
Br
Bs
C
D
d
dB
dH
dif
dl
dt
dx
dφ
E
Ean
Ems
Emt
Et
e
e0
F
FCA
FCC
Fc
FP
Relação de espiras
Coeciente do potencial magnético
Coeciente de JA
Densidade de uxo magnético
Indução máxima de vazio
Indução magnética máxima no material na operação
Indução de saturação máxima
Indução no ponto de saturação
Remanência
Densidade de saturação
Capacitância
Dobro da área do triângulo da malha
Distância das bordas de laminação
Diferencial de indução magnética
Diferencial de campo magnético
Diferencial da corrente de Focault
if
Diferencial de comprimento
Diferencial de tempo
Diferencial da coordenada espacial
x
Diferencial de uxo
Tensão induzida
Energia de anisotropia magnetocristalina
Energia magnetostática
Energia de magnetostricção
Energia de troca
Espessura da lâmina
Espessura inicial da lâmina
Funcional
Força CA
Força CC
Força do contactor
Fator de potência
f
G
g
H
H0
Hc
Hm
h
hp
I
I0 , i0
I1
I1cc
I2
Ie
Inpk
Ix
Iy
if
im
j
K
Kcont
Kexc,B
Kexc,C
Kh
KL1
KL2
kJA
L
L1
L2
LM
Lm
Frequência de operação
Coeciente de atrito
Comprimento do entreferro
Intensidade de campo magnético
Campo magnético máximo de vazio
Coercividade
Campo magnético do ponto nal da curva
BH
Altura da lâmina
Constante de Plank
Corrente
Corrente de vazio
Corrente RMS de primário
Corrente de primário no ensaio de curto circuito
Corrente RMS de secundário
Corrente na espira de sombra
Corrente nominal de pico
Corrente no circuito da Figura 3.53
Corrente no circuito da Figura 3.54
Corrente de Focault
Corrente de magnetização
Unidade imaginária
Fator de acoplamento
Constante de força do contactor
Constante de perdas excedentes de Bertotti
Constante de perdas excedentes de Campos
Constante de perdas por histerese
Constante de indutância do primário
Constante de indutância do secundário
Constante de JA
Indutância própria
Indutância própria do primário
Indutância própria do secundário
Indutância mútua
Indutância de magnetização
l1
l2
lm
M
M12
M21
Mm
Mr
Ms
mB
me
mv
N
N1
N2
Ne
ne
P
P0
P1
Pcu
Pe
Pexc
Pexc,B
Pexc,C
Pf
Ph
Ps
Pt
pi , qi , ri
pm
Q
Q1
qe
Indutância de dispersão do primário
Indutância de dispersão do secundário
Comprimento médio do percurso magnético
Campo de magnetização
Indutância mútua do primário em relação ao secundário
Indutância mútua do secundário em relação ao primário
Magnetização do ponto nal da curva
BH
Magnetização remanente
Magnetização de saturação
Magneton de Bohr
Massa do elétron
Massa especíca do material
Número de espiras
Número de espiras de primário
Número de espiras de secundário
Número de espiras do contactor
Número de elementos da malha
Potencial escalar magnético
Derivada do potencial escalar magnético
Potência ativa do primário
Perdas no cobre
Perda total do modelo
Perdas excedentes
Perdas excedentes de Bertotti
Perdas excedentes de Campos
Perdas por correntes de Focault
Perdas por histerese
Perda simulada
Perdas totais
Coecientes geométricos da malha
Permeância
Vetor de fontes enegéticas do sistema
Potência reativa do primário
Carga do elétron
R
R2
Rc
Req
Rf
Rleq1
Rn
Rp
Rs
Rsh
resp
S
S0
S1
Sf
SR
SS
Um
V
V1
V2
Vcc
Vch1
Vch2
Vn
Vo
Vpk
Vx
Vy
v
W
Wc
We
Wm
Resistência
Resistor de medição do secundário
Resistência equivalente de perdas do núcleo
Resistência equivalente
Resistência elétrica do percurso magnético
Resistência equivalente de primário
Resistência equivalente do núcleo
Resistência do modelo paralelo
Resistência do modelo série
Resistência
shunt
Desempenho magnético
Seção transversal do núcleo
Área corrigida da seção do entreferro
Potência aparente do primário
Área efetiva disponível para o uxo
Matriz de rigidez dos coecientes
Matriz global dos coecientes
Tensão máxima da onda
Potencial elétrico
Tensão RMS de primário
Tensão RMS de secundário
Tensão de primário no ensaio de curto circuito
Tensão do canal 1 do osciloscópio
Tensão do canal 2 do osciloscópio
Tensão nominal ecaz
Campo coercitivo do objeto magnético
Tensão de pico
Tensão do circuito da Figura 3.53
Tensão do circuito da Figura 3.54
Volume
Energia
Energia acumulada no entreferro
Energia elétrica
Energia magnética
Wn
w
Xleq1
Xlp
Xm
Xs
x
x1
x2
y
Z1
Z2
Zx
Zy
αh
αJA
κx
λ
λm
λR
µ
µ0
µabs
µdif
µmax
µr
ν
φ
φm
φp
ρ
ρv
σ
Energia acumulada no núcleo
Densidade de energia
Reatância equivalente de primário
Reatância indutiva do modelo paralelo
Reatância de magnetização
Reatância indutiva do modelo série
Coordenada espacial horizontal
Reatância de dispersão primaria
Reatância de dispersão secundaria
Coordenada espacial vertical
Impedância vista do lado primário
Impedância vista do lado secundário
Impedância do circuito da Figura 3.53
Impedância do circuito da Figura 3.54
Expoente de histerese
Expoente de JA
Permissividade elétrica
Constante que caracteriza o meio material
Fluxo concatenado
Fluxo de pico
Fluxo residual
Permeabilidade magnética
Permeabilidade relativa do vácuo
Permeabilidade absoluta
Permeabilidade diferencial
Máxima permeabilidade magnética relativa
Permeabilidade relativa do material
Relutividade magnética
Fluxo magnético
Fluxo máximo
Potencial da malha
Resistividade elétrica do material
Densidade volumétrica de carga
Condutividade elétrica
θ
χc
χin
χm
χr
Ω
ω
F
<
∆
∇2
|.|
||.||
Defasagem de onda
Susceptibilidade coercitiva
Susceptibilidade inicial
Susceptibilidade do ponto nal da curva
Susceptibilidade remanente
Superfície matemática
Frequência angular
Força magnetomotriz
Relutância
Operador de variação discreta
Operador laplaciano
Notação de módulo
Notação de tensor
BH
SUMÁRIO
1 INTRODUÇÃO
1.1
39
REVISÃO DE LITERATURA
. . . . . . . . . . . . . .
BH
1.1.1
Modelos numéricos no plano
1.1.2
Cálculo de perdas magnéticas em programas de
elementos nitos
. . . . . . . . .
. . . . . . . . . . . . . . . . . .
. . . . . . . . . . . .
39
44
45
1.2
PROPOSTA DA DISSERTAÇÃO
1.3
MOTIVAÇÃO DA DISSERTAÇÃO
. . . . . . . . . . .
46
1.4
ORGANIZAÇÃO DA DISSERTAÇÃO . . . . . . . . . .
46
2 O MÉTODO DOS ELEMENTOS FINITOS
46
47
2.1
POTENCIAIS E MINIMALIDADE ENERGÉTICA
. .
48
2.2
O MÉTODO VARIACIONAL . . . . . . . . . . . . . . .
49
2.3
ELEMENTOS TRIANGULARES DE PRIMEIRA OR-
2.4
2.5
DEM . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
FUNÇÕES INTERPOLANTES DE PRIMEIRO GRAU
52
SISTEMAS INFORMÁTICOS PARA CÁLCULO NUMÉRICO DE CAMPOS ELETROMAGNÉTICOS
2.6
. . .
58
CONSIDERAÇÕES FINAIS DO CAPÍTULO . . . . . .
59
3 CARACTERIZAÇÃO DE UM TRANSFORMADOR
MONOFÁSICO
61
3.1
PERDAS EM MATERIAIS FERROMAGNÉTICOS . .
61
3.1.1
Aços de baixo carbono . . . . . . . . . . . . . . .
62
3.1.2
Aços de grão orientado . . . . . . . . . . . . . . .
64
3.1.3
Materiais ferromagnéticos amorfos (vidros metá-
3.1.4
Momento magnético, magnetização e materiais
3.1.5
Domínios magnéticos (ou, de Weiss): uma ques-
licos) . . . . . . . . . . . . . . . . . . . . . . . . .
magnéticos
. . . . . . . . . . . . . . . . . . . . .
64
66
tão energética . . . . . . . . . . . . . . . . . . . .
68
3.1.5.1
69
Paredes de domínio
. . . . . . . . . . .
3.1.6
Magnetização e susceptância magnética
. . . . .
70
3.1.6.1
. . . . .
73
3.1.7
Modelos de perdas para materiais magnéticos . .
77
3.1.7.1
Curva de magnetização inicial
Perdas por histerese e perdas magnéticas totais . . . . . . . . . . . . . . . . .
77
3.1.7.2
Histerese através da visão de energia
3.1.7.3
Perdas por correntes de Foucault ou pa-
3.1.7.4
Perdas por correntes de Foucault exce-
nos domínios . . . . . . . . . . . . . . .
rasitas . . . . . . . . . . . . . . . . . . .
dentes . . . . . . . . . . . . . . . . . . .
3.1.8
Extensão do modelo de perdas sob regime não
3.1.9
Modelo de Jiles Atherton de histerese magnética
senoidal (PWM)
. . . . . . . . . . . . . . . . . .
e seus parâmetros ótimos
3.2
3.3
3.6
83
86
88
MÉTODOS E EQUIPAMENTOS PARA A CARACTE89
3.3.1
Medidor das perdas de histerese
. . . . . . . . .
89
3.3.2
O quadro de Epstein . . . . . . . . . . . . . . . .
90
3.3.3
Circuito esquemático . . . . . . . . . . . . . . . .
91
3.3.4
O Sensor de lâmina única
91
3.3.5
Técnica para a medição dos processos de orien-
3.3.6
Textura Cristalográca
. . . . . . . . . . . . .
. . . . . . . . . . .
. . . . . . . . . . . . . .
OBTENÇÃO CURVA DE HISTERESE
BH
93
95
. . . . . . . . .
96
. . . . . . . . . . .
101
3.4.1
Pontos notáveis da curva
3.4.2
Obtenção da curva
. . . . . . . . . . . . . .
103
3.4.3
Identicação do material . . . . . . . . . . . . . .
103
BH
CARACTERIZAÇÃO DO MODELO DE JILES-ATHERTOM104
CURVAS DE GRANDEZAS MAGNÉTICAS DO TRANSFORMADOR . . . . . . . . . . . . . . . . . . . . . . . .
106
3.6.1
Curva da permeabilidade magnética diferencial .
106
3.6.2
Permeabilidade magnética do núcleo em função
3.6.3
Indutâncias próprias
3.6.4
Obtenção experimental da indutância primária e
secundária . . . . . . . . . . . . . . . . . . . . . .
111
3.6.5
Cálculo de indutâncias mútuas
. . . . . . . . . .
113
3.6.6
Curva de Relutância . . . . . . . . . . . . . . . .
114
3.6.7
Curva da permeância
115
3.6.8
Considerações sobre a permeabilidade e a curva
da corrente primária . . . . . . . . . . . . . . . .
rente primária
BH
3.7
81
. . . . . . . . . . . . .
tação cristalográca (EBSD)
3.5
79
DISPOSITIVO EM ESTUDO . . . . . . . . . . . . . . .
RIZAÇÃO DE MATERIAIS FERROMAGNÉTICOS . .
3.4
79
L1
e
L2
108
em função da cor-
. . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . .
109
116
CÁLCULO DE INDUTÂNCIAS EM UM PONTO DE
OPERAÇÃO
. . . . . . . . . . . . . . . . . . . . . . . .
116
3.7.1
Cálculo das indutâncias mútuas e reatância de
3.7.2
Cálculo de indutâncias mútuas por energia em
dispersão pelo método concatenado . . . . . . . .
117
buc-
condições de polaridade aditiva e subtrativa (
king test )
3.8
3.9
. . . . . . . . . . . . . . . . . . . . . .
119
3.7.3
Cálculo das indutâncias pelo método gráco . . .
120
3.7.4
Fator de acoplamento
122
. . . . . . . . . . . . . . .
DETERMINAÇÃO EXPERIMENTAL DAS INDUTÂNCIAS MÚTUAS NO PONTO DE OPERAÇÃO . . . . .
123
MODELAGEM DO TRANSFORMADOR . . . . . . . .
125
3.9.1
Cálculo da corrente de vazio (corrente de magne-
3.9.2
Modelagem do núcleo do transformador
3.9.3
Transformação de impedâncias
. . . . . . . . . .
126
3.9.4
Modelo através de ensaios experimentais . . . . .
129
tização)
. . . . . . . . . . . . . . . . . . . . . . .
. . . . .
125
126
3.10 MODELAGEM DAS PERDAS NO TRANSFORMADOR131
3.10.1 Cálculo das resistências primária e secundária do
bobinado
. . . . . . . . . . . . . . . . . . . . . .
133
3.10.2 Obtenção experiemental das perdas resistivas e a
dispersão magnética
. . . . . . . . . . . . . . . .
133
3.10.3 Perdas no ferro . . . . . . . . . . . . . . . . . . .
135
3.10.4 Perdas Totais . . . . . . . . . . . . . . . . . . . .
136
3.11 ENERGIA DISSIPADA NA CURVA DE HISTERESE .
136
3.11.1 Perdas por unidade de massa e volume . . . . . .
139
3.11.2 Potência ativa por unidade de massa . . . . . . .
139
3.11.3 Rendimento máximo . . . . . . . . . . . . . . . .
140
3.11.4 Ponto ótimo de operação
. . . . . . . . . . . . .
140
3.11.5 Triângulo de potências . . . . . . . . . . . . . . .
142
3.12 SEPARAÇÃO DAS PERDAS . . . . . . . . . . . . . . .
142
3.12.1 Perda de histerese
. . . . . . . . . . . . . . . . .
3.12.2 Perdas por correntes parasitas (Foucault)
143
. . . .
143
3.12.3 Perdas excedentes (modelo Bertotti) . . . . . . .
143
3.12.4 Aplicação do modelo de perdas . . . . . . . . . .
143
3.13 CORRENTE DE
IN-RUSH
. . . . . . . . . . . . . . . .
147
Comportamento em regime não-saturado . . . .
147
3.13.2 Comportamento em regime saturado . . . . . . .
150
3.13.3 Características de uma corrente de
152
3.13.1
in-rush . . .
in-rush num
3.13.4 Os principais efeitos das correntes de
sistema
. . . . . . . . . . . . . . . . . . . . . . .
3.13.5 A intensidade e a duração das correntes de
153
in-rush 153
3.13.6 Modelo de transformador monofásico . . . . . . .
154
3.13.7 Representação da histerese
3.13.8 Curva
BH
. . . . . . . . . . . .
do material ferromagnético do núcleo
3.13.9 Resultados experimentais
154
155
. . . . . . . . . . . . .
155
3.13.10 Resultados das simulações . . . . . . . . . . . . .
156
3.13.11 Considerações sobre os resultados do modelo para
a corrente de
in-rush
. . . . . . . . . . . . . . . .
160
3.14 CONSIDERAÇÕES FINAIS DO CAPÍTULO . . . . . .
160
4 CARACTERIZAÇÃO DE UM CONTACTOR CA
4.1
OBJETIVOS
4.2
DESCRIÇÃO DO PROBLEMA
165
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . .
4.2.1
Determinação experimental do número de espiras
4.2.2
Tensão e corrente experimentais na espira de som-
da bobina . . . . . . . . . . . . . . . . . . . . . .
bra . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3
165
166
168
171
DETERMINAÇÃO DAS CARACTERÍSTICAS MAGNÉTICAS DO NÚCLEO
. . . . . . . . . . . . . . . . .
174
4.3.1
Circuito proposto para levantar a curva de histerese176
4.3.2
Fatores de escala . . . . . . . . . . . . . . . . . .
4.3.3
Formas de onda da tensão (B ) e corrente (H ) em
4.3.4
Curva de histerese
4.3.5
Curva de saturação magnética
4.3.6
Curva da permeabilidade magnética relativa
função do tempo
. . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .
BH
em função da intensidade de campo
. . . . . . . .
176
177
177
178
µr
. . . . . . .
179
4.3.7
Obtenção gráca da permeabilidade absoluta no
4.3.8
Determinação da Relutância do Contactor . . . .
182
4.3.9
Determinação da Curva de Permeância
186
ponto de operação para a condição entreferro 0,4mm181
4.4
. . . . .
SIMULAÇÕES DO DISPOSITIVO UTILIZANDO A CURVA
BH
EXPERIEMENTAL
. . . . . . . . . . . . . . . . .
4.4.1
Determinação da corrente na espira de sombra
4.4.2
Determinação da energia dissipada no ciclo de
4.4.3
4.4.4
Análise energética do contactor a partir da curva
4.4.5
Triângulo de potência
4.4.6
Energia e força nos entreferros
186
.
187
histerese . . . . . . . . . . . . . . . . . . . . . . .
188
Perdas no dispositivo . . . . . . . . . . . . . . . .
189
BH
. . . . . . . . . . . . . . . . . . . . . . . . .
4.4.6.1
. . . . . . . . . . . . . . .
. . . . . . . . . .
189
192
194
Método gráco através da curva BH da
energia acumulada no entreferro de
0, 4 mm 196
4.4.6.2
Método gráco através da curva BH da
4.4.6.3
Método das energias nos entreferros
4.4.6.4
Método da densidade de força (pressão
magnética) . . . . . . . . . . . . . . . .
200
4.4.6.5
Método dos elementos nitos . . . . . .
200
4.4.6.6
Comparação dos métodos de cálculo de
energia acumulada no entreferro de
força
5 mm 197
. .
. . . . . . . . . . . . . . . . . . .
4.5
MODELAGEM ELÉTRICA DO DISPOSITIVO
4.6
EFEITOS DO ENTREFERRO NO PROJETO DE DIS-
4.7
. . . .
204
207
CONSIDERAÇÕES FINAIS DO CAPÍTULO . . . . . .
209
213
PUBLICAÇÕES GERADAS AO LONGO DESSE TRABALHO . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2
201
POSITIVOS ELETROMAGNÉTICOS . . . . . . . . . .
5 CONSIDERAÇÕES FINAIS
5.1
198
214
PERSPECTIVAS DE EVOLUÇÃO DA METODOLOGIA215
REFERÊNCIAS BIBLIOGRÁFICAS
217
ANEXO A -- LAÇO DE HISTERESE MAGNÉTICA FUNDAMENTAÇÃO TEÓRICA
223
ANEXO B -- MODELO DE JILES E ATHERTOM
229
ANEXO C -- METODOLOGIA DE CONSTRUÇÃO DE
UM TRANSFORMADOR MONOFÁSICO
235
ANEXO D -- FORMAS DE ONDA
241
ANEXO E -- ARTIGOS DESENVOLVIDOS AO LONGO
DO TRABALHO
245
ANEXO F -- PROGRAMAÇÃO EM LUA
247
ANEXO G -- MODELOS DE PERDAS EXCEDENTES
DE BERTOTTI E CONCEITO DE OBJETO MAGNÉTICO (OM)
251
39
1 INTRODUÇÃO
O estudo de transformadores e outros dispositivos remontam ao
início das pesquisas em fenômenos magnéticos e, ainda hoje, são alvo de
inúmeros estudos. Desse modo, nessa introdução, é realizada uma breve
revisão de literatura a respeito dos fenômenos eletromagnéticos envolvendo transformadores e outros dispositivos eletromagnéticos. Adicionalmente, são apresentadas a proposta dessa dissertação e a motivação
do trabalho e, por m, a organização geral de todo o estudo desenvolvido.
1.1 REVISÃO DE LITERATURA
Transformadores e reatores são dispositivos cujas respostas a
uma dada excitação dependem da frequência de operação e de fenômenos não lineares.
O comportamento não linear do núcleo desses
dispositivos se deve a fenômenos associados aos materiais ferromagnéticos como saturação e histerese magnética. Por outro lado, os efeitos
associados à frequência de operação são causados por correntes induzidas nas laminações, conhecidas como correntes parasitas ou correntes
de Foucault. O modelamento teórico completo do núcleo deve incluir
o efeito das não linearidades e a inuência da frequência.
Esses mo-
delos são importantes no estudo de fenômenos como ferrorressonância,
correntes transitórias de magnetização, bem como na estimativa das
perdas irreversíveis de energia sob a forma de calor (SAY, 1983). As
técnicas numéricas para análise dos fenômenos não lineares presentes
nos materiais ferromagnéticos são, até hoje, objeto de muitas pesquisas
e publicações que incluem uma detalhada fundamentação teórica bem
como inúmeras aplicações voltadas para o desenvolvimento de projetos e construção de equipamentos elétricos (SILVESTER; FERRARI,
1990; NOGUEIRA; PEREIRA JR, 2006).
As técnicas para inclusão dos efeitos das correntes parasitas são
baseadas na solução da equação de difusão de correntes utilizando técnicas numéricas como diferenças nitas ou elementos nitos (STOLL,
1974). A inclusão da histerese magnética, por outro lado, requer um
tratamento bem mais elaborado. Os modelos baseados no alinhamento
40
de domínios magnéticos descrevem de forma clara o fenômeno da histerese, mas a incorporação das previsões teóricas desses métodos às
técnicas de análise de dispositivos ferromagnéticos resulta, quase sempre, em problemas numéricos de precisão e consistência de dados.
Para explicar o fenômeno da histerese na condição estática ou
quase-estática, pode-se considerar o comportamento do núcleo ferromagnético de um reator ou de um transformador operando em vazio.
Quando o enrolamento primário de um transformador é energizado por
uma fonte de corrente ajustada de forma que a corrente magnetizante
varia entre
os campos
+im e −im e retorna para o
B e H é representada por uma
cida como laço de histerese.
im
valor
+im ,
a relação entre
característica cíclica conhe-
Para valores da corrente magnetizante
sucientemente elevados para levar o núcleo à saturação, os pontos
de operação no plano
BH
seguem o laço mais externo da ilustração
apresentada na Figura 1.1 que representa o limite dessa condição de
operação. Quando a amplitude da corrente magnetizante máxima im é
menor, laços menores, também simétricos em relação à origem do plano
BH ,
são gerados. A ilustração da Figura 1.1 também mostra a curva
normal de magnetização traçada a partir da origem do plano
obtida a partir da união dos vértices dos laços concêntricos.
Figura 1.1 Laços de histerese, operação quase-estática.
Fonte: Adaptado de (NOGUEIRA; PEREIRA JR, 2006).
BH
e
41
Na operação em vazio, quando somente um enrolamento de um
transformador é alimentado por uma fonte alternada, o processo de
magnetização do núcleo passa a ser não uniforme devido à presença
das correntes parasitas. O campo magnético criado por essas correntes
se opõe ao campo magnetizante e, como consequência, a dissipação
de calor é menor nas regiões mais próximas do centro geométrico das
laminações. Nas regiões mais próximas às superfícies da laminação a
dissipação de calor é maior devido à maior intensidade e concentração
de correntes induzidas. A Figura 1.2 ilustra o processo de decaimento
da intensidade de campo magnético resultante
de espessura
d
H
em uma laminação
em função da distância até as bordas da laminação.
Figura 1.2 Intensidade de campo
H
em uma laminação de espessura
d.
Fonte: Adaptado de (NOGUEIRA; PEREIRA JR, 2006).
A discussão acima ilustra o grau de complexidade envolvido no
desenvolvimento de modelos matemáticos para representar o funcionamento magneto-dinâmico de estruturas magnéticas laminadas. Um
modelo preciso deve contemplar, simultaneamente, o fenômeno da histerese, que é não linear e independente da frequência e o fenômeno
das correntes parasitas induzidas, que é magneticamente linear, mas
42
dependente da frequência. Os grácos apresentados nas Figuras 1.3 e
1.4 foram obtidos por (FÜZI, 1999) em seu trabalho com laminações
de grãos orientados 27ZDKH95 com espessura de
0, 27 mm.
Os grá-
cos representam resultados da operação nas frequências de 50 e 250
hertz, respectivamente.
Cada gráco contém quatro diferentes laços,
concêntricos em torno da origem do plano
BH .
Cada laço representa
os resultados de um procedimento diferente: medição experimental do
laço de histerese na frequência de 1 hertz, ou seja, operação quase estática (
st.), medição experimental das perdas totais (meas.), simulação
eddy c.) e simulação computaciocomportamento dinâmico (comp ). Ambos os grácos contêm
de perdas por correntes parasitas (
nal do
os resultados dos procedimentos associados à direção preferencial de
magnetização da laminação.
Figura 1.3 Laços de histerese,
f = 50 Hz.
Fonte: Adaptado de (FÜZI, 1999).
43
Figura 1.4 Laços de histerese,
f = 250 Hz.
Fonte: Adaptado de (FÜZI, 1999).
Deve-se ressaltar que, em ambos os grácos, o mesmo laço repre-
st.), na frequên-
senta a histerese magnética da operação quase estática (
cia de 1 hertz. Observar, ainda, o aumento substancial na área do laço
eddy c.)
associado às perdas por correntes parasitas (
em decorrência do
aumento da frequência, o que está em consonância com o entendimento
físico do problema. Para ambas as condições de operação, observa-se
que o modelo computacional gera ótimas estimativas dos valores obtidos a partir das medições em laboratório, essas últimas realizadas
utilizando-se o sistema de medidas magnéticas descrito por (PFÜTZNER; SCHÖNHUBER, 1991).
44
1.1.1 Modelos numéricos no plano BH
A literatura registra várias técnicas de medição de grandezas
elétricas e magnéticas que permitem uma análise rápida e precisa das
características dos materiais magnéticos a partir das bases físicas da relação entre a densidade de uxo magnético
magnético
H.
B
e a intensidade de campo
Para contornar as diculdades associadas à não linea-
ridade da relação entre os campos
B
e
H,
vários modelos numéricos
aproximados, linearizados, têm sido propostos.
Tais modelos usual-
mente conduzem a previsões rápidas e úteis sobre o comportamento
dos dispositivos em estudo, através de cálculos mais simples e de fácil
entendimento. Os modelos matemáticos mais simples produzem características monotonamente crescentes e univalentes, como a característica apresentada na Figura 1.5. Alguns modelos, formados por segmentos lineares, são aproximações simplicadas de características como a
curva inicial de magnetização que pode ser medida experimentalmente.
O procedimento para medição das curvas iniciais de magnetização de
materiais ferromagnéticos é descrito na norma técnica IEC 60404-4.
Existem também os modelos matemáticos, linearizados ou não, que
preservam o efeito da histerese magnética. Tais modelos são essenciais no estudo de equipamentos como máquinas de ímã permanente e
amplicadores magnéticos (OSSART; MEUNIER, 1990).
Diferentes modelos numéricos para o fenômeno da histerese magnética têm sido propostos.
Tais modelos reetem, no plano
BH ,
de
forma aproximada, fenômenos físicos de alta complexidade como magnetização reversível, magnetização irreversível, laços menores, efeitos
dinâmicos e efeitos da temperatura (MAZAURIC et al., 2005; JILES D.
C.; ATHERTON, 1983). Um dos primeiros modelos matemáticos para
o fenômeno de histerese magnética foi proposto, já em 1935, por Preisach (PREISACH, 1935). As características e aplicações dos modelos
para a histerese quase estática propostos por Preisach, Globus, StonerWolhfarth e Jiles-Atherton foram comparadas por Liorzou, Phelps e
Atherton (2000), levando em consideração vários aspectos, tais como:
mecanismos de movimentação das paredes dos domínios, anisotropia,
textura, reversibilidade, desmagnetização, parâmetros mensuráveis, domínios dos grãos, bem como o tipo de material da amostra: magneticamente duro, mole ou intermediário (LIORZOU; PHELPS; ATHERTON, 2000).
45
Figura 1.5 Característica de magnetização, linearizada por partes.
Fonte: produção do autor.
1.1.2 Cálculo de perdas magnéticas em programas de elementos nitos
Uma importante contribuição para o estado da arte é a incorporação da modelagem dos fenômenos de histerese e correntes parasitas
em programas de simulação baseados na técnica de elementos nitos.
É o que ocorreu com a suíte de programas gratuitos conhecida popularmente como FEMM (MEEKER, 2015) e com o módulo para análise de
problemas harmônicos da suíte de programas da Infolytica Corporation
(INFOLYTICA, 2006).
46
Um trabalho de pesquisa elementar voltado para a escolha e implementação de um procedimento experimental para aquisição e análise
do laço de histerese do núcleo de contactores e transformadores de baixa
potência é descrito nas seções que se seguem.
1.2 PROPOSTA DA DISSERTAÇÃO
Este trabalho apresenta uma metodologia simples para avaliar as
características magnéticas dos materiais, utilizando um circuito
RC
e
equipamentos usuais de um laboratório de máquinas elétricas. Com esses equipamentos é possível obter as curvas de histerese e de saturação
magnética
BH .
A partir destas curvas e com a teoria eletromagnética,
é possível determinar os parâmetros elétricos de um dispositivo, como
perdas e eciência energética, fornecendo uma visão qualitativa e auxiliando a compreensão compreensão de fenômenos eletromagnéticos no
projeto de máquinas elétricas e transformadores.
1.3 MOTIVAÇÃO DA DISSERTAÇÃO
A necessidade de apresentar uma visão qualitativa e prática de
dispositivos abordados nos laboratórios das disciplinas de conversão eletromecânica de energia (CEE) e de materiais elétricos (MEL), servindo
de apoio nas práticas pedagógicas destas disciplinas.
1.4 ORGANIZAÇÃO DA DISSERTAÇÃO
No Capítulo 2, são apresentados os fundamentos teóricos do método dos elementos nitos, que foi a principal ferramenta de simulação
utilizada em todo o trabalho. No Capítulo 3, apresenta-se um estudo
da caracterização de um transformador monofásico, determinando-se
características de seu material e seus parâmetros eletromagnéticos, a
partir de sua curva de histerese. No Capítulo 4, é apresentada a caracterização de um dispositivo eletromagnético com entreferro variável, o
contactor, aplicando-se as mesmas técnicas desenvolvidas no Capítulo
3. Por m, no Capítulo 5 são apresentadas as conclusões e as considerações nais desse trabalho dissertativo, além de propostas para possíveis
trabalhos futuros.
47
2 O MÉTODO DOS
ELEMENTOS FINITOS
O método dos elementos nitos é baseado na ideia de dividir o
domínio original do problema, o
continuum, em um conjunto de domí-
nios menores conhecidos como elementos. Uma formulação numérica,
baseada na teoria das interpolações, é aplicada a esses elementos de
forma a satisfazer a uma condição matemática e produzir uma solução
numérica. Trata-se de uma técnica numérica para a solução, em grande
escala, de problemas de alta complexidade utilizando uma estrutura de
dados que é, ao mesmo tempo, simples e exível (NOGUEIRA; BOUDEC, 2007).
Os elementos nitos são denidos com base em sua forma geométrica e no grau da função de aproximação. Essa função é, na maioria dos
casos, polinomial e dene a forma como a variável primária de cálculo,
usualmente um potencial, comporta-se no minúsculo espaço delimitado
por cada elemento nito.
Muitas formas geométricas podem ser uti-
lizadas em uma análise bidimensional; o elemento triangular é o mais
usado.
Na maioria das aplicações, funções interpolantes de primeiro
grau são sucientes para atender ao compromisso entre a precisão numérica requerida e as demandas em termos de esforço computacional e
tempo de processamento (BASTOS, 1992).
Na era moderna, o método dos elementos nitos foi aplicado inicialmente para resolver problemas de análise estrutural e, já nos anos
1950, o método foi empregado na solução de problemas de transferência de calor e escoamento de uidos.
Em 1970, um artigo de Silves-
ter e Chari intitulado solução por elementos nitos de problemas de
campos magnéticos envolvendo saturação (no inglês,
lution of saturable magnetic eld problems )
nite element so-
abriu uma nova Era para
o eletromagnetismo (SILVESTER; CHARI, 1970). Naquele trabalho,
foram apresentados os detalhes da utilização conjunta da técnica dos
elementos nitos com o método variacional. A formulação matemática
apresentada formou a base de cálculo dos primeiros sistemas informáticos para o cálculo numérico de campos eletromagnéticos. Silvester e
Chari (1970) forneceram contribuições de forma decisiva para o desenvolvimento dessa técnica amplamente utilizada na engenharia elétrica.
48
2.1 POTENCIAIS E MINIMALIDADE ENERGÉTICA
A análise de campos eletromagnéticos é, algumas vezes, facilitada quando, ao invés de campos vetoriais, uma distribuição de potenciais é utilizada como grandeza primária da análise.
As equações de
Poisson e Laplace, expressas em termos de potenciais, podem ser derivadas das equações de Maxwell e resolvidas sob determinadas condições
de contorno também especicadas em termos de potenciais (HAMDI;
NOGUEIRA; SILVESTER, 1993).
As equações de Poisson e Laplace são exemplos de equações diferenciais parciais que, respectivamente, descrevem problemas eletrostáticos e magnetostáticos.
A equação de Poisson pode ser expressa
como
∇2 V =
onde
V
ρ
é o potencial eletrostático,
ρv
(2.1)
a densidade de carga elétrica e
é a permissividade elétrica do meio material.
A equação de Laplace pode ser expressa como
∇2 P = 0
onde
P
é o potencial escalar magnéticoe
(2.2)
∇2
é o operador laplaciano.
Em problemas eletrostáticos e magnetostáticos, as energias armazenadas, elétrica
We
e magnética
Wm ,
respectivamente, podem ser
expressas em termos de potenciais,
2
Z
µ
=
2
Z
We =
e
Wm
(∇V )2 dv
(2.3)
(∇P )2 dv.
(2.4)
v
v
É importante observar que ambas as energias são expressas em
termos de valores quadráticos do gradiente de campo, uma característica que pode ser explorada para obter soluções numéricas. É importante ressaltar que existem muitos sistemas físicos nos quais o processo
de minimização da energia potencial do sistema conduz à solução numérica do problema. Em outras palavras, a solução numérica consiste
de uma distribuição de potenciais associados a um mínimo local e não
trivial da função composta que dene a energia potencial do sistema.
49
Os potenciais que aparecem nas equações (2.3) e (2.4) são função
da posição. Em problemas bidimensionais denidos no plano
x − y , por
exemplo, esses potenciais podem ser expressos como:
V = V (x, y),
(2.5)
P = P (x, y).
(2.6)
A energia associada a cada distribuição de potencial é, pois, uma
função dos potenciais os quais, por sua vez, são dependentes da posição.
A energia é, portanto, representada por uma função composta
conhecida como funcional energético (SILVESTER; FERRARI, 1990).
2.2 O MÉTODO VARIACIONAL
A implementação da técnica de elementos nitos é normalmente
feita em conjunto com métodos matemáticos como o método variacional
e o método dos resíduos ponderados. Quando o método variacional é
aplicado para obter a solução de uma equação diferencial parcial que
descreve um problema de campo, a solução para a equação diferencial
é obtida de forma indireta. No caso, dene-se um funcional energético,
que é expresso como uma integral de volume de uma função denida
em termos das variáveis dependentes do problema original. Para uma
dada função
P
com derivadas parciais
Px0 , Py0
e
Pz0 ,
o funcional
F
é
expresso como
Z
F =
f (P, Px0 , Py0 , Pz0 )dv
(2.7)
v
onde
Px0 =
∂P
∂x ;
Py0 =
∂P
∂y
; Pz0 =
∂P
∂z
(2.8)
O processo de solução consiste na busca de uma função multivariável
P
para a qual o funcional energético
F
é estacionário. Para
obter a solução através dessa abordagem, o funcional
maneira que o integrando
Euler:
f
F
é denido de
da equação (2.7) satisfaça à equação de
∂f
∂ ∂f
∂ ∂f
∂ ∂f
−
−
−
=0
0
0
∂P
∂x ∂x
∂y ∂y
∂z ∂z 0
(2.9)
50
onde o problema original está sujeito a condições de contorno na fronteira
teira
Ω
Ω
que delimita a região ou domínio de análise. Em geral, a fronpode ser denida como a união de duas superfícies:
Ω = ΩD ∪ ΩN
(2.10)
ΩD , especica-se um valor constante para a função
∂P é nula. Esse tipo de condição de contorno
é conhecido como condição de Dirichlet. Na superfície ΩN , as condições
de fronteira são relacionadas à derivada da função P em relação ao vetor
unitário n perpendicular ou normal aos pontos da superfície. Quando se
especica derivada normal nula ao longo da superfície ΩN , a condição
Na superfície
P
e, portanto, a variação
de contorno é chamada de condição de Neumann homogênea.
Essa
condição de contorno é também conhecida como condição de contorno
natural. Isso porque as funções
F (P )
P
sem restrições que tornam o funcional
estacionário próximo da solução do problema, automaticamente
satisfazem à restrição de derivada normal nula na superfície
A obtenção de um funcional
F
ΩN .
que é estacionário no entorno da
solução e que satisfaz às condições de contorno do problema requer considerações sobre a natureza, escalar ou vetorial, da variável dependente,
bem como considerações relativas à não linearidade do problema. Funcionais para potenciais escalares e vetoriais em problemas eletrostáticos
e magnetostáticos são documentados em (BASTOS, 1992). Para cada
potencial considerado, é apresentada a dedução/desenvolvimento da
equação de Euler correspondente, bem como uma análise das condições
de contorno. CARDOSO (1995) também registra algumas formulações
variacionais e apresenta uma série de funcionais estacionários obtidos
em termos de campos vetoriais.
2.3 ELEMENTOS TRIANGULARES DE PRIMEIRA ORDEM
Para aplicar a técnica de elementos nitos, é necessário subdividir a região do problema em sub-regiões chamadas de elementos nitos.
Essa subdivisão (discretização) é feita de modo que um mesmo elemento
não pode conter mais que um meio material. O conjunto de elementos
é conhecido como malha de elementos nitos e, em princípio, não existem restrições para o tamanho e orientação dos elementos. O elemento
triangular de primeira ordem foi escolhido para esta discussão introdutória. Esse tipo de elemento é o mais usado na ciência e engenharia, e é
51
comumente empregado na apresentação dos princípios envolvidos pela
técnica dos elementos nitos.
Quando elementos triangulares de primeira ordem são usados,
todos os pontos nodais ou simplesmente "nós" da malha devem
coincidir com os vértices dos triângulos. Essa restrição é ilustrada com
auxílio da Figura 2.1. Observa-se na Figura 2.1(a) uma malha incorreta
em que um dos pontos nodais não coincide com um vértice de triângulo.
Figura 2.1 Malhas formadas por elementos triangulares de primeira
ordem; (a) malha incorreta; (b) malha correta.
Fonte: produção do autor.
O elemento triangular de primeira ordem também é conhecido
como triângulo com três nós. Outros elementos triangulares também
podem ser usados. É o caso do elemento triangular de segunda ordem,
um elemento triangular que possui seis nós ou pontos nodais. No caso,
três nós coincidem com os vértices e os outros três nós estão localizados
na metade das arestas. No caso, a construção da malha propriamente
dita é feita empregando-se triângulos com três nós.
Os três nós de
arestas são, na verdade, parte da denição da função interpolante quadrática empregada na solução do problema. Elementos nitos de ordem
superior são usados para se obter soluções mais precisas. Entretanto,
elementos triangulares de primeira ordem, desde que adequadamente
usados, conduzem a excelentes resultados e apresentam vantagens em
termos de custo computacional.
52
2.4 FUNÇÕES INTERPOLANTES DE PRIMEIRO GRAU
A maioria das formulações de elementos nitos são baseadas em
potenciais. Para elementos triangulares de primeira ordem, o potencial
φp
varia linearmente dentro do elemento, ou seja,
φp (x, y) = a1 + a2 x + a3 y.
Considere-se um triângulo no plano
x−y
(2.11)
no qual os vértices são
numerados como 1, 2 e 3. Se o potencial nesses vértices assume valores
φ1 , φ2
e
φ3 ,
respectivamente, a equação (2.11) pode ser aplicada em
cada um dos três vértices, resultando em:
φp,1 (x, y) = a1 + a2 x1 + a3 y1 ,
φp,2 (x, y) = a1 + a2 x2 + a3 y2 ,
(2.12)
φp,3 (x, y) = a1 + a2 x3 + a3 y3 .
A solução desse sistema de equações simultâneas fornece os valores dos coecientes
a1 , a2
e
a3
em termos da localização dos vértices
e dos valores dos potenciais.
Para se obter uma expressão que fornece o valor do potencial
φp
em uma localização genérica (x,y ) do elemento triangular, deve-se
substituir os coecientes
a1 , a2
e
a3
na equação 2.11. Após algumas
manipulações algébricas, obtém-se a seguinte expressão:
φp (x, y) =
Na equação 2.13,
D
3
1 X
(pi + qi x + ri y)φi .
D i=1
(2.13)
é igual ao dobro da área do elemento trian-
gular, e os coecientes geométricos
pi , qi
e
ri
são expressos em termos
das coordenadas dos três vértices, como segue:
p1 = x2 y3 − y2 x3 ,
q1 = y2 − y3,
r1 = x3 − x2 ,
(2.14)
p2 = x3 y1 − y3 x1 ,
q2 = y3 − y1,
r2 = x1 − x3 ,
(2.15)
p3 = x1 y2 − y1 x2 ,
q3 = y1 − y2,
r3 = x2 − x1 ,
(2.16)
Vale observar na equação (2.13) que a expressão entre parênteses
(pi
+ qi x + ri y ) representa
uma função planar. É possível, pois, expres-
53
sar o potencial de uma forma mais compacta e de fácil interpretação.
Primeiramente, são denidas as funções de forma,
αi (x, y) =
α,
como a seguir:
1
(pi + qi x + ri y).
D
(2.17)
A expressão para o potencial pode agora ser escrita como
φ(x, y) =
3
X
αi φi .
(2.18)
i=1
Essa forma compacta da expressão facilita a ilustração do processo de cálculo de valores da distribuição de potenciais. Cada função
de forma
α
é nula em dois vértices e possui valor unitário no vértice
restante, como ilustrado nas Figuras 2.2 e 2.3.
A equação (2.18) fornece o potencial dentro de um dado elemento
triangular e é válida para todos os elementos triangulares de uma dada
malha. Vale ressaltar que o potencial ao longo de uma dada aresta é
obtido através de um processo de interpolação linear entre os potenciais dos dois vértices que delimitam a aresta. Quando dois triângulos
compartilham dois vértices (e a aresta correspondente), o potencial será
contínuo ao longo da aresta que representa a fronteira entre esses elementos.
Figura 2.2 Funções planares
αi (x, y).
Fonte: produção do autor
Para um dado problema denido e discretizado no plano
x − y,
com a variação do potencial nos elementos triangulares descrita pela
equação (2.18), o comportamento global do problema pode ser estabelecido pela aplicação de um método variacional. Nessa abordagem, o
funcional energético do problema,
F,
é aproximado pelo somatório dos
54
Figura 2.3 Funções planares
(a) Função α1 (x, y)
(b) Função α2 (x, y)
(c) Função α3 (x, y)
Fonte: Produção do Autor.
funcionais energéticos dos elementos individuais,
a seguir:
F =
ne
X
Fi ,
como apresentado
Fi
(2.19)
i=1
onde
ne
é o número de elementos da malha de elementos nitos.
Para se obter uma solução aproximada para o problema, o funcional
F
é minimizado em relação aos potenciais sem restrições.
55
F , expresso pela equação (2.19),
φk e igualando a zero, tem-se:
Diferenciando o funcional
relação a um potencial genérico
em
n
e
X
∂Fi
∂F
=
=0
∂φp,k
∂φ
p,k
i=1
onde
k
(2.20)
segue a numeração global dos nós com potenciais sem restrição.
Vale observar na equação (2.20) que o somatório engloba todos
os elementos da malha. O valor de cada funcional individual,
nulo no elemento
i
Fi ,
é não
e é igual a zero em todos os outros elementos. No
somatório expresso pela equação (2.20), a contribuição de um determinado nó sem restrição se limita aos funcionais individuais dos elementos
que compartilham aquele nó. No caso simples ilustrado na Figura 2.4,
a contribuição para o somatório da equação (2.20) devido ao nó a que
aparece no centro da malha é
∂F
∂F1
∂F2
∂F3
∂F4
=
+
+
+
∂φp,a
∂φp,a
∂φp,a
∂φp,a
∂φp,a
(2.21)
Figura 2.4 Os elementos 1, 2, 3 e 4 compartilham o nó a.
Fonte: produção do autor.
A minimização do funcional
F
conduz a um conjunto de equações
simultâneas que pode ser expresso em forma matricial. Os funcionais
são diferentes para cada classe de problema. Para problemas magnetostáticos, por exemplo, a denição do funcional deve levar em conta a
56
não linearidade magnética, bem como a presença de correntes elétricas
e ímãs permanentes.
A contribuição de um dado elemento
j
para o
somatório presente na equação (2.20) é:
∂Fj
∂φ1
∂Fj
∂φ2
∂Fj
∂φ3





S11
 
 = S21
S31
S12
S22
S32

 

S13
φp,1
Q1
S23   φp,2  +  Q2 
S33
φp,3
Q3
(2.22)
onde os nós são numerados localmente como 1, 2 e 3.
Na denição da equação matricial expressa pela equação (2.22),
os vértices do elemento triangular
2 e 3. A matriz quadrada
SX(3×3)
j
são identicados pelos números 1,
é conhecida como matriz de rigidez,
uma terminologia herdada da análise estrutural. O termo genérico
Smn
é expresso em termos da área do elemento, dos coecientes geométricos
do elemento e do parâmetro
SXmn =
κx
2D (qm qn
O parâmetro
κ
κx
que caracteriza o meio material,
+ rm rn ) m = 1, 2, 3
n = 1, 2, 3.
(2.23)
representa, por exemplo, a permissividade elé-
trica em problemas eletrostáticos, e a relutividade magnética (inverso
da permeabilidade magnética) em problemas magnetostáticos. O vetor
Q(3×1)
contém informações relativas às fontes energéticas do sistema
físico. Em problemas eletrostáticos, a
m-ésima posição do vetor Q(3×1)
m-ésimo nó.
contém o valor do potencial elétrico especicado para o
Em problemas eletrostáticos, magnetostáticos e magnetodinâmicos as
fontes de energia devem representar os efeitos de cargas elétricas, correntes nodais e ímãs permanentes.
O sistema global que representa as contribuições de todos os n
nós da região discretizada é expresso pela seguinte equação matricial:
SS(m×n) φ(n) = Q(n) .
A matriz
SS(m×n)
(2.24)
SS(m×n) é a matriz global dos coecientes.
Q(3×1) são formados de acordo com os
e o vetor
A matriz
seguintes
procedimentos:
1. para cada elemento
i,
a sua contribuição, expressa pela equação
(2.22), deve ser inserida na matriz
SS
e no vetor
Q
obedecendo
à numeração global dos nós;
2. as restrições de Dirichlet também devem ser inseridas na equação
matricial.
φm ,
a
m tem um
SS terá valor
Se o potencial do nó
m-ésima
linha da matriz
va1or especicado,
unitário na posição
57
mm, e zeros
m-ésima posição do
diagonal,
em todas as posições restantes. Também,
a
vetor
Q
assume o valor
φm ,
especicado
para o potencial daquele nó.
As matrizes de rigidez
SX(3×3)
representam as contribuições dos
elementos individuais e são simétricas na maioria dos casos. O termo
genérico, expresso pela equação (2.23), mostra que a simetria é garantida se o problema é estacionário.
Em certas classes de problemas,
incluindo aqueles que representam corpos em movimento, as matrizes
de rigidez não são simétricas. Em muitos problemas, a matriz global
de coecientes
e de faixa.
SS(m×n)
tem as propriedades de ser simétrica, esparsa
Essas propriedades são extremamente importantes, pois
permitem a utilização de técnicas avançadas de armazenamento e manipulação de matrizes.
Com respeito ao parâmetro
κ que aparece na equação (2.23), vale
e a con-
ressaltar que, na maioria dos casos, a permissividade elétrica
dutividade elétrica
magnética
µ
σ
são constantes. Por outro lado, a permeabilidade
(ou relutividade magnética
ν)
de materiais ferromagné-
ticos é representada pela característica de magnetização que é, quase
sempre, não-linear. Nas regiões ocupadas por meios magnéticos o valor
de
ν
(or
µ)
em cada elemento triangular é função da intensidade de
campo magnético
H,
ν = ν(H).
No caso, a relação entre os campos
(2.25)
B
e
H
é representada mate-
maticamente por
B = kµ(H)kH,
em que a notação
k.k
(2.26)
indica, além da não-lineariadade da dependência
do campo, um possível caráter tensorial de
µ(H), devido a propriedades
anisotrópicas do material ferromagnético.
Surge assim, a necessidade de empregar um processo iterativo
tal como o método das aproximações sucessivas (BASTOS, 1992; SILVESTER; FERRARI, 1990).
O problema restante consiste na solução do sistema de equações
lineares expresso pela equação (2.24) para obter o valor do potencial nos
diversos nós da malha. Muitos métodos numéricos podem ser empregados e esses incluem métodos diretos e iterativos. Existe uma extensa
literatura sobre o assunto (BASTOS, 1992; SILVESTER; FERRARI,
1990).
58
2.5 SISTEMAS INFORMÁTICOS PARA CÁLCULO NUMÉRICO DE CAMPOS ELETROMAGNÉTICOS
A utilização da técnica de elementos nitos para resolver, numericamente, as equações de campo eletromagnético é, hoje em dia,
realizada por programas de propósito geral que são rápidos e de implementação robusta. Existe, na realidade, grande interesse no desenvolvimento de sistemas gerais, em vez de programas orientados para um
problema especíco.
Estes sistemas são conhecidos como sistemas CAD para com-
CAD é a abreviatura de Computer Aided
Design, uma terminologia que realça a importância destes sistemas nos
putação eletromagnética.
projetos de equipamentos eletromagnéticos.
Os três principais fatores que contribuíram para o desenvolvimento destes sistemas foram:
1. o advento do computador digital;
2. o desenvolvimento de computação gráca interativa;
3. os avanços na análise numérica, permitindo que tanto a geometria quanto as equações diferenciais parciais do eletromagnetismo
possam ser tratadas de uma forma discretizada.
É possível analisar um número de diferentes geometrias e as condições de funcionamento, sem a necessidade de construção de um protótipo físico. Além disso, a simulação numérica proporciona, na maioria
dos casos, informações conáveis e precisas sobre comportamento, independentemente da geometria do dispositivo e da complexidade dos
materiais não lineares empregados na construção do mesmo.
Ambientes de
software
modernos que podem ser classicados
como sistemas CAD para solução de problemas eletromagnéticos contêm três elementos principais, que têm acesso a uma base comum de
dados (SILVESTER; FERRARI, 1990):
1. O pré-processador. Permite que o usuário dena a geometria, as
condições de contorno e as fontes de energia. A geração da malha
é também uma operação de pré-processamento;
2. O processador. É o programa para montagem e solução do sistema de equações. A solução, em geral, é apresentada como um
conjunto de potenciais nos pontos nodais.
59
3. O pós-processador.
Permite a visualização e manipulação dos
dados. Trata-se de etapa altamente interativa onde são calculados
parâmetros como forças, indutâncias e perdas.
Existem hoje inúmeros sistemas CAD eletromagnéticos, alguns
deles comercialmente disponíveis e estes sistemas podem diferir signicativamente em suas estruturas e capacidades.
Sistemas CAD modernos incorporam no pré e pós-processadores,
ambas as operações de interaçãocom o usuário e lote (gerenciamento
de informações obtidas). A solução pode ser considerada como a parte
principal do sistema, mas a sua operação normalmente não requer interação do usuário. Por outro lado, a modelagem do problema normalmente envolve uma série de questões relacionadas com a geometria dos
dispositivos em questão e as características esperadas de seus domínios.
2.6 CONSIDERAÇÕES FINAIS DO CAPÍTULO
Neste capítulo, foram apresentadas as bases teóricas do método
dos elementos nitos.
Esse método numérico será utilizado para as
simulações realizadas ao longo de todo o trabalho. No próximo capítulo,
será apresentado um estudo de caracterização de um transformador
monofásico.
60
61
3 CARACTERIZAÇÃO DE UM
TRANSFORMADOR
MONOFÁSICO
Este capítulo apresenta uma técnica sistemática para obtenção
de parâmetros de um transformador monofásico, através da caracterização do material ferromagnético. Essa caracterização é realizada com
o auxílio do ciclo de histerese do material.
Assim, ao longo do capítulo serão explorados, em ordem, os seguintes itens:
ˆ
estudo das principais estruturas de materiais ferromagnéticos;
ˆ
desenvolvimento de um modelo de perdas dos materiais ferromagnéticos;
ˆ
apresentação do dispositivo em estudo;
ˆ
métodos de aquisição do laço de histerese e obtenção do mesmo;
ˆ
apresentação de curvas dos parâmetros elétricos do transformador
em estudo;
ˆ
análises de energia, potência e perdas do modelo desenvolvido;
ˆ
validação do modelo, com a determinação da corrente de
in-rush.
3.1 PERDAS EM MATERIAIS FERROMAGNÉTICOS
A avaliação das perdas nos materiais ferromagnéticos usados na
construção de dispositivos eletromecânicos é um assunto complexo e
multidisciplinar que envolve Física, Engenharia de Materiais e Engenharia Elétrica. A teoria de separação de perdas permite analisar separadamente os diferentes fenômenos físicos que provocam dissipação
de calor em núcleos de estruturas ferromagnéticas (BERTOTTI, 1988).
De acordo com essa teoria, as perdas em materiais ferromagnéticos
submetidos a variações de uxo magnético na operação em corrente
62
alternada podem ser separadas em três componentes: (i) as perdas por
histerese, por ciclo, consideradas constantes para uma dada frequência,
são determinadas experimentalmente utilizando uma fonte de alimentação que opera em uma frequência muito baixa, da ordem de 1 hertz.
Trata-se das perdas por histerese estática ou quase estática, e são causadas pelo deslocamento e rotação dos domínios magnéticos de uma
estrutura submetida à ação de um campo magnetizante externo; (ii)
as perdas causadas pelas correntes parasitas, presentes em meios materiais que apresentam condutividade elétrica elevada; (iii) as perdas
anômalas, também associadas ao movimento dos domínios magnéticos
e explicadas por Bertotti a partir de uma entidade física conhecida
como objeto magnético (BERTOTTI, 1988). Essas perdas podem ser
explicadas, de forma simplicada, como sendo o que resta após as perdas por histerese e por correntes parasitas terem sido subtraídas das
perdas totais.
Em materiais ferrocristalinos, as perdas anômalas são
responsáveis por 50% das perdas totais.
As medições de grandezas magnéticas incluem ensaios em corrente contínua (CC) e em corrente alternada (CA). Os ensaios CC são
voltados para medição de intensidade de campo, uxo magnético, permeabilidade magnética, curvas
BH
e laços de histerese. Já as medições
CA são voltadas principalmente para a medição das perdas nos materiais magnéticos sob condições de magnetização alternada.
A determinação das perdas em materiais ferromagnéticos em unidades de watt/quilograma (W/kg) usualmente parte de condições préestabelecidas: indução magnética máxima de 1,0 T ou 1,5 T e frequência de 50 Hz ou 60 Hz.
Amplamente empregados na construção de
máquinas e transformadores, os materiais ferrocristalinos podem ser
agrupados em três grandes famílias: (i) aços elétricos de grãos orientados (GO) e aços elétricos de grãos não orientados (GNO); (ii) ligas de
ferro-níquel (FeNi) e ferro-cobalto (FeCo); (iii) ferrites de manganêszinco (MnZn) e níquel-zinco (NiZn). Valores típicos das perdas dos materiais ferrocristalinos, ao lado de propriedades eletromagnéticas como
densidade de saturação (BS ), resistividade elétrica (ρ) e máxima permeabilidade magnética relativa (µmax ) são apresentados na Tabela 3.1.
3.1.1 Aços de baixo carbono
Os primeiros transformadores construídos por volta dos anos 80
do século XIX usavam aços de baixo carbono, isto é, com teores inferiores a 0,03% C (CULLITY; GRAHAM, 2009). Estes aços são basica-
63
Tabela 3.1 Materiais ferrocristalinos: propriedades eletromagnéticas.
Categoria
Bs [T]
ρ
µmax [µΩ/m]
Perdas
cas
Aço baixo C
2,1
0,40
Aço GNO
2,0
Aço GO (M-4)
2,0
Aços Ni-B
típi-
[W/kg]*
5000
2,0 (60/1,0)
0,35
8000
2,7 (60/1,0)
0,48
40000
0,9 (60/1,5)
2,0
0,45
-
1,2 (60/1,7)
Fe-(40-50Ni)
1,6
0,48
150,000
110 (50k/0,2)
Fe-(77-80Ni)
1,1
0,55
150,000
40 (50k/0,2)
Fe-(79Ni-4Mo)
0,8
0,58
106
33 (50k/0,2)
Fe-(49Co-2V)
2,3
0,35
50,000
2,2 (60/2,0)
2 · 106
6,000
35 (50k/0,2)
Ferrites (NiZn)
0,35
101 0
4,000
*Os valores entre parentêses indicam a relação f /Bmax [Hz/T]
Ferrites (MnZn)
0,5
mente ferro comercial com algumas impurezas indesejadas de carbono,
normalmente sob a forma de cementita (Fe3 C). Atualmente não são
utilizados na construção de dispositivos elétricos de potência, embora
continuem a ser usados para a construção de pequenos motores onde
as perdas do ferro não são um fator determinante, mas sim o baixo
custo. Como exemplos podem citar-se os transformadores de potência
de reguladores e fonte de tensão, feitos na China.
Em 1900, o metalurgista inglês Sir Robert Hadeld, descobriu
que a adição de silício ao ferro, em pequenas quantidades (inferiores a
3%), diminuía as perdas magnéticas para cerca de 1/4 dos valores nos
aços de baixo carbono (MOSES, 1990). A aplicação deste tipo de aços
começou nos EUA em 1903 e no Reino Unido em 1906. Otimizando-se
o tamanho de grão, através da adição de silício, conseguiu-se que as
perdas magnéticas a 1,5 T e 50 Hz passassem de 7 W/kg nos primeiros
aços para 2 W/kg nos de melhor qualidade hoje em dia. A adição de
silício ao ferro tem as seguintes vantagens:
ˆ
Aumento da resistividade elétrica do material provocando uma
diminuição das correntes de Foucault e consequentemente das
perdas magnéticas;
ˆ
Diminuição da anisotropia magnetocristalina, o que permite um
aumento na permeabilidade magnética;
ˆ
Diminuição da magnetostricção.
A adição do silício ao ferro também apresenta desvantagens, tais como:
64
ˆ
A adição de Si diminui a indução magnética de saturação, em
cerca de 0,05T/%Si (LANDGRAF, 2002),
ˆ
O material se torna mais frágil dicultando o processo de estampagem. Por isso, normalmente as adições de silício estão limitadas
a 3%.
3.1.2 Aços de grão orientado
Os aços de grão orientado (GO) foram descobertos em 1933,
pelo metalurgista americano Norman P. Goss (CULLITY; GRAHAM,
2009). Ele descobriu que se os aços silício fossem laminados a frio com
recozimentos intermédios, a uma temperatura que pode variar entre
◦
900 e 1100 C (MOSES, 1990), e acabando o processo com um reco-
◦
zimento a cerca de 1200 C (liberação de tensões), se conseguia obter
chapas com propriedades magnéticas muito superiores às obtidas por
laminação a quente (CULLITY; GRAHAM, 2009). Este melhoramento
devia-se ao fato de existir uma recristalização secundária que ocorria
durante o recozimento a alta temperatura e que conduzia à obtenção
de uma textura magneticamente favorável, que passou a ser conhecida
por textura de Goss. Nesta textura uma das direções preferenciais de
magnetização de cada grão, a direção [001], está paralela à direção de
laminação e paralela ao plano da chapa, conseguindo-se obter excelentes
propriedades magnéticas segundo a direção de alinhamento do grão.
Nas Figuras 3.1 e 3.2 podem se observar micrograas de aços de
GO e GNO, respectivamente.
3.1.3 Materiais ferromagnéticos amorfos (vidros metálicos)
As ligas metálicas possuem normalmente estruturas atômicas
cristalinas em que os átomos estão ordenados numa rede ordenada e
repetida.
Por outro lado, as ligas metálicas amorfas diferem das an-
teriores pelo fato dos seus átomos estarem distribuídos de um modo
praticamente aleatório e desprovidos de ordem a longa distância (como
nos vidros).
Essas ligas foram descritas pela fórmula geral M70−90 Y10−30 Z0,1−15 ,
onde M é um ou mais metais de transição como o Fe, Ni, Co e Cr, Y é
um elemento não metálico (por exemplo, P, B ou C) e Z é um metalóide
(como o Si, Al ou Ge) (DECRISTOFARO, 1998; VIEIRA et al., 2000).
As ligas magnéticas amorfas utilizadas comercialmente são:
65
Figura 3.1 Grão orientado (GO).
Fonte: adaptado de (GONÇALVES-MONTEIRO, 2010)
ˆ
Fe82 B12 Si6 descoberta em 1978 (METGLAS 2605S),
ˆ
Fe81,5 B13 Si3,5 C2 descoberta em 1979 (METGLAS 2605SC),
ˆ
Fe78 B13 Si9 descoberta em 1980 (METGLAS 2605S-2).
A liga METGLAS 2605S-2 é, atualmente, a mais usada em projetos de sistemas de potência (FISH, 1990; VIEIRA et al., 2000).
Algumas características de materiais ferromagnéticos usados em
núcleos de transformadores estão apresentadas na Tabela 3.2
Para abordar o tema da caracterização dos materiais magnéticos
e sua aplicação na avaliação das perdas é necessário fazer uma abordagem da teoria magnética, explorando o conceito de domínio magnético,
as curvas de magnetização e as perdas magnéticas no ciclo de histerese.
66
Figura 3.2 Grão não-orientado (GNO).
Fonte: adaptado de (GONÇALVES-MONTEIRO, 2010)
3.1.4 Momento magnético, magnetização e materiais magnéticos
Os materiais que sob a ação de um campo magnético produzem
eles próprios, no seu volume e no espaço que os envolve, um campo de
indução magnética Bmag são chamados materiais magnéticos, dizendose que exibem a capacidade de se magnetizar ou se polarizar magneticamente (ROBERT, 1989).
Na escala microscópica, o magnetismo
resulta do movimento de spin dos elétrons no movimento orbital destes
em torno do núcleo. Estes movimentos dão origem ao momentum angular de Spin ou Magnéton de Bohr (mB ), que, na órbita fundamental
do átomo de hidrogênio, vale:
mB =
qe hp
π = 9, 27 · 10−24 [Am2 ]
2me 2
67
Tabela 3.2 Algumas características de materiais ferromagnéticos usados em núcleos de transformadores.
Material
Bsat [T]
Hc [A/m]
ρ [µΩm]
Pmag [W/kg]
e [mm]
MG* 2605 SA1
1,56
2,0
1,3
0,070
0,025
MG* 2605 HB1
1,64
1,5
1,3
0,063
0,025
Aço GO
2,03
4,5
0,5
0,440
0,23
*Material produzido pela empresa METGLAS.
onde
qe
é a carga do elétron,
me
é a massa do elétron em repouso,
é a constante de Plank. O valor de
mB
hp
pode ser positivo ou negativo
de acordo com o spin.
Os dipolos magnéticos estão representados na Figura 3.3.
Figura 3.3 O dipolo magnético tem origem no momento angular dos
elétrons nos íons ou átomos que formam a matéria.
Fonte: produção do autor
A condição de ser gerado um momento magnético não nulo se
deve à existência de subníveis internos incompletos que geram momentos magnéticos que não são anulados pelo elétron com spin contrário.
3s
2
2
2
6
No caso da distribuição eletrônica do Ferro tem-se: 1s 2s 2p
6
2
6
3p 4s 3d . A Figura 3.4 mostra a condição de orbitais e spins a
partir da distribuição eletrônica de Linus Pauling do ferro.
Os 4 elétrons desemparelhados do último subnível do átomo de
ferro dão a ele um momento de dipolo magnético de 4 magnétons de
Bohr. No caso do ferro, no subnível 3d, no primeiro orbital, o momento
é nulo, já nos outros quatro, cada orbital aporta com um momentum,
resultando assim num momento magnético de 4 magnétons de Bohr,
isto é, um material com características ferromagnéticas.
Nos materiais ferromagnéticos, alinhamentos cooperativos de momentos de spin ocorrem em volumes grandes (em relação ao volume
atômico). A magnetização de um material é denida como o momento
68
Figura 3.4 Através do diagrama de Linus Pauling, obtém-se a distribuição dos elétrons nos orbitais. No caso do ferro são 4 momentos
angulares de spin não nulos, isto é, 4 magnétons de Bohr.
(a) Distribuição de Pauling.
(b) Spins nos Orbitais
Fonte: Produção do Autor.
magnético dos dipolos por unidade de volume. Esta magnetização dá
origem aos domínios magnéticos.
3.1.5 Domínios magnéticos (ou, de Weiss): uma questão energética
Vários "spins"de elétrons orientados em uma mesma direção no
cristal de ferro formam o que se chama de domínio magnético.
Este
termo foi cunhado por Weiss em 1906, ainda como sendo uma hipótese na qual a magnetização espontânea é igual à magnetização de
saturação do domínio e seus limites denidos por um campo molecular. Somente em 1949 apareceu a evidência experimental do conceito
de domínio magnético, demonstrado por Williams, Borzort e Shockley
(WILLIAMS; BORZORTH; SHOCKLEY, 1949).
69
Os materiais ferromagnéticos são constituídos por estes domínios
formando regiões volumétricas microscópicas onde os momentos de dipolo magnético se encontram alinhados, procurando a minimização da
energia, com as regiões vizinhas.
A magnitude do campo de magnetização
M
para um sólido como
um todo é a soma vetorial das magnetizações de todos os domínios,
onde a contribuição de cada domínio é ponderada de acordo com a
sua fração volumétrica. No caso de uma amostra não magnetizada, a
soma vetorial apropriadamente ponderada das magnetizações de todos
os domínios é igual a zero.
A Figura 3.5 apresenta uma imagem de metalograa evidenciando os domínios magnéticos.
3.1.5.1 Paredes de domínio
Cada domínio está separado do adjacente por uma zona de transição (interface). Estas zonas chamam-se paredes de domínio ou paredes de Bloch, em homenagem a Felix Bloch que, em 1932, elaborou a
primeira explicação teórica para a estrutura das paredes (CULLITY;
GRAHAM, 2009). A Figura 3.6 representa esquematicamente a estru-
◦
tura de uma parede de domínio de 180 , isto é, uma parede que separa
dois domínios cuja magnetização tem igual direção, mas sentidos opostos.
A Figura 3.7 apresenta uma metalograa de um transformador
fabricado com aço 1010, na China.
As propriedades ferromagnéticas com interesse do ponto de vista
do projeto de máquinas, tais como a histerese magnética (estática e
dinâmica), a permeabilidade, etc., dependem fortemente da estrutura
dos domínios e da forma como estes respondem sob a ação de um campo
magnético aplicado.
A estrutura dos domínios se ajusta de tal forma que tende a
minimizar a energia interna do sistema (da amostra), a qual é composta
pela soma de quatro termos distintos:
ˆ
Energia de anisotropia magnetocristalina,
ˆ
Energia magnetostática,
ˆ
Energia de troca,
ˆ
Energia de magnetostricção, ou magnetoelástica,
Ean ;
Ems ;
Et ;
Emt .
A Figura 3.8 auxilia na compreensão desse fenômeno. Sua descrição no contexto molecular se encontra no Anexo A.
70
Figura 3.5 O tamanho dos domínios está na escala micrométrica e,
para um material policristalino, cada grão pode conter mais de um domínio.
Fonte:produção do autor, obtida através do ensaio de materiais no
CCT, na UDESC.
3.1.6 Magnetização e susceptância magnética
Quando um material magnético é submetido a um campo externo, a indução magnética é dada pela soma dos efeitos devidos ao
campo externo e ao vetor chamado polarização magnética, isto é:
B = µ0 (H + M ).
(3.1)
71
Figura 3.6 Ilustração da parede do domínio magnético que separa
◦
dois domínios cujos momentos atômicos mudam a orientação em 180 .
Fonte: adaptado de (GONÇALVES-MONTEIRO, 2010)
Em módulo, a Equação (3.1) pode ser colocada sob a forma:
M
B = µ0 1 +
H.
H
(3.2)
O termo entre parênteses representa a permeabilidade magnética
relativa do material, portanto:
B = µ0 µr H,
(3.3)
B = µH.
(3.4)
e, nalmente
A Figura 3.9 auxilia na compreensão do fenômeno de magnetização do material magnético.
No caso dos materiais ferromagnéticos o aporte do termo
µ0 H
é
muito pequeno, neste caso, podem se fazer algumas simplicações. A
curva de magnetização do material pode ser aproximada a:
M
M
µr = 1 +
→ µr − 1 =
,
H
H
72
Figura 3.7 Metalograa do núcleo do transformador fabricado na
China aço 1010.
Fonte: produção do autor, obtida através do ensaio de materiais no
CCT, na UDESC.
como
µr 1
(condição de ferromagnetismo),
µr =
M
.
H
(3.5)
A condição de ferromagnetismo ocorre em materiais para os quais
os átomos têm momento magnético permanente relativamente grande.
Além disto, possuem a capacidade de serem magnetizados fortemente
por um campo magnético, mantendo um grau considerável de magnetização quando retirados do campo.
Sobre esta hipótese se obtém a curva do vetor de magnetização
M
H , expresso como M = µr H .
χm de um material é a sua capa-
em função de intensidade de campo
A susceptibilidade magnética
cidade de ampliar o número das linhas de uxo que passam por ele,
denido como:
χm =
M
.
H
(3.6)
73
Figura 3.8 A existência de domínios magnéticos é resultado da minimização de energia.
Fonte: produção do autor.
No caso de ferroressonância, temos que
χm = µr .
Esta capacidade de "ampliar as linhas de força"é utilizada para
classicar o comportamento magnético, neste caso,
Xm > 500 segundo
Xm os ma-
o gráco de permeabilidade relativa, atendendo o valor de
teriais são classicados de acordo com a Tabela 3.3.
Tabela 3.3 Classicação dos materiais quanto à susceptibilidade magnética e a relação de permeabilidade.
Mateial
χm
µ/µ0
Paramagnético
>0
>1
Diamagnético
<0
<1
Ferromagnético
Ferrimagnético
0
0
1
1
Antiferromagnético
>0
>1
A Figura 3.10 apresenta a curva aproximada de magnetização do
transformador estudado nesse trabalho.
3.1.6.1 Curva de magnetização inicial
Um material magnético submetido à ação de um campo magnético crescente
H
vai aumentando a sua magnetização (ou, a sua polari-
zação magnética) até ser atingida a magnetização de saturação, isto é,
74
Figura 3.9 Mecanismo de magnetização não-linear do núcleo.
Fonte: produção do autor
até ser atingida a chamada magnetização técnica. O termo magnetização técnica deve essencialmente pela variação da direção dos domínios
magnéticos saturados e não pela variação da respectiva magnetização
espontânea (CULLITY; GRAHAM, 2009).
Medindo a indução mag-
nética no material (ou, densidade de uxo magnético),
do campo magnético
H
B,
em função
aplicado a uma amostra ferromagnética des-
magnetizada, obtém-se a chamada curva de magnetização inicial ou,
curva de primeira magnetização, onde se observa um comportamento
não linear entre a magnetização do material e o campo externo ao qual
é submetido. Durante a magnetização de um material ferromagnético,
a partir do estado desmagnetizado, podem distinguir-se na curva
BH
várias zonas correspondentes a diferentes etapas do processo de magnetização.
Na Figura 3.11 está apresentada esquematicamente uma
curva de magnetização inicial. A Figura 3.12 apresenta o processo de
magnetização do material sob o enfoque do balanço energético.
75
Figura 3.10 Curva aproximada da magnetização em um material ferromagnético (não linear) obtida pelo produto ponto a ponto
M = Hµr
do gráco permeabilidade versus intensidade de campo.
Fonte: Produção do Autor.
Na zona de deslocamento irreversível das paredes, os domínios
também rodam de forma a alinhar a sua magnetização espontânea com
os eixos cristalográcos preferenciais, cuja direção seja a mais próxima
daquela do campo
H.
Todo este processo de magnetização é irreversí-
vel. Na região, o movimento das paredes não se dá de um modo contínuo, mas sim por variações abruptas conhecidas por saltos de Barkhausen, em homenagem ao físico alemão Heinrich Barkhausen que, em
1919, montou uma experiência em que se ouviam sucessivos estalidos
correspondentes às variações descontínuas na magnetização do material.
Os saltos são gerados pela ancoragem e libertação das paredes
de domínios que se encontram presas (produto de defeitos no material,
impurezas, tensões localizadas, limites de grão). O movimento abrupto
produz uma variação abrupta de uxo magnético, o qual termina induzindo uma corrente na região gerando uma perda conhecida como
perda excedente.
76
Figura 3.11 Curva de magnetização inicial de um material ferromagnético, na região de deslocamento de domínio.
Fonte: produção do autor.
Figura 3.12 Processo de magnetização do material sob o enfoque do
balanço energético.
Fonte: adaptado de (BATISTELA, 2001)
As perdas magnéticas totais que ocorrem num material ferromagnético quando sujeito à ação de um campo de indução
B
variável
no tempo são dadas por:
Pt = Ph + Pf + Pexc
(3.7)
77
onde
Ph
Ph
representa as perdas por histerese,
por correntes de Foucault clássicas e
Pexc
de Foucault excedentes ou, anômalas.
são as chamadas perdas
são as perdas por correntes
Por vezes pode também ser
adotada a divisão em perdas estáticas e dinâmicas em que, as primeiras
correspondem às perdas por histerese, e as segundas às perdas por
correntes de Foucault clássicas e excedentes.
Atualmente existem duas linhas de investigação principais quanto
à interpretação física dos vários mecanismos de perdas. Segundo Bertotti, Cullity e Graham (BERTOTTI, 1988; CULLITY; GRAHAM,
2009; GRAHAM, 1982), entre outros, não existe distinção física entre
os processos de magnetização que ocorrem sob excitação DC ou AC,
isto é, quer em regime quase estático quer em regime variável no tempo,
estes autores consideram que as perdas magnéticas resultam de dissipação de calor por efeito de Joule resultante de correntes de Foucault
induzidas no material. O que difere entre os vários tipos de perdas é
qual o mecanismo interno que as origina. Por outro lado, M. F. Campos
e a equipe de F. Landgraf (CAMPOS; EMURA; LANDGRAF, 2006;
LANDGRAF; EMURA; CAMPOS, 2008), consideram que as perdas
por histerese não têm origem em correntes induzidas no material durante o ciclo de magnetização, mas, sim, na nucleação e aniquilação de
paredes de domínios magnéticos.
3.1.7 Modelos de perdas para materiais magnéticos
A partir das estruturas teóricas que descrevem o comportamento
dos materiais magnéticos, foi possível distinguir três tipos principais
de perdas nesses materiais: perdas por histerese, perdas por correntes
parasitas e perdas excedentes.
3.1.7.1 Perdas por histerese e perdas magnéticas totais
As perdas por histerese,
Ph ,
numa amostra de material ferro-
magnético são proporcionais à área do ciclo de histerese, obtido em
regime quase estático, multiplicada pelo volume da amostra,
frequência de operação
f,
v
e pela
isto é,
I
Ph = f v
HdB
(3.8)
78
Porém, se o mesmo cálculo for efetuado a partir do ciclo de histerese obtido nas frequências industriais de 50 ou 60 hertz, ou superiores,
são adquiridos dados relativos às perdas magnéticas totais da amostra.
Ou seja, em regime dinâmico, a área do ciclo de histerese é uma medida
da energia total dissipada no material por unidade de volume. No m
do século XIX, C.P. Steinmetz obteve uma fórmula empírica que permitia calcular as perdas por histerese em função da indução máxima
no material,
Bm ,
que é,
αh
P h = K h Bm
f
em que
Kh
(3.9)
é a constante de perdas por histerese e que depende das
propriedades do material e
αh
é o chamado coeciente ou expoente de
Steinmetz e que, na equação original de Steinmetz valia aproximadamente 1,6 para os aços.
Atualmente considera-se que
αh
pode variar entre 1,5 e 2 (FISH,
1990) para induções máximas até 1,2 T (LANDGRAF, 2002) e, acima
desse valor até 1,6 T, podem determinar-se experimentalmente valores que podem chegar a
αh = 5
(LANDGRAF; EMURA; CAMPOS,
2008). O aumento do coeciente de Steinmetz acima de determinados
valores de
Bm ,
também foi referido por (BOZORTH, 2000). O meca-
nismo físico que está na origem das perdas por histerese ainda não é
consensual.
Segundo G. Bertotti (BERTOTTI, 1988), C. Graham (GRAHAM,
1982) e Cullity (CULLITY; GRAHAM, 2009), entre outros, as perdas
por histerese têm origem nas micro-correntes de Foucault induzidas no
material, tais como as restantes componentes.
Esta idéia foi inicial-
mente sugerida por Becker (BECKER, 1963), o qual considerou que o
único mecanismo de perdas existente nos materiais magnéticos seriam
as perdas resistivas resultantes de correntes de Foucault.
Em seu conceito fundamental, a origem da histerese encontra-se
no caráter descontínuo do processo de magnetização, na escala submicroscópica. Nesse escopo, a movimentação das paredes de domínios
ocorre de forma discreta, isto é, por saltos quantizados e não através de
um movimento contínuo das paredes. Ou seja, mesmo em uma frequência de operação muito baixa (na ordem de mHz), não há continuidade
no movimento. Logo, os saltos, conhecidos por saltos de Barkhausen,
provocam localmente variação da indução magnética e, portanto, na
força eletromotriz induzida. Essa tensão origina microcorrentes, localizadas em volta dos segmentos em movimento que provocam perdas
por efeito de Joule.
A ocorrência do processo de movimentação por
saltos de Barkhausen resulta da ancoragem das paredes de domínio a
79
impurezas, defeitos cristalinos ou limites de grão, as quais só se libertam quando o campo na vizinhança dessas paredes é suciente para
provocar o seu deslocamento.
3.1.7.2 Histerese através da visão de energia nos domínios
Por outro lado, M. Campos e F. Landgraf et al.
(CAMPOS;
EMURA; LANDGRAF, 2006), consideram que as perdas por histerese
resultam do processo de aniquilação e formação de paredes de domínio
o qual origina dissipação irreversível de energia, independentemente da
existência ou não de correntes de Foucault. As perdas são diretamente
proporcionais à área das paredes nucleadas e aniquiladas durante um
ciclo de magnetização (CAMPOS; EMURA; LANDGRAF, 2006). Segundo estes investigadores uma das provas da teoria que defendem é
o fato do envelhecimento magnético, originado pelas mudanças das estruturas do grão durante o tempo de vida dos aços elétricos, apenas
fazem aumentar as perdas por histerese (CAMPOS; EMURA; LANDGRAF, 2006). Nota-se que o aumento do volume de precipitados no
aço aumenta o número de possíveis pontos de nucleação e aniquilação
de paredes.
Outro aspecto a considerar é o fato da própria estrutura dos
domínios, isto é, o número de paredes em movimento, variar com a
frequência de operação tornando discutível para alguns autores considerar as perdas magnéticas totais como uma soma das perdas em
regime estático e dinâmico (BECKER, 1963).
Parece, pois evidente
que o mecanismo responsável pelas perdas histereses ainda será motivo
de muita investigação.
3.1.7.3 Perdas por correntes de Foucault ou parasitas
Quando uma massa metálica é submetida a uma densidade de
uxo magnético variável, forças eletromotrizes serão induzidas no seu
interior, produzindo correntes que circularão pelo metal. Essas correntes recebem o nome de correntes parasitas (ou correntes de Foucault). A
circulação dessas correntes provoca aquecimento e, consequentemente,
perdas de energia no material ferromagnético.
As perdas por correntes de Foucault clássicas, ou simplesmente
perdas Foucault
Pf ,
resultam da variação temporal do campo de indu-
ção magnética no material o que origina uma corrente induzida e sua
80
grandeza vai depender da resistividade do material. As perdas clássicas por correntes parasitas são calculadas com base nas equações de
Maxwell.
No desenvolvimento do modelo, foi considerado que a condutividade elétrica do material é constante, e isotrópico magnética e eletricamente. Não se leva em consideração o efeito pelicular na distribuição
da corrente só considerando um valor médio da condutividade.
A Figura 3.13 ilustra a lâmina de um transformador.
Figura 3.13 Lâmina de um material ferromagnético.
Fonte: adaptado de (GONÇALVES-MONTEIRO, 2010)
81
Considerando a espessura
e h,
que representa a altura da
lâmina, a partir da lei de Faraday tem-se:
V =
dφ
,
dt
(3.10)
de modo que, a tensao induzida no percurso seja
√
E = 2 2πf Bm hx
(3.11)
e a resistência elétrica do percurso médio lm seja
Rf =
2hρ
.
lm dx
(3.12)
Assim a corrente innitesimal induzida no percurso é
dif =
E
=
Rf
√
2πf Bm lm xdx
.
ρ
(3.13)
A potência de perdas no ferro, por circulação de correntes parasitas, é dada por:
Z
Pf =
0,5e
Z
E dif =
0
0
0,5e
2
2
hlm e3
hlm x2 dx
π 2 f 2 Bm
4π 2 f 2 Bm
→ Pf =
.
ρ
6ρ
(3.14)
Considerando o volume total da lâmina
v = hlm e
(3.15)
tem-se que a perda "Focault"no volume total do ferro é dada por
Pf =
π2 2 2 2
2 2 2 2
B f e v → Pf = kf Bm
f e v .
6ρ m
(3.16)
ρ é a resistividade do material (inuenciada pelo teor de silício),
kf é o coeciente de perdas de Focault, f é a frequência de alimentação,
e é a espessura da chapa e v é o volume total do núcleo.
em que
3.1.7.4 Perdas por correntes de Foucault excedentes
Medindo as perdas magnéticas totais numa lâmina de material
ferromagnético a operar em regime dinâmico, medindo também as res-
82
pectivas perdas por histerese em regime quase estático e calculando as
perdas de Foucault clássicas pela equação (3.16), verica-se que a soma
Ph + Pf
é inferior às perdas totais. A essa diferença chama-se perdas
excedentes ou, anômalas,
Pexc ,
tendo-se então,
Pexc = Pt − (Pf + Ph ).
(3.17)
As perdas excedentes estão associadas com o movimento em larga
escala das paredes de domínios (BERTOTTI, 1988; FIORILLO, 2004)
e respectiva rotação de domínios magnéticos que ocorre na zona dos
joelhos da curva de magnetização.
Segundo o modelo estatístico de Bertotti (com subíndice
B ),
as
perdas excedentes podem ser traduzidas pela equação:
r
Pexc,B = Kexc,B
em que
Kexc,B
1 23 3
Bm f 2
ρ
(3.18)
é um parâmetro relacionado com a estrutura dos domí-
nios magnéticos, sendo diretamente proporcional ao tamanho de grão,
condutividade elétrica
σ,
coeciente de atrito do objeto magnético
seção referente a indução magnética
mv
Vo ,
S,
G,
densidade de massa especíca
e o ente equivalente a um campo coercitivo do objeto magnético
de modo que:
Kexc,B =
8, 76363 p
σGVo S.
mv
(3.19)
Para M. Campos (CAMPOS; EMURA; LANDGRAF, 2006), as
Pexc
(com subíndice
C)
variam de acordo com a equação (3.20), a
constante obtida empiricamente
Pexc,C = Kexc,C
em que o parâmetro
Kexc,C
1 2 3
B f2
ρF e m
(3.20)
é diretamente proporcional à raiz quadrada
do tamanho de grão.
Considerando o modelo de Bertotti pode então escrever-se para
as perdas de ferro totais
Pt =
αh
Kh Bm
f
+ kf e
2
2 2
vBm
f
r
+ KexcB
1 32 3
Bm f 2 .
ρm
(3.21)
83
As perdas por correntes induzidas calculadas de maneira clássica,
o parâmetro mais difícil de ser obtido é a condutividade elétrica do
material devido a não ser homogênea e isotrópica.
3.1.8 Extensão do modelo de perdas sob regime não senoidal
(PWM)
A primeira tentativa da compreensão dos efeitos do conteúdo
harmônico do uxo magnético, como aqueles produzidos pela modulação por largura de pulso (PWM), sobre as perdas em lâminas magnéticas remonta ao ano de 1969 (FISH, 1990).
Hollitscher (HOLLITS-
CHER, 1969) avalia experimentalmente as perdas no ferro com a presença de harmônicos de baixa ordem no uxo, controlando o efeito
desses harmônicos em módulo e em fase. Este estudo concluiu que a
presença de harmônicos acarreta diretamente um forte aumento nas
perdas do ferro.
Através da equação de separação de perdas de Steinmezt-Bertotti
aplicável só a ondas senoidais é possível estender sua aplicação a ondas
não senoidais através da série de Fourier. Para isto, é necessário obter
o espectro da corrente o qual é proporcional ao espectro da indução. A
perda total vai corresponder à soma de todos estes aportes. As Figuras
3.14, 3.15 e 3.16 elucidam esses fatos.
Figura 3.14 Formas de onda estilizadas de tensão PWM e da corrente
que é proporcional à indução. A série de Fourier permite representar
qualquer função como uma soma de ondas senoidais com diferentes
amplitudes e frequências.
Fonte: adaptado de (BATISTELA, 2001)
84
Figura 3.15 A técnica PWM gera uma onda de corrente distorcida que
acompanha a senoide de referência, por efeito da integração da corrente,
com base na constante de tempo
RL
do circuito.
Esse processo de
integração gera exponenciais crescentes e decrescentes que dão o caráter
"recortado"ao sinal de corrente.
Fonte: adaptado de (BATISTELA, 2001)
Embora contrariamente ao esperado o formato de onda PWM
não aumenta em forma expressiva a perda total, no caso da forma
de onda da indução na Figura 3.17 que introduz harmônicas de baixa
frequência (principalmente a terceira e a quinta) gerando laços menores,
as perdas aumentam de forma proporcional ao número de laços.
85
Figura 3.16 Forma da curva
BH
para uma forma de tensão PWM as
ondas recortadas, afetam só o contorno da curva de histerese, seu efeito
sobre as perdas totais é mínimo, num inversor PWM as perdas cam
por conta do aumento da frequência.
Fonte: adaptado de (BATISTELA, 2001)
Figura 3.17 Os dois tipos básicos de forma de distorção da indução
magnética na formação de laços menores na curva de histerese magnética:
(a) sem extremos locais e (b) quatro variações extremas no
período.
Fonte: adaptado de (BATISTELA, 2001)
86
3.1.9 Modelo de Jiles Atherton de histerese magnética e seus
parâmetros ótimos
A curva de histerese corresponde na verdade a energia dissipada
por ciclo, que inclui a histerese propriamente e as perdas por correntes
induzidas ou dinâmicas. Uma modelagem físico-matemática adequada
contribui no projeto de máquinas com melhor eciência energética. Na
procura de representações matemáticas mais elaboradas, o modelo proposto por Jiles-Atherton (JA) (JILES D. C.; ATHERTON, 1983) para
a histerese magnética tem um fundamento físico que provém de uma
série de modelos matemáticos explicando o fenômeno de perdas de ferro
na literatura:
ˆ
Ferromagnetismo de Maxwell, interação mútua entre momentos
magnéticos;
ˆ
Weber, de Weidemann, dipolos magnéticos moleculares;
ˆ
Ewing, interação mútua entre momentos magnéticos;
ˆ
Langevin, teoria matemática do Paramagnetismo;
ˆ
Weiss, interação entre os domínios magnéticos e conceito de indução efetiva magnética no fenômeno ferromagnético.
ˆ
Kersten, Becker e Doring na interpretação da mudança de magnetização do material em termos da movimentação das paredes
dos domínios.
Sua formulação é em termos de uma equação diferencial trans-
cendental de primeira ordem não-linear em função da variável independente de campo magnético
aJA , αJA
e
kJA ).
H,
contendo cinco parâmetros (Ms ,
χs ,
Os valores iniciais são obtidos através de curvas de
histerese experimentais. A otimização dos cinco parâmetros do modelo
−1
JA e Jiles-Atherton inverso (JA
) (JILES D. C.; ATHERTON, 1983)
se baseia em um gráco de magnetização em função da susceptibilidade diferencial
Mr
e
χr ,
e
χin
χm .
Os pontos notáveis:
Ms , Mm , Hm , χm , Hc , χc ,
são denidos a partir das formulações de Jiles (JILES
D. C.; ATHERTON, 1983) e são o ponto de partida para o cálculo
iterativo das variáveis
aJA , αJA
e
kJA
utilizando o algoritmo iterativo
proposto por Peuget (PEUGET, 1995). Na condição de convergência
chega-se aos valores nais para "aJA ,
e Figura 3.19).
αJA
e
kJA "(vericar
Figura 3.18
87
Os parâmetros, iniciais obtidos experimentalmente do gráco de
susceptibilidade, as equações básicas para este m, as denições dos
parâmetros e o algoritmo estão no Anexo B.
Figura 3.18 As susceptibilidades diferenciais são as inclinações das
retas apresentadas na Fig.
O algoritmo de Peuget (PEUGET, 1995)
é aplicado para o encontro de um primeiro possível conjunto de parâmetros. Utiliza-se metade de um laço de histerese para a obtenção dos
nove dados de entrada para o algoritmo.
Fonte: adaptado de (BATISTELA, 2001)
88
Figura 3.19 Pontos chaves sugeridos por Jiles para obtenção dos nove
dados (Ms ,
Mm , Hm , χm , Mr , χr , Hc , χc ,
Hc,
χin )
necessários para a
implementação do modelo JA estão indicados na gura traçada a 1 Hz.
Fonte: adaptado de (BATISTELA, 2001)
3.2 DISPOSITIVO EM ESTUDO
O modelo numérico foi construído seguindo um roteiro proposto
Alfonso Martignoni (MARTIGNONI, 1969) e analisado no software bidimensional FEMM (Finite Element Method Magnetics).
O roteiro
utilizado é apresentado no Anexo C.
Um corte transversal representando o modelo bidimensional pode
ser visto na Figura 3.20.
Ao redor do transformador incluiu-se uma região circular com
ar cuja extremidade é denida com potencial magnético nulo.
Esta
condição de fronteira é denominada contorno de Dirichlet, e tem como
função limitar o domínio de análise.
89
Figura 3.20 Transformador modelado no FEMM.
Fonte: produção do autor.
3.3 MÉTODOS E EQUIPAMENTOS PARA A CARACTERIZAÇÃO DE MATERIAIS FERROMAGNÉTICOS
Nessa seção, o objetivo é apresentar as ferramentas de laboratório que permitem uma adequada caracterização dos materiais (perdas
por kg, curva
BH , permeabilidade, textura GO). A utilização de circui-
tos de baixo custo é uma boa alternativa, já que na maioria dos casos
o projetista precisa fazer comparações qualitativas entre os materiais
que dispõe para o projeto de forma expedita e rápida.
3.3.1 Medidor das perdas de histerese
Este instrumento (vericar Figura 3.21) é utilizado nas empresas de manufatura de núcleos para máquinas elétricas na recepção de
matéria-prima.
Através de uma bobina que produz uma indução especicada
pelo operador e por meio de um circuito eletrônico, calcula-se a energia
90
dissipada no ciclo de histerese no ponto especicado.
O resultado é
apresentado em watt/kg, de modo que é necessário especicar espessura
da chapa.
Figura 3.21 Aparelho de medida DW20.
Fonte: adaptado de (FUKUHARA, 2010).
3.3.2 O quadro de Epstein
A estimativa das características de magnetização dos materiais
e obtenção das perdas magnéticas pode ser realizada através do teste
de Epstein, procedimento padronizado pela norma brasileira NBR-6151
(1996).
O quadro de Epstein assemelha-se a um transformador constituído por dois enrolamentos: primário e secundário (vericar Figuras
3.22 e 3.23). As amostras de teste formam o núcleo magnético do transformador. O quadro de Epstein apresenta ainda um indutor mútuo
para compensar o uxo disperso no interior das bobinas que em consequência da disposição das bobinas é alto. O indutor de compensação
é localizado no centro do espaço formado pelos enrolamentos.
Os enrolamentos apresentam um total de 700 espiras e são recomendados para teste num intervalo de frequência de 25 a 400 Hz.
Excita-se o enrolamento primário e mede-se a tensão secundária.
O
comprimento efetivo para o caminho magnético é adotado convencionalmente como 0,94 m, para o quadro de 25 cm (NBR-6151, 1996). O
material a ser ensaiado deve ser cortado com dimensões especícas.
91
Figura 3.22 Quadro de Epstein - foto.
Fonte: adaptado de (PEREIRA JUNIOR, 2011)
3.3.3 Circuito esquemático
O esquema de ligação para realização do ensaio de perdas magnéticas é ilustrado pelo circuito esquemático representado pela Figura
3.24.
A maioria dos quadros de Epstein existentes no Brasil foram desenvolvidos pela empresa Yokogawa. Essa empresa já não fabrica mais
os medidores de Epstein. Tais medidores podem ser adquiridos junto a
empresas estrangeiras como a Brockhaus, o que diculta e encarece o
ensaio.
3.3.4 O Sensor de lâmina única
O ensaio com o sensor de lâmina única (single-sheet tester) não
é normalizado. O "single-sheet tester"(SST) é composto por dois enrolamentos, que envolvem a tira (vericar Figuras 3.25 e 3.26). O campo
92
Figura 3.23 Quadro de Epstein - ilustração.
Fonte: adaptado de (PEREIRA JUNIOR, 2011)
Figura 3.24 Circuito esquemático para realização do teste de perdas
magnéticas e levantamento da curva
Fonte: NBR-6151, 1996.
BH .
93
magnético externo é aplicado no enrolamento primário, mais externo.
A medição de indução magnética é realizada no enrolamento secundário.
Figura 3.25 Esquema do sensor SST.
Fonte: adaptado de (FUKUHARA, 2010).
3.3.5 Técnica para a medição dos processos de orientação cristalográca (EBSD)
A difração de elétrons retro espalhados (Electron BackScatter
Diraction-EBSD) é uma técnica que fornece informações da orientação
cristalográca obtidas de amostras através da análise de padrões de
difração em um microscópio eletrônico de varredura (MEV).
A análise dos dados obtidos por EBSD é realizada pela observação do mapa (conferir Figura 3.27) de distribuição de orientações
(Orientation Imaging Microscopy-OIM).
Esta técnica é aplicada na avaliação dos processos de laminação
na obtenção de material de grão orientado. A tecnologia de obtenção
e controle do grão tem sido muito explorada devido às vantagens de
eciência energética do equipamento.
A laminação reduz a espessura inicial da chapa e se torna um
indicador do processo.
A técnica de grão orientado melhora a permeabilidade, reduzindo
a área do ciclo de histerese. Com isso, consegue-se melhorar o desem-
94
Figura 3.26 Sensor de lâmina única SST.
Fonte: adaptado de (FUKUHARA, 2010).
Figura 3.27 Exemplo de OIM e código de cores.
Fonte: adaptado de (FUKUHARA, 2010)
95
penho do equipamento em termos de perdas magnéticas, de modo que,
em termos percentuais:
resp =
e
1−
e0
× 100
(3.22)
O circuito proposto também poderia indicar que material apresenta melhor orientação (observar Figuras 3.28 e 3.29).
Figura 3.28 Laminação.
Fonte: adaptado de (FUKUHARA, 2010)
3.3.6 Textura Cristalográca
Os grãos não estão orientados aleatoriamente, privilegiando algumas direções em relação à direção da laminação. A distribuição das
orientações em relação à laminação é conhecida como textura cristalina.
Seu controle permite a fabricação de máquinas de alto rendimento.
As texturas usuais são:
ˆ
Textura Goss. [100]: favorece as propriedades magnéticas, é conhecida como direção espontânea ou de fácil magnetização. Esta
textura é fortemente orientada. Caracteriza o aço silício de grão
orientado, ideal para transformadores e máquinas estáticas;
ˆ
Textura cúbica [101]: índice de magnetização médio, ideal para
motores;
ˆ
Fibra grama [111]: de magnetização difícil. Não apresenta utilidade em qualquer tipo de máquina.
96
Figura 3.29 Magnetização em relação aos índices de Miller de uma
estrutura CCC (Cúbica de Corpo Centrado).
Fonte: adaptado de (FUKUHARA, 2010)
3.4 OBTENÇÃO CURVA DE HISTERESE
O circuito da Fig.
3.30 possibilita investigar o ciclo de histe-
rese de um núcleo magnético. A fundamentação teórica do método de
medição é descrita no Anexo A.
No presente estudo, utiliza-se um núcleo magnético fechado de
um pequeno transformador de teste.
O campo magnético é gerado
pela passagem da corrente na bobina primária ligada ao transformador
variável. O campo
H
é diretamente proporcional à corrente que circula
na bobina primária. Portanto, a queda de tensão
também é proporcional ao campo
H.
VR1
sobre o resistor
Da lei de Ampere,
I
H dl = N1 i1
(3.23)
97
Figura 3.30 Circuito para obtenção da curva de histerese.
Fonte: adaptado de (SILVA, 1995)
Com base na Figura 3.30, a imagem exibida no canal 1 do osciloscópio é proporcional à corrente:
i(t) =
Vch1 (t)
,
R1
(3.24)
N1
Vch1
lm R1
(3.25)
logo:
H(t) =
onde
lm
é o comprimento médio do núcleo,
do primário e
R1
é o resistor
shunt
de
N1
é o número de espiras
1 Ω.
De acordo com a lei de Faraday, a tensão
VS
na bobina secundária
é diretamente proporcional à derivada do uxo total em relação ao
tempo. Empregando-se um circuito
RC
para integrar o sinal
VS
tem-
se, da lei de Faraday:
V2 = N2
escolhendo-se um resistor
R2
dφ(t)
,
dt
(3.26)
apropriado de forma que a maior parte
da queda de tensão ocorra no mesmo:
V2 = ic (t)R2 .
(3.27)
98
No caso, foi escolhido um resistor de
ic (t) = C
100 kΩ,
assim, lembrando-se que
dVc (t)
,
dt
(3.28)
tem-se que
dφ(t)
dVc (t)
=C
R2 .
dt
dt
Vc (t) = Vch2 (t), tem-se que
N2
Como
φ = B(t)S
e
B(t) =
onde
S
R2 C
Vch2
N2 S
(3.30)
N2 é o número de espiras do
C é o capacitor de 1, 5 µF.
H(t) e VC (t) é proporcional a
é a seção transversal do núcleo,
secundário,
R2
No caso,
B(t).
(3.29)
é o resistor de 100
Vr (t)
kΩ
e
é proporcional a
Essas duas tensões são lidas pelos canais 1 e 2 do osciloscópio.
xy (canal 1→eixo x) exibe
B(t) = F (H(t)) do núcleo magnético.
A operação no modo
histerese
a característica de
No caso de se tratar de dispositivos com uma única bobina, como
é o caso de contactores, reatores e até mesmo motores de indução é
possível utilizar uma variação do mesmo circuito, que será apresentado
no Capítulo 4.
Na Figura 3.31, obtêm-se as formas de onda em função do tempo
da tensão e correntes, as quais são proporcionais à indução
intensidade de campo
H(t).
B(t)
e à
Na montagem do circuito ilustrado na
Figura 3.30, foi utilizado um osciloscópio digital TEKTRONICS de 30
MHz.
Na Fig. 3.32 temos o ciclo de histerese do material analisado experimentalmente. Esta curva foi obtida ao multiplicar as 500 amostras
das tensões dos canais do osciloscópio pelos fatores de escala que aparecem nas equações (3.25) e (3.30). Nesse caso, utilizou-se o programa
Excel para produzir os valores de B(t) e H(t).
O cálculo dos fatores de escala baseia-se em dimensões geométricas do equipamento sob análise.
O uso do programa de elementos
nitos auxilia na identicação de valores como: (i) volume de material
magnético
v;
(ii) seção magnética
S;
(iii) comprimento médio de circu-
lação do uxo magnético lm . Assim, ao traçar-se o percurso médio do
uxo no FEMM (conferir Figura 3.33), obtém-se lm
= 0, 168602 [m].
A Tabela 3.4 apresenta um resumo dos dados construtivos do
transformador em estudo.
99
Figura 3.31 Formas de onda dos campos
H(t)
e
B(t),
proporcionais
aos sinais de corrente primária e tensão secundária.
Fonte: Produção do Autor.
Figura 3.32 Curva de histerese do transformador construído utilizando
osciloscópio digital com amostragem de 500 pontos.
Fonte: Produção do Autor.
100
Figura 3.33 Denição do comprimento médio adotado lm
= 0, 1686 m.
Fonte: Produção do Autor.
Tabela 3.4 Resumo dos dados construtivos do transformador.
V1
V2
f
B
S
lm
N1
N2
R1
R2
C
220 V
24 V
60 Hz
10000 gauss
7,6 cm
2
2
(3,9 cm )
0,1686 m
1100 espiras
120 espiras
1R/1W
100kΩ/0,25W
1,5µF/250V
101
Considerando os valores apresentados na Tabela 3.4 e as Equações (3.25) e (3.30), é possível determinar fatores de escala para os
campos
H
e
B , de modo que, fH = 6524, 3 [Ae/V] e fB = 1, 644 [T/V].
3.4.1 Pontos notáveis da curva BH
Considerando a Figura 3.34, é possível determinar os pontos notáveis na curva
BH .
Figura 3.34 O efeito de histerese é gerado pela resistência à movimentação de paredes de domínio.
Fonte: produção do autor
Esses pontos notáveis são:
ˆ
A Remanência (Br ) corresponde ao campo
após a retirada do campo
H
B
(ou seja, quando
residual na amostra
H = 0).
No caso da
curva obtida, a remanência do material magnético foi de 0,75[T].
102
ˆ
A Coercividade (Hc ) corresponde ao campo magnético
sário para reduzir o campo
caso da curva
BH
B
H
neces-
no interior da amostra a zero. No
obtida, foi encontrado um valor de 140[A/m]
para a coercividade. É esse parâmetro que dene o material como
mole ou doce.
ˆ
A Indução de saturação (Bmax ), que corresponde ao ponto de
máxima indução magnética. No caso da curva obtida, seu valor
esteve em torno de 1,5[T].
Na Figura 3.34, o ciclo de histerese é representado pela linha
sólida na cor preta; a curva de magnetização inicial está representada
na cor azul.
A primeira caracterização do material, a partir da curva de histerese, se refere ao campo coercitivo
Hc .
Materiais ferromagnéticos que possuem uma coercividade alta
são denominados duros (coercividade maior que 104 kA/m); aqueles
que possuem coercividade baixa são denominados moles ou doces (coercividade menor que 500 A/m). A Figura 3.35 exemplica o comportamento do laço de histerese para esses casos.
Figura 3.35 Formato do laço de histerese de acordo com o tipo de
material.
Fonte: Produção do Autor.
A Tabela 3.5 apresenta alguns exemplos de cada tipo de material.
Tabela 3.5 Exemplos de materiais duros, moles e intermediários
Materiais duros
Materiais Moles
Materiais intermediários
Ferrites de Ba
Aço Silício
Fe2 O3
Sm-Co
Ferro
CrO2
Ne-Fe-Bo
Mumetal
Tintas metálicas de Fe e Co
103
3.4.2 Obtenção da curva BH
Através de uma interpolação ponto a ponto (valor médio da
soma), implementada com o
ração magnética
BH ,
software
Excel, obteve-se a curva de satu-
que permite a caracterização do material (veri-
car Figura 3.36). Trata-se de um requisito básico no projeto e avaliação
de desempenho de máquinas e equipamentos.
Figura 3.36 Obtenção ponto a ponto da curva de magnetização
BH
a partir da curva de histerese.
Fonte: Produção do Autor.
3.4.3 Identicação do material
A região que caracteriza um material ferromagnético está próxima da região de retentividade da curva de histerese. Ampliando esta
zona é possível identicar dois "candidatos"que mais se aproximam ao
material levantado no laboratório (vericar Figura 3.37). Neste caso se
percebe que o aço carbono 1010 é o mais próximo (vericar Figura 3.38),
na biblioteca do FEMM aparece com uma condutividade de 5,8MS/m e
◦
um ângulo de histerese de 20 . Estes dados são necessários para rodar
a simulação, isto é, a curva
BH
experimental permite identicar o tipo
104
de material e em função de dados de biblioteca se obtém parâmetros
eletromagnéticos (condutividade, ângulo de histerese) e metalúrgicos
(liga aço 1010).
Figura 3.37 Curva de magnetização levantada experimentalmente.
Fonte: Produção do Autor.
3.5 CARACTERIZAÇÃO DO MODELO DE JILES-ATHERTOM
Para traçar a curva de magnetização, a indução
B
da curva de
histerese deve ser multiplicada pelo inverso da permeabilidade do vácuo
µ0 ,
resultando num gráco proporcional ao da curva de histerese.
Os pontos notáveis para a montagem dos parâmetros do modelo Jiles
Athertom, estão indicados na Figura 3.39.
Pontos notáveis da curva denidos a partir das formulações de
Jiles, no Anexo B, são os pontos de partida para o cálculo iterativo das
variáveis
aJA , αJA
e
kJA .
O procedimento de obtenção dos 9 pontos a
partir do gráco de magnetização é claramente ilustrado na curva da
Figura 3.39. Assim,
χin =
∆Min
[−5 − (−5, 329)] · 105
=
= 632.
∆Hin
−173 − (−225)
105
Figura 3.38 Curva
BH
de aço carbono 1010. Nessa nomenclatura, o
número 1000 corresponde família de aços de baixo carbono, enquanto
o número 10 corresponde ao teor de 0,1% de carbono.
Fonte: Produção do Autor através de dados da biblioteca de materiais
do
software
FEMM
Com isso,
Mr = 2, 8 · 105 [A/m],
∆Mr
[−2, 15 − (−3, 416)] · 105
=
= 2694,
∆Hr
23, 5 − (−23, 5)
Hc = 40 [A/m],
χr =
∆Mc
[−9, 49 − (−8, 56)] · 105
=
= 90566,
∆Hc
56, 24 − 36, 31
= 4, 5 · 105 [A/m],
χc =
Mm
Hm = 175 [A/m],
(4, 83 − 3, 99) · 105
∆Mc
=
= 90566,
∆Hc
197 − 250
Ms = 2Mm = 9, 0 · 105 [A/m].
χm =
106
Figura 3.39 Curva de magnetização em relação à intensidade de
campo, obtida a partir da curva de histerese levantada pelo circuito
proposto.
Fonte: produção do autor.
3.6 CURVAS DE GRANDEZAS MAGNÉTICAS DO TRANSFORMADOR
Nesta seção, são apresentadas as curvas da variação das grandezas magnéticas do transformador, como permeabilidade, indutância e
relutância, em função das características do material que o constitui.
3.6.1 Curva da permeabilidade magnética diferencial
Através da curva
BH
obtida ponto a ponto é possível calcular
sua derivada nos pontos em questão, com o auxílio de programas feitos
em MatLab ou Excel, para se obter a curva de permeabilidade absoluta
diferencial.
107
Com a curva de permeabilidade absoluta do material em função da intensidade de campo, podem ser obtidas outras curvas como:
permeabilidade relativa, indutâncias primária e secundária, indutância mútua, magnetização, susceptibilidade, relutância e permeância.
Assim, com essa informação, é possível ter uma visão qualitativa da
operação da máquina para diferentes correntes de operação, ajudando
a denir melhor os critérios de projeto adotados.
É importante destacar que existem vários tipos de permeabilidades magnéticas para um dado material (BERTOTTI, 1988; BOZORTH,
2000). São eles:
ˆ
Permeabilidade normal, ou simplesmente permeabilidade
dada pela razão
B/H
µ,
é
obtida a partir do material no estado des-
magnetizado;
ˆ
Permeabilidade inicial,
BH
ˆ
µi ,
obtida a partir do declive da curva
na origem;
Permeabilidade máxima,
µmax ,
que é o maior valor obtido para
a permeabilidade normal;
ˆ
Permeabilidade diferencial,
dB/dH
µdif ,
que é calculada pelo declive
para um dado ponto da curva de magnetização.
A Figura 3.40 apresenta a curva da variação da permeabilidade
relativa do material magnético em estudo.
Observa-se que usualmente se utiliza uma densidade magnética
de 1,0 [T] no projeto de transformadores.
Assim, com a curva
BH
caracterizada pode-se estimar, com um erro pequeno, a corrente de
excitação de uma máquina e com isto as perdas a vazio.
108
Figura 3.40 Permeabilidade magnética relativa em função da intensidade de campo. Teoricamente, esta curva deveria partir do zero.
Fonte: Produção do Autor.
3.6.2 Permeabilidade magnética do núcleo em função da corrente primária
A partir do gráco da permeabilidade magnética em função da
intensidade de campo, é possível plotar a relação da permeabilidade
versus corrente. Esse gráco permite visualizar como a relação das correntes de operação está atrelada à permeabilidade magnética do material.
A permeabilidade relativa se obtém através da relação
µr =
µabs
µ0
e a corrente através da lei de Ampere, de modo que:
i1 =
lm
0, 1686
H(t) =
H(t).
N1
1100
(3.31)
A Figura 3.41 exprime a permeabilidade em função da corrente
de excitação primária.
109
Figura 3.41 Permeabilidade magnética relativa em função da corrente
de excitação primária.
Fonte: Produção do Autor.
3.6.3 Indutâncias próprias L1 e L2 em função da corrente primária
Da lei da Faraday e de Ampere se obtém uma expressão para as
indutâncias presentes no transformador, de modo que:
dφ
,
dt
N1 i1
H=
,
lm
B = µH,
V1 = N1
φ = BS.
(3.32)
(3.33)
(3.34)
(3.35)
Relacionando (3.32), (3.33), (3.34) e (3.35), temos que:
φ=
e
V1 =
N1 S
µ(i)i(t)
lm
N12 S
di(t)
µ(i)
.
lm
dt
(3.36)
(3.37)
110
Da denição de indutância
Nφ
,
i
(3.38)
N12 S
µ(i) [H].
lm
(3.39)
L=
temos que a indutância primária é:
L=
Isto é, a indutância primária é proporcional à permeabilidade
magnética que, por sua vez, depende da corrente de excitação.
Como
S , N1
e lm
1 são constantes, podemos reescrever a Equação
(3.39) de modo que:
L1 = KL1 µr (i),
com
KL1 =
SN12 µ0
= 0, 006855.
lm
(3.40)
(3.41)
Observar que a Equação (3.40) está em termos da permeabilidade
relativa.
De forma análoga a indutância própria do secundário pode ser
obtida:
com
KL2 =
L2 = KL2 µr (i),
(3.42)
SN22 µ0
= 0, 00008153.
lm
(3.43)
Da relação, entre as indutâncias se chega a uma expressão que
relaciona o número de espiras e a relação de transformação, que será
utilizada para simplicar cálculos nas seções seguintes:
L1
N1
=
= a2
L2
N2
(3.44)
1 O parâmetro l , na realiadade, varia com a saturação magnética do material.
m
Contudo, para efeitos de simplicação, considerou-se que o comprimento médio
geométrico é igual ao comprimento médio magnético do material.
111
3.6.4 Obtenção experimental da indutância primária e secundária
Através dos fatores de proporcionalidade obtidos anteriormente
se torna simples traçar as curvas de indutância primária e secundária
a partir da curva de permeabilidade.
A curva da indutância (conferir Figuras 3.42, 3.43 e 3.44) são
obtidas derivando a curva de magnetização através de programas como
Excel ou MatLab.
Figura 3.42 A curva da indutância primária é obtida multiplicando as
ordenadas da característica permeabilidade versus corrente pelo fator
KL1 .
Fonte: Produção do Autor.
112
Figura 3.43 Utilizando programa de elementos nitos, a indutância
foi calculada considerando uma corrente de magnetização de 50 [mA].
Mas, existe um erro nesse valor porque a corrente de vazio é a soma da
corrente de magnetização de 47mA e uma outra corrente, associada as
perdas do ferro, considerando resistor equivalente
Rn = 12665 [Ω], cujo
valor é 17 [mA]. Assim, refazendo as contas com 47 [mA], se obtém a
curva corrigida, sendo essa muito próxima da curva experimental.
Fonte: Produção do Autor.
Figura 3.44 Indutância própria secundária, obtida através do fator de
proporcionalidade
KL2 .
Fonte: Produção do Autor.
113
3.6.5 Cálculo de indutâncias mútuas
A partir da Lei de Faraday, tem-se que
dφ di1
di1 dt
(3.45)
S
di1
µ(i)
.
lm
dt
(3.46)
V1 = N1
que pode ser reescrita como
V1 = N12
Analogamente, para o secundário, tem-se que:
V2 = N2
dφ di1
di1 dt
(3.47)
que pode ser reescrita como
di1
S
V2 = N2 N1 µ(i)
.
lm
dt
(3.48)
Assim, pode-se inferir que a tensão induzida no bobinado secundário, em função da corrente de excitação primária, é dado por:
V12 = M12
di1
,
dt
(3.49)
com o fator que relaciona a tensão com a derivada temporal da corrente,
denominado indutânica mútua, dado por:
M12 = N1 N2
S
µ(i) [H].
lm
(3.50)
Analogamente, a tensão induzida no bobinado primário, em função da corrente de excitação secundária, é dado por:
V21 = M21
com:
M21 = N2 N1
di2
,
dt
S
µ(i) [H],
lm
(3.51)
(3.52)
114
de modo que
M21 = M12 = LM = N1 N2
S
µ(i),
lm
(3.53)
cuja estrutura é similar à observada nas indutâncias próprias:
S
µ(i),
lm
S
L2 = N22 µ(i).
lm
L1 = N12
O quociente
S/lm
(3.54)
(3.55)
nas equações (3.53), (3.54) e (3.55) é o mesmo.
Isso permite relacionar os três valores de indutâncias como:
L2
LM
L1
= 2 =
.
N12
N2
N1 N2
(3.56)
A relação de transformação é denida como
a = N1 /N2 .
Uti-
lizando essa relação de transformação, a indutância mútua pode ser
expressa em função da indutância própria primária ou secundária:
e
L1
LM
L1
=
→ LM =
N12
N1 N2
a
(3.57)
L2
LM
=
→ M = aL2 .
N22
N1 N2
(3.58)
Isto é, a indutância mútua pode ser calculada em função da indutância primária ou secundária desde que a relação de transformação
seja conhecida.
A partir disso, foi gerada a curva que expressa a in-
dutância mútua em função da corrente de excitação do transformador
(Figura 3.45).
O valor experimental obtido para a indutância mútua foi de
1,15[H]. Contudo, este valor se altera em função da corrente de magnetização.
3.6.6 Curva de Relutância
Análoga a resistência, a relutância expressa a diculdade à pas-
lm
µ(i)S , onde lm
a seção transversal do
sagem de linhas de força, denida pela relação:
corresponde ao percurso médio do uxo e
S
< =
115
Figura 3.45 Indutância mútua vista do secundário por efeito da corrente primária.
Fonte: Produção do Autor.
núcleo,
lm = 0, 1686[m]
e
S = 0, 76 [cm2 ].
A curva experimental da
relutância é apresentada na Figura 3.46.
3.6.7 Curva da permeância
A Permeância
pm
se dene como o inverso da Relutância (1/<),
é propriedade que facilita a passagem de uxo pelo circuito magnético,
equivale à condutância no circuito elétrico:
pm = µ(i)
S
[Wb/A]
lm
(3.59)
em que facilmente se percebe que é proporcional à permeabilidade absoluta. A curva experimental da permeância é apresentada na Figura
3.47.
116
Figura 3.46 Curva da relutância em função da corrente primária.
Fonte: Produção do Autor.
3.6.8 Considerações sobre a permeabilidade e a curva BH
A partir da curva
BH ,
determina-se a permeabilidade do mate-
rial. A derivada da permeabilidade em relação à corrente é proporcional
a indutância primária e secundária, dependendo dos dados geométricos
e o número de espiras do circuito.
As derivadas da permeabilidade em relação as correntes vistas
do lado primário e secundário são iguais.
Através das curvas levantadas e da geometria do dispositivo é
possível realizar qualquer cálculo eletromagnético em forma gráca com
uma precisão na maioria dos casos em torno dos 5%.
3.7 CÁLCULO DE INDUTÂNCIAS EM UM PONTO DE
OPERAÇÃO
Esta seção apresenta o cálculo das indutâncias do transformador,
em ponto de operação, através de diversos métodos.
117
Figura 3.47 Curva da permeância do circuito primário em função da
corrente de magnetização no enrolamento primário.
Fonte: Produção do Autor.
3.7.1 Cálculo das indutâncias mútuas e reatância de dispersão
pelo método concatenado
Para realizar esse cálculo, é necessário considerar a inuência da
corrente de magnetização. A Figura 3.48 auxilia a compreender a distribuição de correntes no primário de um transformador real. Observar
que essas correntes possuem um aspecto fasorial.
É fácil perceber que
R=
Ir
pode ser determinada com:
2202
220
V2
=
= 13, 4 kΩ → Ir =
= 16, 4 mA.
P
3, 6
13400
A corrente de magnetização pode ser obtida a partir da Lei de
Im = 33, 16 [mA]. Desse modo, tem-se que
I0 = IR + jIm = 16, 4 + 33, 16 [mA]. Para a simulação no FEMM, é
necessário utilizar a corrente de pico, assim: I0 = 23, 19 + 46, 9 [mA],
observar que |I0 | = 52, 0 [mA].
O módulo da corrente de entrada no primário I1 é 100 [mA].
0
Contudo, essa corrente corresponde à soma I1 = I1 + I0 . Assim, I1 =
Amperé, de modo que,
118
Figura 3.48 Distribuição de correntes em um transformador real.
Fonte: produção do autor.
88, 19 + j46, 9. Com
aI10 = 596 [mA].
isso,
I10 = I1 − I0 = 65
[mA]. Tem-se que
I2 =
Utilizando-se esses valores na simulação do FEMM, tem-se que
L1 = 8, 6535
[H],
L2 = 0, 1581
M12 =
[H]
λ12 = 0, 092
[Wb]. Tem-se que:
λ12
= 0, 9422 [H].
i1
Sabe-se que
M21 = a2 M12 = 8, 6399 [H].
A indutâcia de dispersão do primário l1 é dada por:
l1 = L1 − M12 ∗ a = 13, 5 [mH.]
Por m, a indutância de dispersão do secundário l2 é dada por:
l2 = L2 −
M21
= 0, 066 [mH.]
a
119
3.7.2 Cálculo de indutâncias mútuas por energia em condições
de polaridade aditiva e subtrativa (bucking test )
No transformador os uxos primários e secundários se opõem (lei
de Lenz), isto é,
φ1 −φ2 = φ0 , o uxo magnético resultante corresponde
ao gerado pela corrente de magnetização, levando ao transformador
trabalhar num determinado ponto da curva
BH ,
condição natural de
operação do transformador.
Se o transformador fosse simulado numa condição de uxos primário e secundário em adição, isto nos levaria ao valor máximo de uxo
na curva
BH ,
que corresponde à indução máxima
campo máxima
Bs
e intensidade de
Hs .
Através deste procedimento é possível percorrer toda a curva
BH
e calcular parâmetros como a indutância mútua e a reatância dispersiva.
Assim, considerando a densidade de energia na curva
BH , tem-se
que:
Z
w=
Z
w=
Lembrando que
H dB,
(3.60)
B
1 2
dB, =
B .
µ
2µ
(3.61)
B = µH
e
B=
Hlm = N i,
tem-se que:
µN1 i1
.
lm
(3.62)
Reescrevendo (3.63), tem-se que:
w=
multiplicando pelo volume
1 µ2 N12 2
i1 .,
2
2µ lm
v = Slm ,
W =
(3.63)
tem-se que a energia é dada por:
1 µN12 S 2
i .
2 lm 1
(3.64)
Assim, a energia acumulada na condição de ligação aditiva é
dada por:
Wa =
L1 i21
L2 i22
M i 1 i2
+
+
2
2
2
(3.65)
120
e a energia acumulada na condição de ligação subtrativa é dada por:
Wb =
L1 i21
L2 i22
M i 1 i2
+
−
.
2
2
2
(3.66)
Fazendo (3.65) - (3.66):
LM =
Wa − W b
.
i1 i2
(3.67)
Esta expressão está apresentada supondo valores de corrente do
tipo RMS. O FEMM utiliza valores de corrente de pico, desta forma a
expressão em termos da corrente de pico ca:
LM =
2(Wa − Wb )
.
i1 i2
(3.68)
Dadas as considerações de operação do ensaio anterior, após simular no FEMM tanto na condição acumulativa quando na diferencial,
Wd = 0, 0101992 [J] e Wa = 0, 0617093 [J]. Com isso, utiLm = 0, 8642. Além disso, L1 = 8, 6535 e
L2 = 0, 8642.
Desse modo, a indutância de dispersão do primário l1 é dada
tem-se que
lizando (3.68), obtém-se
por:
l1 = L1 − aLM = 729 [mH],
e a indutância de dispersão do secundário l2 é dada por:
l1 = L1 −
LM
= 63, 8579 [mH].
a
3.7.3 Cálculo das indutâncias pelo método gráco
Considerando as mesmas condições de ensaio dos testes anteriores, pode-se determinar as indutâncias através das curvas traçadas na
Seção 3.6.
Assim, a Figura 3.49 apresenta a curva de indutância primária,
com a indutância no ponto de operação em que se trabalha.
Assim, a Figura 3.50 apresenta a curva de indutância secundária,
com a indutância no ponto de operação em que se trabalha.
Assim, a Figura 3.51 apresenta a curva de indutância mútua,
com a indutância no ponto de operação em que se trabalha.
121
Figura 3.49 Indutância primária de 8,28 [H] no ponto de operação.
Fonte: produção do autor.
Figura 3.50 Indutância secundaria de 0,095 [H] no ponto de operação.
Fonte: produção do autor.
122
Figura 3.51 Curva indutância mútua em função da corrente primaria
na condição sem carga o valor para a indutância gracamente está em
torno de 0,903 [H] para uma corrente de primaria de 100 [mA]
Fonte: produção do autor.
3.7.4 Fator de acoplamento
O fator de acoplamento é denido como:
LM
K=√
,
L1 L2
(3.69)
de modo que seu valor máximo é a unidade.
Dessa forma, para o método dos uxos concatenados, o fator
K = 0, 81.
K = 0, 73.
de acoplamento é
acoplamento é
Para o médoto da energia, o fator de
123
3.8 DETERMINAÇÃO EXPERIMENTAL DAS INDUTÂNCIAS MÚTUAS NO PONTO DE OPERAÇÃO
Para um transformador ideal, como mostrado na Figura 3.52,
podem-se obter as seguintes equações no domínio do tempo:
di1
di2
+M
,
dt
dt
di2
di1
V2 = L2
+M
.
dt
dt
V1 = L1
(3.70)
(3.71)
Figura 3.52 Modelo ideal de transformador monofásico.
Fonte: produção do autor
No domínio da frequência, tem-se:
V1 = jω(L1 I1 + LM I2 ),
(3.72)
V2 = jω(L2 I2 + LM I1 ).
(3.73)
Para a situação indicada na Figura 3.53 observa-se que:
Vx = V1 + V2
(3.74)
ix = i1 = i2 .
(3.75)
Considerando as Equações (3.72) e (3.73), tem-se que:
Vx |Zx | = = ω(L1 + L2 + 2M ).
Ix
(3.76)
124
Figura 3.53 Circuito para cálculo das mútuas.
Fonte: produção do autor
Para a situação indicada na Figura 3.54 observa-se que:
Vx = V1 − V2
(3.77)
ix = i1 = −i2 .
(3.78)
Considerando novamente as Equações (3.72) e (3.73), tem-se que:
Vy |Zy | = = ω(L1 + L2 − 2M ).
Iy
Figura 3.54 Circuito para cálculo das mútuas.
Fonte: produção do autor
(3.79)
125
Utilizando as Equações (3.76) e (3.76) chega-se nalmente a
equação da indutância mútua:
LM =
|Zx | − |Zy |
.
4ω
(3.80)
Aplicam-se as tensões indicadas mantendo a mesma corrente em
ambos ensaios , neste caso de 100mA, obtendo as impedâncias nas
condições de polaridade aditiva e subtrativa , variando a tensão. Assim:
Vx = 319 [V],
Ix = 71 [mArms ],
Vy = 234 [V],
Iy = 71 [mArms ].
Logo,
Vx
319
= 4493 [Ω],
=
Ix
0, 071
Vy
234
= 3296 [Ω],
Zy =
=
Iy
0, 071
Zx =
e, por consequência,
LM =
4493 − 3296
= 0, 794 [H] ≈ 0, 8 [H].
4 · 2π · 60
3.9 MODELAGEM DO TRANSFORMADOR
Para modelar o núcleo do transformador realizou-se o ensaio de
vazio. Para simular a transformador trabalhando na condição de vazio,
primeiramente deve-se determinar a sua corrente de vazio. Para este
m, utiliza-se a curva
BH
obtida experimentalmente para obter os
parâmetros do transformador relacionados a esse ensaio.
3.9.1 Cálculo da corrente de vazio (corrente de magnetização)
φ√
= φm sin(ωt),
Vpk = 220 2 = N φm ω .
Considerando um uxo magnético senoidal
expressão para a tensão de pico é dada por
a
126
A expressão para a densidade magnética máxima, considerando
N = 1100 [e]
e
S = 7, 6 [cm2 ]:
Bm =
Vpk
= 0, 9876 [T],
N Sω
(3.81)
o que se aproxima do valor de 1 [T] do gráco. Ainda da curva
obtém a intensidade de campo
Hlm = N i → i =
H
BH ,
se
e da lei de Ampere:
350 [Ae/m] · 0, 1686 [m]
= 0, 054 [A],
1100 [e]
(3.82)
sendo que o valor RMS da corrente é
0, 054
√ = 0, 038 [Arms ].
2
Como pode-se ver, o valor teórico através da curva
o experimental através de um amperímetro
true
BH
obtido e
RMS é próximo.
Nas simulações é utilizado o valor de 0,052[A] que corresponde
ao valor de corrente experimental de 37 mA rms.
3.9.2 Modelagem do núcleo do transformador
Uma vez localizada as características do material na biblioteca
e com a corrente de magnetização é possível rodar a simulação.
O
programa utiliza um modelo série para o núcleo (observar Figura 3.55),
sendo que habitualmente a literatura apresenta um modelo paralelo.
Em decorrência disso, faz-se uma mudança de associação série para
associação em paralelo através de uma transformação de impedâncias.
3.9.3 Transformação de impedâncias
Uma impedância formada por um resistor e um indutor em série
pode ser representado por um circuito equivalente paralelo, formado
também por um resistor e indutor equivalentes (observar Figura 3.56).
Separando partes real e imaginária:
Rs =
2
Rp Xlp
2
Rp2 + Xlp
(3.83)
127
Figura 3.55 Modelo série do transformador utilizado pelo FEMM.
Fonte: Produção do Autor.
Figura 3.56 Transformação circuito série para circuito paralelo.
Fonte: Produção do Autor.
e
Xs =
Rp2 Xlp
2
Rp2 + Xlp
(3.84)
128
de modo que:
2
Rp2 + Xlp
=
Rp2 Xlp
Rs
(3.85)
2
Rp2 + Xlp
=
2
Rp Xlp
.
Xs
(3.86)
e
Igualando (3.85) com (3.86) obtém-se:
Xlp
Rp
Xs
Rp
=
→
=
.
Rs
Xs
Rs
Xlp
Em (3.83), fatorando-se
(3.87)
2
Xlp
e com as relações em (3.87) se obtém
a resistência paralela equivalente:
Rs =
"
Rp
2
Rp
2
Xlp
→ Rp = Rs
+1
Xs
Rs
#
2
+1 .
(3.88)
Analogamente
"
Xlp = Xs
Rs
Xs
#
2
+1 .
(3.89)
Considerando a corrente de vazio de 52 mA, ao modelar-se o
núcleo no FEMM, obtém-se no primário:
ˆ
Corrente total = 0,052 A;
ˆ
Queda de tensão = 139,613+j 292,947 V;
ˆ
Fluxo concatenado = 0,777066-j 0,368843 Wb;
ˆ
Fluxo/Corrente = 14,9436-j 7,09314 H;
ˆ
Tensão/Corrente = 2684,86+j 5633,6
Ω.
Os valores da simulação para o resistor série
a reatância indutiva série
Rs = 2684Ω
e para
Xs = 5634Ω.
A resistência paralela equivalente é dada por:
"
Rp = Rs
Xs
Rs
2
#
+ 1 = 2684
"
5634
2684
2
#
+ 1 = 14510 Ω.
(3.90)
129
A reatância paralela equivalente é dada por:
"
Xlp = Xs
Rs
Xs
#
2
"
+ 1 = 5634
2684
5634
#
2
+ 1 = 6914Ω.
(3.91)
O modelo série apresentado pelo programa FEMM para uma
determinada corrente de operação, está atrelada a uma tensão, que
neste caso, é de 324 V (229
Vrms
).
No modelo paralelo a tensão
e considerada 220 V, assim para impor a mesma corrente é necessário
compensar a os valores de impedâncias obtidos por um fator de 311/324.
Dessa forma:
Rp =
e
Xlp =
311
14510 = 13927Ω
324
311
6914 = 6636Ω → Lp = 17, 61 [H].
324
3.9.4 Modelo através de ensaios experimentais
Pelo fato de ser um transformador de pequeno porte não foi
possível utilizar wattímetros, por conta do intervalo da escala naqueles
que estavam disponíveis no laboratório.
O problema foi contornado
utilizando osciloscópio e um multímetro true rms, além de ferramentas
da matemática fasorial.
No ensaio de circuito aberto, utilizou-se uma tensão rms de 277 V
e uma corrente true rms de 71 mA. O defasamento observado foi de 62º.
A Figura 3.57 mostra as curvas obtidas nesse ensaio.
Com essa defasagem, é possível obter as correntes sobre o resistor
e o indutor do modelo paralelo. Dessa forma,
IR = I cos(62) = 33, 3 [mA]
e
IL = I sin(62) = 62, 68 [mA].
Com isso,
Rn = 8310Ω
e
L = 11, 72 [H].
Para a condição de curto circuito, utilizou-se tensao de 7,8 V e
a mesma corrente de 71 mA. O defasamento obtido nessa condição foi
de 5º. A Figura 3.58 mostra as curvas obtidas nesse ensaio.
130
Figura 3.57 Forma de onda da corrente de excitação em vazio para
uma corrente de 100mA, torna-se necessário aumentar a tensão para
atingir este valor.
Fonte: produção dos autor.
Figura 3.58 Forma de onda da corrente e tensão no ensaio de curto
circuito.
Fonte: produção dos autor.
131
Nesse ensaio, toma-se o modelo série do transformador (com a
resistência do cobre e a indutância de dispersão). Assim,
VR = I cos(5) = 7, 77 [mA]
e
VL = I sin(5) = 0, 6798 [mA].
Com isso,
R1 = 54, 7Ω, R2 = 0, 72Ω, l1 = 12, 7 [mH]
e
l2 =
0, 151 [mH].
3.10 MODELAGEM DAS PERDAS NO TRANSFORMADOR
Através do modelo matemático apresentado na Figura 3.59, é
possível determinar as perdas no transformador. Considerar:
ˆ R1 :
Resistência equivalente primário;
ˆ x1 :
Reatância de dispersão primaria;
ˆ Z1 :
impedância vista do lado primário;
ˆ R2 :
Resistência equivalente secundário;
ˆ x2 :
Reatância de dispersão secundaria;
ˆ Z2 :
impedância vista do lado secundário;
ˆ Rc :
Perdas do núcleo;
ˆ Xm :
Reatância de magnetização.
Da relação de transformação
a,
pode-se representar as grande-
zas do secundário em um circuito equivalente, visto do lado primário
(Figura 3.60) ou secundário.
Para a condição de transferência máxima de potência a impedância da fonte deve ser igual à da carga, no caso em particular do
circuito apresentado:
Z1 = a2 Z2
(3.92)
R1 = a2 R2
(3.93)
x1 = a2 x2 .
(3.94)
assim,
e
132
Figura 3.59 Modelo circuital do transformador.
Fonte: Produção do Autor.
Figura 3.60 Modelo circuital do transformador reetido ao primário.
Fonte: Produção do Autor.
Associando-se as grandezas, tem-se como parte real
a2 R2
e
xleq1 = x1 + a2 x2 .
Req1 = R1 +
133
3.10.1 Cálculo das resistências primária e secundária do bobinado
Através da simulação se obtêm as perdas no cobre, nas bobinas
primária e secundária. Para as correntes primária de
secundária de
I2 = 3, 3718
A, com
I1 = 0, 4197
A e
a = 9, 17.
Através da simulação no FEMM, a perda na bobina primária é
P1 = 0, 9518 W e na secundária é de P2 = 2, 12 W. Assim, no total,
tem-se que P = 3, 1W. Com esse total, é possível calcular a resistência
de
equivalente, de modo que:
Req1 = 2
3.1
= 46Ω
0.36772
(a multiplicação por dois se deve ao fato de ser a corrente de pico).
Assim,
R1 =
Req1
= 23Ω
2
R2 =
R1
= 0, 27Ω.
a2
e
3.10.2 Obtenção experiemental das perdas resistivas e a dispersão magnética
Pelo fato de não haver disponível miliwattimetros para potências
baixas, utilizou-se a matemática fasorial e o uso de formas de onda
(Figura 3.61) para a análise do ensaio de curto-circuito experimental.
Assim, foi utilizado um procedimento semelhante ao utilizado no ensaio
de circuito aberto.
Do circuito RL série (Figura 3.62), proposto para avaliar as perdas e dispersão magnética, obteve-se:
ˆ I1cc = 0, 253
ˆ Vcc = 28, 1
ˆ
A, corrente primária na condição de curto circuito;
V => Tensão reduzida primária;
Ângulo de desfasamento
≈ 4, 085◦ .
Como se trata de um circuito série a corrente que gera as quedas
de potencial é a mesma, e depois de operações matemáticas obteve-se:
Vr = 28, 1 cos 4, 085 = 27, 93 →= Req1 =
Vr
= 110, 4Ω.
Icc1
134
Figura 3.61 Forma de onda da corrente e tensão no ensaio de curto
circuito.
Fonte: Produção do Autor.
e
Vl = 28, 1 sin 4, 085 = 27, 93 →= Xleq1 =
Vl
= 7, 72Ω.
Icc1
Em função das relações (3.93) e (3.94), tem-se
Xl1 =
e
Xl2 =
Xleq1
= 3, 86Ω → L1 = 10, 24 mH
2
Xleq1
= 0, 046Ω → L2 = 0, 0122 mH.
2a2
R1 =
e
R2 =
Req1
= 55, 2 [Ω]
2
Req1
= 0, 656 [Ω].
2a2
135
Figura 3.62 Modelo série do ensaio de curto circuito no transformador.
Fonte: Produção do Autor.
Estas medições, em função da grande discrepância entre os valores teóricos, foram realizadas 5 vezes obtendo valores similares. Uma
hipótese é que o programa de elementos nitos é bidimensional de tal
forma que o 50% da espira não é considerada.
3.10.3 Perdas no ferro
As perdas foram determinadas através da curva de histerese,
onde sua área multiplicada pelo volume de ferro representa as perdas
sobre o ferro. Estas perdas são identicadas como: Perdas de histerese,
perdas Foucault e anômalas.
Através da caracterização da curva
BH
se obteve da biblioteca
o material mais aproximado à curva experimental, neste caso, corresponde ao material de aço de baixo teor de carbono, aço 1010. Neste
material a condutividade apresentada é de 5,8MS/m e um ângulo de
136
◦
histerese máxima de 20 .
Com estes dados as perdas atingiram 3,6
Watts nas condições nominais onde a corrente primária nominal é de
I1 = 0, 4197
[A] e uma secundária
I2 = 3, 3718
[A].
O valor obtido para as perdas de cobre e ferro caram próximos,
o que faz concluir que os valores utilizados no projeto estão corretos.
3.10.4 Perdas Totais
As perdas totais são dadas pelo somatório das perdas no cobre
bobina primária, das perdas no cobre bobina secundária, das perdas no
ciclo de histerese e das perdas Foucault, logo:
Pt = (Pf + Ph ) + Pcu1 + Pcu2
(3.95)
Pt = 3, 6 + 1, 19565 + 2, 088 = 6, 88 [W].
(3.96)
assim
3.11 ENERGIA DISSIPADA NA CURVA DE HISTERESE
A energia dissipada na curva do ciclo de histerese como consequência do deslocamento dos domínios magnéticos do material acarreta uma perda, no núcleo e corresponde a área da curva de histerese
multiplicada pelo volume de ferro atravessado pelo campo magnético.
A curva de histerese obtida experimentalmente, como ilustra a
Fig. 3.63, na verdade corresponde a soma de três tipos de perdas já
comentadas:
ˆ
Somente perdas por histerese (curva azul, na Fig. 3.63).
ˆ
Perdas por histerese e correntes de Foucault (curva vermelha, na
Fig. 3.63).
ˆ
Perdas por histerese, correntes Foucault e excedentes (curva verde,
na Fig. 3.63).
A área da curva de histerese pode ser calculada pela solução da
integral
Z
w=
~ · dB
~
H
(3.97)
considerando
B = µH → dB = µdH,
(3.98)
137
Figura 3.63 Curva de histerese correspondente aos ciclos de perdas
do ferro: (a) perdas por histerese; (b) perdas por correntes de Focault;
(c) perdas excedentes.
Fonte:adaptado (GUERRA, 2010)
tem-se que:
Z
w=
H · µdH → w = µ
B2
BH
H2
=
=
[J/m3 ].
2
2µ
2
Considerando o volume do ferro
v = Slm ,
(3.99)
tem-se que a energia
é dada por
W =
Considerando que
3
142, 6 [cm ],
1
BHSlm .
2
lm = 0, 1686 [m], S = 84, 66 [cm2 ]
(3.100)
e
v =
da curva levantada experimentalmente obtemos a rela-
ção da energia por unidade de volume, multiplicado pelo volume do
138
ferro se obtém a energia dissipada no ciclo. Assim calculando a área
gracamente da curva de histerese obtida, temos que
W =
1
BHSlm = 0, 048 [J].
2
Para obter a potência por ciclo basta dividir a energia pelo tempo
correspondente de um ciclo ou simplesmente multiplicar pela frequência
0, 052 ∗ 60 = 3, 12 [W]
(erro 10%). Na simulação, utilizou-se a corrente
de vazio experimental de 52 mA o resultado apresentado 3,6 watt.
No caso da operação em vazio com uma corrente de pico de
52[mA] a energia acumulada foi de 10,6[mJ] na simulação.
Dos pontos do gráco da curva
BH
através de iterações obtemos
a área correspondente à energia para os valores máximos de indução
B0 = 0, 9544 [T]
e intensidade de campo
H0 = 337 [A/m]
na condição
corrente de vazio (52mA). Assim:
ˆ
Energia máxima =
ˆ
Coenergia = 168[J/m3] ( cálculo de coenergia realizado no gráco
B0 H0 = 322[J/m3]
( obtido da curva
BH ).
em Excel, através da técnica dos trapézios).
ˆ
Energia =322-168, obtendo a uma energia total de 154[J/m3]
Para calcular a potência do transformador nestas condições, basta
multiplicar por 60Hz.
Para determinar a potência de projeto teríamos que obter a energia acumulada no núcleo para a corrente nominal do primário acrescida
da corrente de vazio. No presente caso, a corrente de simulação foi de
367,7 mA (transferência) + 52 mA (magnetização + corrente de perda
núcleo). Para atingir a área máxima, é necessário fazer o transforma-
2
dor operar na condição acumulativa .
Realizando a simulação nesta
condição, obtém-se a energia no valor de 0,82 joule por ciclo. Essa informação indica que a potência máxima que o transformador poderia
fornecer, neste caso, é de de 50 W.
O transformador foi projetado segundo um roteiro proposto por
Alfonso Martingnoni (vericar Anexo C).
A potência de projeto se
encontra entre 50 VA e 57 VA dependendo dos fatores de laminação
considerados para a chapa (0.85-0,9) e dos fatores magnéticos
1, 3[T]
e
H = 140[A/m]
B =
do gráco. Assim, observa-se que poderia ser
2 A condição acumulativa ocorre quando os uxos de primário e secundário se
somam. Essa condição permite vericar a capacidade máxima de uxo possível no
interior do transformador. Na prática, porém, ocorre apenas a condição diferencial
(ou subtrativa), em que os uxos se contrapõem, respeitando a Lei de Lenz.
139
obtida uma potência aparente um pouco maior do que a prevista pelo
projeto, considerando o fator de potência.
3.11.1 Perdas por unidade de massa e volume
Através da curva de histerese foi possível determinar as perdas
sobre o volume de ferro, isto é, as perdas por unidade de volume do
material o que é muito útil para o projeto das máquinas, já que na
fase de projeto e simulação o volume do dispositivo é uma informação
disponível. Se a densidade do material da chapa é um dado conhecido
é possível determinar as perdas por kg de ferro, neste caso:
ˆ
Perdas por volume = 3,6 W/0,000142738m3 = 25[Kw/m3]
ˆ
Peso do transformador = 7900 kg/m3* 0,000142738m3 = 1,14[kg]
ˆ
Perdas por kg = 3,6W/1,14g = 3,2W/kg
A Tabela 3.6 apresenta valores usuais para perdas por unidade de
massa, em máquinas de corrente alternada, na condição de
g = 0, 5 [mm]
e
f = 50 [Hz],
B = 1 [T].
Tabela 3.6 Perdas por massa usuais em máquinas de corrente alternada
Qualidade da lâmina
Perdas por massa
Ausência de sílicio
3,6
Baixa concentração de silício
3,0
Alta concentração de silício
1,7
[W/kg]
(Alfonso Martignoni, Máquinas de Corrente Alternada).
3.11.2 Potência ativa por unidade de massa
Através da curva
BH
e a operação em condição acumulativa foi
possível determinar a energia acumulada sobre o volume de ferro. Esta
energia acumulada por ciclo permite o cálculo da potência máxima do
dispositivo.
Como é conhecido o volume e a densidade do material é possível
determinar a potência máxima associada à unidade de volume e de
massa, neste caso:
140
ˆ
Potência por volume = 50W/0,000142738 m
ˆ
Peso do transformador = 7900 kg/ m * 0,000142738m3 = 1,14 kg
ˆ
Potência por kg =50 W/1,14 kg = 46,5 W/kg
3
= 370 kW/ m
3
3
3
A densidade típica do ferro é de 7900 kg/ m , variando levemente segundo a liga formada.
3.11.3 Rendimento máximo
Ao dispor das informações de potência máxima e perdas máximas é possível estimar o rendimento do dispositivo. As perdas do ferro
e cobre por simulação resultaram serem próximas, usualmente no projeto de máquinas estes valores são próximos. Na simulação se obteve
a perda do ferro de 3,6 W e as perdas do cobre de 3,1W (condição
de projeto ótima no ferro e no cobre).
potência calculada no gráco
BH
Dessa forma, considerando a
(de 50 W), tem-se que o rendimento
máximo é a razão:
η=
50 − 3, 6
= 0, 87.
50 + 3, 1 + 3, 6
Isto é, com as características das chapas utilizadas só será possível obter um transformador com uma eciência máxima de 87%.
3.11.4 Ponto ótimo de operação
Através da caracterização do material no gráco de permeabilidade magnética percebe-se que o mesmo não está operando em seu
ponto "ótimo". O ponto ótimo de operação corresponde àquele de permeabilidade máxima, atingida com uma intensidade de campo de 100
A/m e uma indução magnética de 0,3 T, como mostra o gráco da
Figura 3.64.
Considerando um uxo magnético senoidal
φ = φm sin(ωt)
, a
expressão para a tensão de pico, considerando a Lei de Faraday, é dada
por:
p
Vpk = N φm ω = 220 (2)
A expressão para a densidade magnética máxima:
Bm =
Vpk
Vpk
→N =
→ N = 3620 [e].
N Sω
Bm Sω
141
Figura 3.64 Derivando a curva
BH
se obtém a curva de permeabili-
dade incremental, em que percebe-se que o ponto de menor relutância
coincide com uma intensidade de campo
H = 100 [A/m].
Fonte: Produção do Autor.
Da intensidade de campo
H,
através da lei de Ampere, obtém-se a
corrente de pico de 4,7 [mA ]. Os demais dados por consequência dos
quesitos de tensão e corrente no secundário são:
ˆ
Número de espiras primárias:
ˆ
Número de espiras secundárias:
ˆ
Material: Aço 1010;
ˆ
Relação transformação:
N1 = 3620 [e];
N2 = 394 [e];
a = 9, 17.
Simulando com estes parâmetros, se obtêm perdas no ferro de
0,336039 W. No caso do transformador sem otimização, para uma cor-
142
rente de pico de 20 [mA], a perda obtida no núcleo era de 3,6W, isto é,
11 vezes maior.
Com isso, verica-se que o número de espiras no projeto original
era de 1100, e aumentando 3 vezes este valor, as perdas são reduzidas
em mais de 11 vezes.
Logicamente, deve-se avaliar se na prática a factibilidade da
construção desse transformador ótimo, uma vez que o número de espiras é muito alto e a capacidade da janela do transformador é limitada.
3.11.5 Triângulo de potências
Para determinar a potência aparente na condição nominal será
utilizada a corrente de pico nominal acrescida da corrente de vazio:
I1 = 0, 3677 [A] + 0, 052 (vazio) = 0, 4197 [A],
a tensão nesta condição
foi de 220V, assim:
ˆ
ˆ
Potência aparente:
Potência ativa:
√
S1 = I1 V1 = 1/ 2 · 0, 4197 · 220 = 65, 3 [VA];
P1 = 53, 1 [W] (obtida a partir das características
BH );
magnéticas curva
ˆ
Potência Reativa:
Q1 = 38 [VAR];
ˆ
Fator de potência
F P = 0, 81.
Portanto, a eciência energética do pequeno transformador considerando seu rendimento e fator de potência é baixa, da ordem dos
70,5% (0, 87·0, 81). Isto se deve, neste projeto em particular, à corrente
de vazio, cujo valor se mostrou maior do que o tipicamente esperado
em relação à corrente nominal.
3.12 SEPARAÇÃO DAS PERDAS
Obtendo diferentes curvas de histerese utilizando a frequência
como parâmetro variável e mantendo constante a indução
B
f
é possível
utilizar o modelo de Steimetz e Bertotti para separar as perdas, montando um sistema de equações lineares de 3 variáveis correspondentes
aos coecientes de cada perda.
143
3.12.1 Perda de histerese
C.P. Steinmetz propôs uma fórmula empírica que permite calcular as perdas por histerese em função da indução máxima
Bm ,
no
material:
αh
Ph = Kh Bm
f,
em que
αh
(3.101)
pode variar entre 1,5 e 2 para induções de até 1,5[T].
3.12.2 Perdas por correntes parasitas (Foucault)
Esta equação foi modelada a partir das equações das correntes
induzidas de Faraday:
Pf =
pi2 2 2 2
2 2 2
B f e v → Pf = Kf Bm
f e v.
6ρ m
(3.102)
3.12.3 Perdas excedentes (modelo Bertotti)
Foi considerado o modelo de Bertotti para avaliar as perdas excedentes,
3
3
2
f 2.
PexcB = KexcB Bm
(3.103)
3.12.4 Aplicação do modelo de perdas
Foram realizados lenvantamentos do ciclo de histerese empregando o mesmo circuito descrito anteriormente nas frequências de 10,
50 e 60 Hz. Considerou-se uma indução magnética máxima
Bm =0,7 T.
Nessas condições, foi possível avaliar as perdas totais do ferro.
Com as perdas do ferro associadas às diferentes frequências, os
coecentes dos modelos de cada parcela podem ser determinados, resolvendo um sistema linear de
3×3
equações, com base no modelo
proposto:
3
3
2 2
αh
2
f 2 + Kf e2 vBm
f .
Pt = Kh Bm
f + KexcB Bm
(3.104)
144
Uma vez resolvido o sistema, considerando a espessura da chapa
3
0, 5
[mm] e o volume do material magnético 0,000142738 [ m ], são
obtidos os seguintes coecientes:
3
3
αh
2 2
2
Pt = 0, 0454Bm
f + 0, 00068Bm
f 2 + 4, 48 · 106 e2 vBm
f .
(3.105)
A Tabela 3.7 apresenta a distribuição percentual das perdas totais em função da indução e frequência. A simulação foi feita com a
corrente de 0,041 [A] que corresponde, segundo a curva
BH ,
a uma
indução de aproximadamente 0,8 [T].
Tabela 3.7 Perdas para diferentes frequências de operação, em [Hz].
A perda total simulada
Ps
e a perda total do modelo
Pe
são apresenta-
das em [W]. As parcelas de perdas dos modelos são expressas em [W]
e em %.
Nesse último caso, representa o quanto essa parcela contri-
bui percentualmente para as perdas do dispositivo em uma frequência
especíca.
f
Ps
Pm
Ph [W]
Ph %
Pexc [W]
Pexc %
PF [W]
PF %
60
2,29
2,34
1,74
74
0,22
9,4
0,34
14,5
50
1,86
1,88
1,45
77
0,17
9
0,26
13,8
10
0,317
0,32
0,29
90
0,015
4,7
0,0102
3,2
Da Tabela 3.7 se pode armar que, na faixa de frequências utilizadas na indústria, as perdas por causa da histerese são muito signicativas e tendem a aumentar proporcionalmente quando a frequência
diminui. Utilizando o modelo de histerese na frequência de 1 [Hz] se
obteve uma perda da ordem dos 98%, na simulação. Conclui-se que a
eciência das máquinas está fortemente atrelada às perdas de energia
nos domínios magnéticos. Como foram apresentados na parte introdutória, os vidros metálicos parecem ser promissores.
145
Figura 3.65 Curva de histerese traçada a 10 Hz, por métodos grá-
3
cos se obteve uma densidade de energia de 30[J/ m ], corresponde a
uma potência de 0,32 watt. Segundo a literatura as irregularidades no
contorno podem ser causa dos saltos de Barkausen, embora existe a
possibilidade de uma contaminação com ruído, o qual se torna notório
em baixas frequências.
Fonte: Produção do Autor.
Do gráco da Figura 3.66 se percebe que as perdas por correntes
parasitas tornam-se maiores em frequências próximas a 300 Hz, esta
é a frequência máxima que pode operar um inversor, neste caso a estratégia mais rentável é diminuir a condutividade do material, no caso
dos materiais amorfos, isto se consegue pela adição de Boro e silício.
Observar também Figuras 3.65, 3.67 e 3.68 para melhor compreensão
desses fenômenos.
146
Figura 3.66 Separação perdas em função da Indução.
Fonte: Produção do Autor.
Figura 3.67 Operação em regime quase estático: as perdas de histerese
são muito próximas das perdas totais.
Fonte: Produção do Autor.
147
Figura 3.68 Separação das perdas em função da frequência.
Fonte: Produção do Autor.
3.13 CORRENTE DE
IN-RUSH
Os parâmetros levantados anteriormente serão utilizados para
modelar a corrente de
in-rush
do transformador.
Esta corrente apa-
rece durante a energização do transformador, devido à magnetização
e à saturação do seu núcleo, sendo sua magnitude determinada pela
declividade da característica de magnetização na região saturada.
rush
Nos transformadores de elevada potência, altas correntes de
in-
podem ser atingidas.
Os transformadores usados nos sistemas elétricos de potência
requerem, em regime permanente, correntes de excitação da ordem de
0,5% a 2% da corrente nominal.
3.13.1 Comportamento em regime não-saturado
O circuito RL da Fig. 3.69 destina-se ao estudo do transitório
de corrente durante a energização de um transformador monofásico por
fonte de tensão senoidal, com o secundário em aberto. O indutor nãolinear indicado possui característica de magnetização
i = f (λ),
onde
λ
148
Figura 3.69 Circuito não-linear para representação de um transformador com secundário em vazio.
Fonte: adaptado de (GUERRA, 2010)
é o uxo de enlace no primário. Inicialmente, são desprezadas as perdas
no núcleo. Após o fechamento da chave, tem-se:
dλ
+ Ri = Um sin(ωt)
dt
Como a relação
i = f (λ)
(3.106)
é não-linear, a Equação (3.106) só
poderá ser resolvida numericamente. Entretanto, se for assumido que
o núcleo magnético não atinge a saturação, pode-se fazer
λ/Lm , onde Lm
i = f (λ) =
e a indutância de magnetização do transformador, que
corresponde a inclinação da reta que passa pela origem e pelo ponto de
joelho da curva
Para
λ − i;
assim, (3.106) pode ser escrita como:
dλ
+ R/Lλ = Um sin(ωt)
dt
simplicar, supõe que λ(0) = 0; assim,
(3.107)
esta equação tem
por solução:
λ(t) =
ωL2m Um
R
ωL2m Um
−(R/Lm )t
e
+
sin
ωt
−
cos
ωt
R2 + (ωLm )2
R2 + (ωLm )2 ωLm
(3.108)
Considerando
R ωLm
e fazendo
λm = Um /ω ,
λ(t) = λm [e−(R/Lm )t − cos ωt]
resulta
(3.109)
A solução desejada é composta por duas partes fundamentais: a
solução particular e a solução complementar.
149
O primeiro representa o regime permanente e o segundo é o termo
transitório.
A equação (3.109) é composta por um termo com decaimento
exponencial, relacionado ao comportamento transitório de
λ
logo após
a aplicação da tensão, e por um termo senoidal relacionado ao regime
permanente. A Fig. 3.70 mostra a variação de
λ logo após a energização
do transformador.
Figura 3.70 Fluxo de enlace em função do tempo logo após a energização do transformador.
Fonte: adaptado de (GUERRA, 2010)
Um fator de importância fundamental no grau de assimetria da
onda de uxo é o valor da tensão da fonte no momento da energização
do transformador.
u = Um sin ωt, de modo que u(0) =
u(0) 6= 0. A seguir, é
u = Um sin(ωt + θ), o que implica ter u(0) = Um sin θ,
Na análise anterior, fez-se
0.
Porém, o caso mais comum ocorre quando
considerado
onde
θ, denominado angulo de chaveamento, determina o valor inicial
da tensão.
Caso haja interesse em apenas avaliar o valor de pico inicial
de
λ,
o amortecimento nos instantes subsequentes pode ser ignorado.
Fazendo
R=0
no circuito da Fig. 3.69, se obtêm:
dλ(t)
= Um sin(ωt + θ)
dt
Considerando
λ(0) = λR
e
λm = Um /ω ,
(3.110)
resulta
λ(t) = λR + λm [cos(θ) − cos(ωt + θ)]
(3.111)
150
A onda de uxo no núcleo apresenta valor máximo quando
kπ(k = 1, 3, .5, ...)
e
θ = 0,
ωt =
caso em que a tensão da fonte é nula no
instante da energização. Assim, o máximo valor de
λ
é
λR + 2λm . Por
λ para λR = 0
de pico Um em
outro lado, não ocorre assimetria na forma de onda de
θ = π/2, situação em que a tensão assume o valor
t = 0. Esta é a condição mais favorável, pois são evitados
e
sobreuxos
que poderiam levar o núcleo a saturação.
Devido ao termo transitório, pode-se observar um fenômeno constatado por Fleming em 1892.
O fenômeno observado mostrou que
quando um transformador é conectado à rede, por vezes há o aparecimento de uma grande corrente transitória de magnetização.
O efeito da referida corrente é causar momentaneamente uma
queda de tensão alimentadora e uma possível atuação de relés instantâneos ou relés diferenciais. O valor atingido nesse regime transitório
depende de dois fatores:
ˆ
ponto do ciclo da tensão, no qual a chave para o energizamento
seria fechada;
ˆ
condições magnéticas do núcleo, incluindo a intensidade e polaridade do uxo residual.
Para um pequeno aumento de uxo no núcleo, necessita-se uma grande
corrente (devido ao fenômeno da saturação, conforme Figura D.3, presente no Anexo D), denominada de
in-rush
ou corrente de avalanche.
3.13.2 Comportamento em regime saturado
Durante os primeiros instantes da energização de um transformador, os elevados valores de uxo atingem a região de saturação do
laço de histerese do núcleo. Assim, para pequenas variações de
λ,
po-
dem ocorrer variações muito elevadas de i, de modo a se estabelecer um
surto de corrente. Isto pode ser entendido mediante análise da Figura
3.71.
No caso anterior, a característica
λ
versus
i
do núcleo foi re-
presentada pela curva de saturação (relação biunívoca correspondente
a uma curva que passa pela origem), o que não permite considerar a
existência de uxo residual ou remanescente.
cia do uxo residual
λR
nos valores de
i,
Para avaliar a inuên-
considera-se o núcleo com
histerese.
Como a excitação é assimétrica, a trajetória descrita no plano
apresenta laços menores também assimétricos.
λi
151
Figura 3.71 Fluxo de enlace e corrente de
in-rush
em um transforma-
dor.
Fonte: adaptado de (GUERRA, 2010).
Como
λ acha-se limitado pelo nível de saturação, λS ,
não é alcançado.
o valor
λm
Observa-se que, se o uxo residual no núcleo apre-
sentar mesmo sinal do uxo imposto pela fonte, a região de saturação
pode ser atingida mais rapidamente, com maior intensidade, resultando
em maior assimetria da onda de uxo e em valores de pico de corrente
de
in-rush
mais elevados. Por outro lado, se os citados uxos apresen-
tarem sinais contrários, a corrente de
in-rush
será atenuada. Frente a
estas situações de uxo residual, é possível a ocorrência de seis situações
"fortuitas":
1. Energização com tensão em 0 Volt e sem magnetismo residual;
2. Energização com tensão em 0 Volt e máximo magnetismo residual
com polaridade oposta ao uxo normal;
3. Energização com tensão em 0 Volt e máximo magnetismo residual
com mesma polaridade do uxo normal;
4. Energização com máxima tensão e sem magnetismo residual;
5. Energização com máxima tensão e máximo magnetismo residual
com polaridade oposta ao uxo normal;
152
Tabela 3.8 Percetual de hamônicos de corrente utilizados por relés
diferenciais para evitar disparos desnecessários.
Harmônico
% Em relação à fundamental
2H
63%
3H
26,80%
4H
5,10%
5H
4,10%
6H
3,70%
7H
2,40%
6. Energização com máxima tensão e máximo magnetismo residual
com mesma polaridade do uxo normal.
As correntes de
in-rush
podem fazer com que relés de proteção
de operação rápida atuem de modo indevido durante a energização
do transformador.
Para evitar que isto ocorra, os relés diferenciais
utilizam um critério capaz de distinguir uma corrente de
uma corrente de curto-circuito.
in-rush
se baseia na avaliação do conteúdo de harmônicos da corrente.
corrente de
in-rush
de
O critério tradicionalmente utilizado
Uma
típica apresenta uma composição de harmônicas
onde predomina a harmônica de segunda ordem, que pode representar
mais de 60% do valor da componente fundamental. Assim, quando o
transformador é energizado em condições normais, essas harmônicas
são ltradas, exercendo uma ação de bloqueio que evita a operação do
relé. A Tabela 3.8 apresenta os valores comparativos utilizados pelos
relés.
Por outro lado, as correntes de curto-circuito típicas são normalmente compostas por uma componente fundamental acrescida de uma
componente contínua com decremento exponencial, sendo o conteúdo
de harmônicos insignicante em comparação com os observados nas
correntes de
in-rush.
Assim, não se verica a ação de bloqueio no sentido de impedir
a operação do relé.
3.13.3 Características de uma corrente de
in-rush
Entretanto, durante o processo de energização ( transitório), podem ocorrer surtos de corrente com as seguintes características:
153
ˆ
valor de pico inicial que pode superar vinte vezes o valor de pico
da corrente nominal, nas condições mais severas;
ˆ
duração de vários ciclos;
ˆ
amplo espectro de harmônicos que inclui componentes de ordem
par, predominando a segunda harmônica.
3.13.4 Os principais efeitos das correntes de
tema
Os principais efeitos das correntes de
in-rush
in-rush
num sis-
sobre um sistema
elétrico, no caso de transformadores de potência são descritos a seguir:
ˆ
atuação indevida de fusíveis e relés de proteção;
ˆ
afundamentos temporários de tensão, com deterioração da qualidade de energia;
ˆ
solicitações de natureza eletromecânica e térmica no transformador e nos demais componentes do sistema, o que incorre em redução de vida útil;
ˆ
sobtensões causadas por fenômenos de ressonância harmônica em
sistemas que contem ltros elétricos (sistemas industriais e linhas
de transmissão em corrente contínua).
3.13.5 A intensidade e a duração das correntes de
in-rush
A ordem de grandeza e a duração deste efeito afetam a operação
e conabilidade de um sistema de potência, sua amplitude e tempo
dependem dos seguintes fatores:
ˆ
valor instantâneo da tensão aplicada ao transformador no instante
da energização;
ˆ
magnitude e sinal do uxo residual no núcleo magnético;
ˆ
resistência e indutância equivalentes em série do circuito alimentador;
ˆ
resistência e indutância de dispersão do enrolamento primário do
transformador;
ˆ
velocidade de fechamento dos contatos do disjuntor.
154
3.13.6 Modelo de transformador monofásico
O circuito da Fig.
3.72 ilustra o processo de chaveamento de
um transformador monofásico com o secundário em aberto. Para este
circuito, pode-se escrever:
dλ(t)
+ Ldi(t)dt = u
dt
(3.112)
dλ(t)
dλ(t)
+ Ldi(t)dλ
+ Ri = u
dt
dt
(3.113)
Figura 3.72 Circuito considerado para o cálculo da corrente de
rush.
in-
Fonte: adaptado de (GUERRA, 2010).
dλ(t)
u − Rf (λ)
=
dt
1 + L/Lm
A condição inicial e
λ(0) = λR
(3.114)
(uxo residual no núcleo antes
da energização).
3.13.7 Representação da histerese
Ha determinados estudos relacionados a transformadores onde
o efeito de histerese no núcleo magnético pode ser desprezado, sendo
suciente representar a relação
i = f (λ)
do material pela curva de
saturação. Isto ocorre em estudos de fenômenos transitórios, onde são
alcançados graus de saturação elevados (como e o caso do fenômeno de
155
in-rush ) e a remanência é pequena ou não constitui objeto de interesse
da análise.
Porém, ao se representar a característica de magnetização do
núcleo em termos da curva de saturação, não é possível se considerar
valores de uxo residual diferentes de zero no instante da energização.
Isto se deve ao fato de que o lugar geométrico descrito no plano
λi
consiste em uma curva singular que passa pela origem.
O problema pode ser resolvido mediante consideração do efeito
de histerese (uxos residuais).
Diversos modelos de histerese foram
desenvolvidos, alguns fundamentados em leis físicas (JILES; ATHERTON, 1986; NAIDU, 1990) outros baseados em observações experimentais (FRAME; MOHAN; LIU, 1982). Como não é necessário representar o efeito de histerese com grau de precisão muito elevado no cálculo
das correntes de
in-rush,
o impasse pode ser resolvido através da uti-
lização de modelos com formulação simples, os quais permitam que o
uxo residual seja levado em consideração.
3.13.8 Curva BH do material ferromagnético do núcleo
Inicialmente, realizou-se o levantamento das características de
um transformador e a partir da curva de histerese traçada através de
um osciloscópio digital levantando 500 pontos de amostras.
A curva
BH
do material ferromagnético do núcleo foi obtida
experimentalmente e é apresentada na Figura 3.73.
3.13.9 Resultados experimentais
Utilizando um resistor shunt de 10
[Ω] para obter a forma de onda
da corrente, no regime transitório a corrente atinge um valor máximo
de 1,3 [A]. Em regime permanente, o valor máximo obtido foi de 55
[mA]. A relação entre a corrente de regime permanente e a de
é de:
iin-rush =
in-rush
1, 3[A]
= 23, 63.
55[mA]
Desse modo, constata-se que a corrente de
in-rush
é 24 vezes maior que
a corrente de regime do transformador.
Através de um gráco de tendências (conferir Figura 3.75), é
possível estimar o número de ciclos do transitório (conferir Figura 3.76).
156
Figura 3.73 Curva
BH
do material obtida através de uma amostragem
de 500 pontos.
Fonte: Produção do Autor.
3.13.10 Resultados das simulações
A corrente de
in-rush
aparece como consequência de um uxo
residual, que se encontra em quadratura com a tensão aplicada, matematicamente é possível compreender através da lei de Faraday:
Vt = −N
sendo
dφ
,
dt
(3.115)
φ(t) = φm sin(θ).
Assim, quando o transformador é novamente energizado, numa
condição particular, estes uxos podem somar seus efeitos, aumentando
a indução
B
o que por sua vez aumenta a intensidade de campo
H,
e,
consequentemente, a corrente de vazio do transformador.
Se o transformador é religado na condição
V (t) = 0
(pior caso),
num curto intervalo, os uxos residual e máximo se somam, duplicando
o valor máximo da indução
B.
157
Figura 3.74 Corrente transitória
in-rush
de valor máximo 1,3 [A]. O
transitório se mantém por 20 ciclos de rede aproximadamente.
Fonte: Produção do Autor.
Figura 3.75 Tendências da corrente de
in-rush.
Fonte: Produção do Autor.
Se o transformador é ligado em forma sucessiva, estes uxos residuais começam a se somar devido ao fato de que o transitório é muito
lento.
Neste caso, o transitório dura em torno de 20 ciclos de rede.
158
Figura 3.76 A corrente de pico na condição permanente atinge um
valor máximo de 55 mA.
Fonte: Produção do Autor.
Para determinar o uxo máximo que pode ser atingido na condição
de saturação máxima, o transformador será simulado na condição de
uxos aditivos e não em condição diferencial, que é o caso natural de
operação (observar Figura 3.77).
Figura 3.77 Linhas de uxo no transformador simulado.
Fonte: Produção do Autor.
A intensidade de campo nesta condição é
a densidade magnética
B = 5 [T]
H = 5200 [Ae/m]
e
aproximadamente, a corrente nesta
condição pode ser calculada pela lei de Ampere:
159
Hlm = N i => i =
5200 [Ae/m] × 0, 1686
= 0, 800 [A],
1100 [e]
o que corresponde a uma corrente 15 vezes maior que a corrente de
vazio de projeto.
Experimentalmente, encontrou-se um valor para a corrente de
in-rush
de 24 vezes a corrente de vazio. A diferença se deve ao fato que
a corrente de
in-rush
é a soma das correntes de saturação do núcleo
mais a corrente gerada pelo efeito de uma indutância de magnetização
de um valor muito pequeno, assim
L = Lm ≈ 0
(lembrando que a
indutância é proporcional a permeabilidade diferencial, ver gráco da
Figura 3.42). Isto é, as indutâncias se tornam curtos, transformado o
circuito equivalente do transformador da Figura 3.72 em uma resistência equivalente, que representa as perdas do cobre e ferro.
A Tabela 3.9 apresenta resultados da simulação na condição de
operação aditiva que leva à saturação o núcleo.
Tabela 3.9 Resultados da simulação no FEMM.
Corrente total
0,4197 Ampere
Queda de tensão
= 230,779+j 1578,91 Volt
Fluxo concatenado
4,18819-j 0,600128 Weber
Fluxo por corrente
9,97901-j 1,4299 Henry
549,865+j 3762
Impedância
Potência ativa
Ω
48,4289 Watt
Potência reativa
331,334 VAr
Potência aparente
334,855 VA
A corrente na condição onde a indutância de magnetização é
muito pequena:
ir1 =
311
= 0, 565 [A].
550
Dessa maneira, o valor teórico que a corrente de
seria de:
irush = isat +ir1
corrente de
in-rush
in-rush atingiria
= 0,8[A] +0,565[A] = 1.365[A]. Entretanto, a
obtida de forma experimental foi de 1,3[A]. Assim,
o erro entre o modelo desenvolvido e o valor experimental foi de 5%.
160
3.13.11 Considerações sobre os resultados do modelo para a
corrente de in-rush
Através da caracterização do material do núcleo ferromagnético
foi possível estimar as correntes de saturação magnética, simulando o
transformador na condição aditiva. A corrente de saturação magnética
torna a indutância de magnetização
Lm
um valor muito pequeno, per-
mitindo assumir uma condição de curto circuito. Desse modo, o modelo
indica apenas a existência de uma resistência equivalente, correspondente as perdas geradas no cobre e no núcleo que pode ser obtida da
simulação. Isso explica os elevados valores transitórios da corrente de
in-rush.
Foi possível, assim, validar o modelo do transformador desenvolvido com os dados da caracterização do material, através da obtenção
teórica da corrente de
in-rush.
O erro obtido foi de 5%, comprovando
a validade do modelo de simulação gerado através da caracterização do
transformador.
3.14 CONSIDERAÇÕES FINAIS DO CAPÍTULO
Neste capítulo, foi realizado um estudo aprofundado de um dispositivo magnético sem entreferro, o transformador monofásico. O estudo inicialmente concentrou-se em determinar um modelo de perdas
para o dispositivo, através das características dos materiais magnéticos.
A partir disso, o enfoque do estudo foi a curva de perdas do ferro,
também conhecida como curva de histerese, e, dessa, a curva
BH
do
material.
Essa curva permitiu o desenvolvimento de um modelo aprofundado do transformador, com a obtenção de todos os seus parâmetros
magnéticos. Constatou-se que, tal qual a própria curva, todos apresentavam características não lineares, dependentes da corrente de excitação.
Uma vez obtidos os parâmetros, no ponto de operação nominal
do transformador, foi possível fazer a avaliação de perdas, conforme
o modelo estudado inicialmente.
Os parâmetros foram obtidos por
diversos métodos, de modo que a Tabela 3.10 apresenta uma síntese
dos resultados obtidos.
Por m, foi realizada a validação desse modelo no estudo de um
fenômeno ímpar dos transformadores: a corrente de
in-rush.
161
Tabela 3.10 Síntese dos cálculos de indutância no ponto de operação
do transformador.
Método
L1
I0 = 23, 19 + j46, 9,
I2 = aI10 = 0, 5972
Para os cálculos, considerar
I10 = 65, 13, I1 = 88, 32 + j46, 9
[H]
L2
e
[H]
LM
[H]
l1
[mH]
l2
[mH]
K
Fluxo
8,643
0,158
0,942
13,5
0,066
0,81
Gráco
8,236
0,098
0,903
0,15
0,0018
1,0
8,643
0,158
0,851
839
65
0,73
11,720
0,055
0,800
12,7
0,0678
0,98
Energia
Experimental
Seguem apenas algumas considerações a respeito das discrepâncias observadas na Tabela 3.10.
Na obtenção da curva BH a partir da curva de histerese, a corrente associada as perdas do ferro já estavam implícitas, gerando um
erro no gráco BH o qual deveria ser traçado só com a corrente de
magnetização
Ix
(Figura 3.78). A curva
BH
por sua vez afeta o com-
portamento da permeabilidade do material. O resultado nal disto é
um erro aditivo nos diferentes métodos com relação ao método experimental (observar Figuras 3.79 e 3.80).
Figura 3.78 Modelo do núcleo na obtenção da curva de magnetização.
162
Figura 3.79 Correção na curva BH experimental em função da corrente associada as perdas do ferro.
Figura 3.80 A diferença nas curvas de indutâncias primaria
L1
teó-
rica e experimental é produzida pela corrente de vazio. Essa corrente
afeta a curva
BH
e, consequentemente, a permeabilidade absoluta do
material. Outro efeito dessa corrente é a redução da relação de transformação. Isso diculta signicativamente o processo de determinação
das indutâncias de dispersão primária e secundária.
163
A corrente primária corresponde a soma fasorial da corrente de
vazio e a corrente primaria
transformação
a
i01 ,
a qual é multiplicada pela relação de
para obter a corrente secundaria
i2
(conforme Figura
3.81).
Figura 3.81 Modelo de núcleo com correntes de compensação.
Desse modo:
→
−
→
−
i2 = i01 a
Assim a corrente
I10 :
→
−0
→
− →
−
i1 = i1 − io
onde
→
−
→
− →
−
io = ir − ix
Como conseqüência disto a relação
Figura 3.82.
a =
i2/i1 , segue a curva da
164
Figura 3.82 Variação na relação de transformação por efeitos da corrente de vazio
I0 ,
o transformador atinge seu valor de projeto, neste
caso de 9.17, com uma corrente iguais ou superior a nominal. Os valores
experimentais estão indicados com 'x'.
Nesta curva, percebe-se que a relação passa a ser constante próxima do valor nominal da corrente primária, isto é, com uma corrente
em torno do 30% da nominal os erros tornam-se grosseiros.
No caso de transformador com núcleos de ar, onde a permeabilidade relativa é unitária, não existiria esse problema, em função da
corrente de magnetização.
No próximo capítulo, é realizado um estudo de dispositivos com
entreferro variável.
165
4 CARACTERIZAÇÃO DE UM
CONTACTOR CA
Com base nas limitações da análise clássica do circuito magnético, o capítulo aborda a utilização, em conjunto, da análise de elementos nitos e o princípio da dualidade entre circuitos elétricos e
magnéticos. O dispositivo utilizado na derivação de circuitos elétricos
equivalentes e modelos de elementos nitos é um contactor de corrente
alternada (AC) de tensão nominal de 220 volt, 60 hertz.
Duas con-
dições de funcionamento são consideradas: a manobra de fechamento
bloqueado e a conguração de núcleo fechado.
A metodologia utilizada no Capítulo 3 para caracterizar um
transformador pode ser facilmente aplicada a dispositivos com entreferros variáveis como é o caso de um contactor.
Neste capítulo, apresenta-se a sequência que permite caracterizar materiais com entreferro especíco.
Com a geometria e os dados
experimentais do dispositivo, são geradas as diferentes curvas características, necessária para avaliar o desempenho do dispositivo, tendo em
vista a eciência energética.
4.1 OBJETIVOS
O presente capítulo contempla os seguintes objetivos:
ˆ
apresentar uma sequência para projetar e avaliar o desempenho
de um dispositivo com entreferro variável. O ponto de partida é
a caracterização do material magnético. Para isso, é utilizado um
circuito simples e de baixo custo, que permite obter um gráco
das perdas de ferro (curva de histerese).
Com esta informação
e com a geometria do dispositivo, podem ser derivadas todas as
curvas necessárias que permitem obter os parâmetros elétricos
e magnéticos, para diversas correntes de operação.
Os cálculos
dos parâmetros de interesse são feitos via teoria eletromagnética
clássica e pelo método gráco e o erro é avaliado utilizando os
resultados da simulação como referências;
166
ˆ
obter o fator de potência e rendimento do dispositivo, utilizando
a energia e coenergia calculada na curva BH através de programas
como Excel e Matlab;
ˆ
apresentar uma técnica gráca que englobe uma visão qualitativa de fenômenos complexos de eletromagnetismo, de forma que
sejam úteis em práticas didáticas;
ˆ
compreender o efeito dos entreferros nas máquinas, as alterações
na curva BH e os cálculos de força associados.
4.2 DESCRIÇÃO DO PROBLEMA
O eletroímã presente em um contactor é um componente que
afeta diretamente sua ação em termos de produção de força e que é
determinante no processo de fechamento do contactor. O eletroímã do
contactor em estudo contém uma bobina contendo aproximadamente
5.000 espiras. Essa bobina está enrolada em torno da trave central do
núcleo laminado e em forma de "E", formando a porção estacionária
do contactor. Para a conguração de núcleo fechado, cada janela retangular do núcleo tem uma altura de 3,2 cm e uma largura de 1,05
cm. A altura da bobina é de 1,4 cm, aproximadamente. As partes que
compõem o eletroímã, juntamente com as principais dimensões geométricas, estão indicadas na Figura 4.1. A profundidade do dispositivo é
de 1,2 cm.
O contato físico entre os dois núcleos magnéticos em forma de
"E"está restrito a pequenas regiões localizadas nas traves laterais. A
parte mais interna das superfícies magnetizadas em contato é conhecida
como polo não sombreado. As regiões adjacentes também têm contato
com a porção superior, móvel do núcleo.
Tais regiões são envolvidas
por espiras em curto-circuito e são conhecidas como polos sombreados.
Uma ilustração representativa dessas regiões pode ser vista na Figura
4.2.
A distância que separa as duas traves centrais dos núcleos desse
eletroímã é de 8,0 mm quando o contactor está aberto e, apenas 0,4 mm
quando o mesmo está fechado, como está indicado na Figura 4.3. Na
Tabela 4.1 estão indicados dados geométricos adicionais referentes ao
núcleo na conguração do contactor em que as duas seções do núcleo
estão em contato físico (contactor fechado).
Esses dados são empre-
gados nos cálculos analíticos. O comprimento médio de circulação do
uxo magnético, lm , é empregado nos cálculos envolvendo a lei circui-
167
Figura 4.1 Dimensões do contactor em estudo.
Fonte: adaptado de (NOGUEIRA; PEREIRA JR, 2006)
tal de Ampère e está representado pela linha tracejada que aparece na
Figura 4.3. Nos cálculos analíticos, assume-se que a seção magnética
do núcleo,
Sn ,
é igual à área de uma das traves laterais do contactor.
Também, na Tabela 4.1, estão indicadas as dimensões geométricas da
espira de sombra do contactor.
Tabela 4.1 Dados geométricos do núcleo magnético, contactor fechado.
Comprimento médio de circulação do uxo
Seção magnética do núcleo
Espira de sombra
11,6 cm
126 · 10−6 m2
Comprimento 13,0 mm
Largura
5,0 mm
Altura
1,6 mm
Espessura
1,0 mm
168
Figura 4.2 Sombreamento dos polos.
Fonte: adaptado de (NOGUEIRA; PEREIRA JR, 2006)
Foram estudadas as relações eletromagnéticas e o princípio de
conversão eletromecânica de um contactor, o qual corresponde a um
eletroímã com entreferro variável acoplado à parte móvel. A Figura 4.4
apresenta a vista frontal do contactor em estudo.
O contactor em questão é formado por dois núcleos em "E" iguais,
como ilustrado na Figura 4.5. Um deles está na parte xa do contactor
e o outro faz parte do conjunto móvel.
Um detalhe importante na construção do contactor CA é a utilização de uma espira sombreada, conforme apresentado na Figura 4.5. A
Figura 4.6 apresenta o contactor modelado no sistema CAD do FEMM.
4.2.1 Determinação experimental do número de espiras da bobina
Diferentemente do caso do transformador, em que o número de
espiras era dado por condições de projeto, no caso do contator é necessário se desenvolver uma metodologia para este m.
169
Figura 4.3 Contorno utilizado para realização dos cálculos.
Fonte: adaptado de (NOGUEIRA; PEREIRA JR, 2006)
A base teórica dessa metodologia é a lei da indução de Faraday,
em sua forma simplicada. Com o contactor fechado e alimentado com
tensão nominal ecaz,
Vn ,
de 220 V, mede-se a tensão induzida E nos
terminais do enrolamento de uma bobina de 4 espiras alocada no núcleo.
De acordo com a lei de Faraday, tem-se
E = Nc
onde
φ
(4.1)
denota o uxo magnético que circula nas traves laterais do
contactor e
seja,
dφ
dt
Nc = 4
Nc
denota o número de espiras do enrolamento extra, ou
(conferir Figura 4.7).
170
Figura 4.4 Vista frontal do contactor em estudo.
Fonte: Produção do Autor.
Figura 4.5 Parte xa do contactor.
Fonte: Produção do Autor.
O valor ecaz da tensão medida nos terminais da espira é de
176 [mV].
A taxa de variação do uxo é numericamente igual à queda
de tensão em uma única espira,
dφ
E
=
= 44 mV/espira.
dt
Nc
171
Figura 4.6 Contactor implementado no FEMM.
Fonte: Produção do Autor.
O procedimento de cálculo assume que a "queda de tensão por
espira" é a mesma no enrolamento principal da bobina excitadora e no
enrolamento extra. Para uma tensão terminal de 220 V no enrolamento
principal, o número de espiras,
Ne ,
Ne =
desse enrolamento é
Vn
.
dφ/dt
(4.2)
Substituindo os valores, tem-se
Ne =
220
Vn
=
= 5000 espiras.
dφ/dt
0, 044
4.2.2 Tensão e corrente experimentais na espira de sombra
Para determinar a tensão induzida na espira, construiu-se uma
bobina de 6 espiras e mediu-se a tensão induzida, neste caso de 73mV.
Essa tensão corresponde a uma tensão por espira de 0,012V (observar
Figura 4.8 que apresenta a bobina utilizada para a avaliação da corrente
na espira de sombra).
172
Figura 4.7 Bobina de espiras conhecidas para determinar a tensão
induzida por espira.
Fonte: Produção do Autor.
Em teoria, seria necessário apenas uma espira na bobina auxiliar,
para identicar a relação de tensão gerada. Entretanto, para melhorar
a medição usualmente são utilizadas 10 espiras.
Com isso, a tensão
induzida, geralmente da ordem de milivolt, aumenta para ordem de
volt e, dessa forma, a precisão também se eleva.
Utilizaram-se bobinas de 4 e 6 espiras por questões de espaço no
dispositivo em função das bitolas de os de que estavam disponíveis. O
ideal, porém, teria sido 10 espiras em cada caso.
S =
= 13 + 5 + 13 + 5 = 36 [mm] e
= 0, 0175[ Ωm/mm2] é possível calcular a
Através da geometria, considerando a seção transversal
1, 6 × 1 [mm2 ],
o comprimento médio lm
a resistividade do cobre
ρcu
resistência da espira:
R=
ρcu lm
= 0, 328 mΩ.
S
173
A corrente na espira
Ie =
12 mV
= 37 A.
0, 328 mΩ
A Figura 4.9 apresenta um diagrama ilustrativo sobre os uxos
gerados pela bobina principal e pela espira de sombra.
Figura 4.8 Montagem da bobina de espiras conhecidas que permite
avaliar a tensão por espira.
Fonte: Produção do Autor.
174
Figura 4.9 Diagramas dos uxos gerados pela bobina principal e a
espira de sombra.
Fonte: adaptado de (NOGUEIRA; PEREIRA JR, 2006)
4.3 DETERMINAÇÃO DAS CARACTERÍSTICAS MAGNÉTICAS DO NÚCLEO
O material usualmente utilizado em máquinas elétricas é ferrosilício. O silício melhora as propriedades magnéticas do ferro fazendo
que se oriente rapidamente e mantenha baixo seu magnetismo residual.
Diversos fabricantes têm desenvolvidos diferentes tipos de ferros com
adição de silício.
No caso de ferro para acionamentos, a série vai do
Carpenter Silicon Iron até M-45. Neste caso, foi utilizada a liga chamada de Carpenter. A curva
BH
do material a vazio é apresentada na
Figura 4.10.
No estudo realizado nesse trabalho, a inclinação e o nível de
saturação foram muito inuenciados por um entreferro minúsculo de
0, 4 mm
do núcleo. Para compreender seu efeito sobre o acionamento
foi levantada a curva
BH
especíca do dispositivo através de métodos
semelhantes aos descritos no Capítulo 3, para a condição de entreferro
de 0,4mm. Essa curva é exibida na Figura 4.11.
175
Figura 4.10 Material Carpenter Silicon Iron da biblioteca do Femm.
Fonte: Produção do Autor.
Figura 4.11 Material Carpenter Silicon Iron com entreferro de 0,4mm.
Fonte: Produção do Autor.
A subseção 4.3.1 detalha o procedimento de obtenção da curva
BH
apresentada na Figura 4.11.
176
4.3.1 Circuito proposto para levantar a curva de histerese
No caso especíco de um contactor ou qualquer dispositivo só
com uma bobina o circuito proposto é uma variante daquele utilizado
para caracterizar o transformador (conferir Figura 4.12).
Figura 4.12 Circuito proposto para dispositivos com uma única bobina
de excitação.
Fonte: adaptado de (NOGUEIRA; SALAS, 2013)
No caso,
B(t).
Vx (t)
é proporcional a
H(t)
e
Vy (t)
é proporcional a
Essas duas tensões são lidas pelos canais 1 e 2 do osciloscópio.
A operação no modo
xy
(com o canal 1 relacionado ao eixo
característica de histerese
B(t) = f (H(t))
x)
exibe a
do núcleo magnético.
4.3.2 Fatores de escala
O circuito da Figura 4.12 apresenta só as tensões que são proporcionais à indução
B(t)
e a intensidade de campo
H(t).
Para obter os
valores dos campos, é necessário multiplicar estas tensões por fatores de
escalas, de forma semelhante a observada no estudo do transformador.
H(t) =
N
Vx → H(t) = 4310Vx
lm Rsh
177
H(t) =
RC
Vy → B(t) = 0, 208Vy
NS
A Tabela 4.2 apresenta os parâmetros do circuito apresentado
na Figura 4.12.
Tabela 4.2 Parâmetros do circuito de excitação.
lm
Rsh
R
C
S
0, 116 m
10 Ω
100 kΩ
1, 5 µF
12 × 12 mm2
4.3.3 Formas de onda da tensão (B ) e corrente (H ) em função
do tempo
As formas de onda obtidas apresentam uma tensão senoidal cor-
B e uma corrente distorcida correspondente à
H . Embora a corrente ainda continue distorcida
respondendo à indução
intensidade de campo
seu conteúdo harmônico é muito menor considerando às formas de onda
da corrente de vazio do transformador, graças à presença do entreferro
(conferir Figura 4.13).
4.3.4 Curva de histerese
Através de fatores de escala previamente calculados, pode-se obter o gráco da curva de histerese, que representa não apenas o fenômeno da histerese magnética em si, mas também todas as perdas do
ferro, como as correntes de Foucault e as perdas anômalas.
A curva de histerese obtida na condição nominal de operação do
contactor (a 75 mA) está apresentada na Figura 4.14. Ressalta-se que
a curva foi obtida para a operação do contactor na condição nominal.
Assim, os pontos extremos da curva estão suavizados de forma que a
curva se assemelha a uma elipse. Isso decorre de que, obviamente, na
condição de operação nominal, não ocorre saturação.
Outro detalhe
importante, observado na curva apresentada na Figura 4.14, é que a
inclinação do centro da "elipse" é maior do que a esperada, em relação
ao eixo da indução magnética. Essa condição de inclinação é decorrente
da presença do entreferro de 0,4 mm no contactor. Caso não houvesse
178
Figura 4.13 Forma de onda da tensão CH2 (B) e corrente com baixo
conteúdo harmônico CH1(H).
Fonte: Produção do Autor.
entreferro, a inclinação dos eixos da elipse seria menor.
Essa curva
foi utilizada para o cálculo de perdas de histerese que é exibido na
subsecção 4.4.2.
A Figura 4.15 apresenta a curva de histerese encontrada na condição de saturação. Foram aplicados 260 V na energização do contactor
ao invés dos 220 V da condição nominal.
4.3.5 Curva de saturação magnética BH
Através da curva de histerese obtida experimentalmente (conferir Figuras 4.11 e 4.14), que possui a presença de entreferro, e de
técnicas de interpolação, foi selecionado um material no banco de dados do FEMM, para simulação. E foi incorporado ao mesmo o efeito
do entreferro no material.
Assim, a Figura 4.16 apresenta a comparação das curvas
BH
do material que constitui o contactor, obtida experimentalmente, com
179
Figura 4.14 Curva de histerese do material para a corrente nominal
(75mA), sua acentuada inclinação se deve a presença de um minúsculo
entreferro de 0,4mm, na trave central.
Fonte: produção do autor
a curva obtida pelo material Carpenter, presente no banco de dados
do FEMM, com o efeito de entreferro, que foi desenvolvido para a
simulação por elementos nitos. O material Carpenter foi o que mais
se aproximou do comportamento experimental.
4.3.6 Curva da permeabilidade magnética relativa µr em função da intensidade de campo
A permeabilidade magnética diferencial
diferenciação ponto a ponto dos dados
BH .
B
e
H
µ
se obtém através da
da curva de saturação
Na Figura 4.17 é apresentada a curva de permeabilidade com en-
treferro de 0,4mm. Embora no gráco de saturação magnética
BH ,
a
dispersão de valores sobre a curva de tendência seja mínima, na curva
180
Figura 4.15 Curva experimental de Histerese do material utilizado no
núcleo, sua acentuada inclinação se deve a presença de um minúsculo
entreferro de 0,4mm, na trave central, da mesma forma que na operação
nominal.
Fonte: Produção do Autor.
181
Figura 4.16 Em azul, a curva
BH
do modelo de simulação do mate-
rial Carpenter com o efeito do entreferro e, em vermelho, a curva do
material obtido experimentalmente.
Fonte: Produção do Autor.
de permeabilidade
∆B/∆H ,
variações mínimas produzem uma grande
dispersão de valores. Nestes casos, trabalhou-se com a curva de tendência.
Por praticidade, trabalha-se com a permeabilidade relativa. Assim, na Figura 4.17, os valores foram calculados dividindo a permeabilidade absoluta obtida no processo de diferenciação pela permeabilidade
do ar
µ0 = 4π · 10− 7[ Wb/Am].
4.3.7 Obtenção gráca da permeabilidade absoluta no ponto
de operação para a condição entreferro 0,4mm
Com a acorrente nominal
Inpk = 75 mA, a partir da Figura 4.14,
3000[ A/m]. Utilizando-se com este
obtém-se a intensidade de campo de
valor na curva de permeabilidade relativa, apresentada na Figura 4.17, e
182
Figura 4.17 Gráco da permeabilidade relativa em função da intensidade de campo.
Fonte: Produção do Autor.
multiplicando pela permeabilidade do ar
µ0 , obtém-se a permeabilidade
absoluta neste ponto de trabalho.
Assim, a permeabilidade relativa, a partir do gráco, corresponde
ao valor de
µr = 175.
De modo que a permeabilidade absoluta calculada
é:
µabs = µ0 µr = 2192 · 10−7 [ Wb/Am]
4.3.8 Determinação da Relutância do Contactor
Em forma análoga aos procedimentos do Capítulo 3, a partir
dos pontos obtidos na curva
BH ,
e através da denição da Relutância,
obteve-se a curva de relutância em função da intensidade de campo
H,
este procedimento será realizado para os entreferros de 0,4 mm e 5,0
mm.
Estes valores foram comparados aos obtidos com cálculo clássico
através da simulação, vericando-se o método gráco é uma ferramenta
útil para o cálculo de relutâncias variáveis.
183
A expressão para relutância depende do comprimento médio, da
permeabilidade absoluta e a seção transversal do material, relacionado
isto através da equação constitutiva:
<=
lm
µS
(4.3)
Na Figura 4.18(a), identicam-se os parâmetros geométricos do
contactor e, na Figura 4.18(b), o circuito elétrico equivalente simplicado (desprezando o efeito da espira de sombra e do entreferro de 0,4
mm da trave central do núcleo). Trabalhando com estas ideias, obtevese uma curva de relutância para diferentes condições de entreferros,
apresentada na Figura 4.19.
Figura 4.18 Representação do contactor fechado e do circuito elétrico
simplicado equivalente.
(a) Contactor fechado com entreferro de (b) Circuito elétrico simplicado equiva0,4mm.
lente das relutâncias (são desprezados os
efeitos da espira de sombra e do entreferro
da trave central)
Fonte: Produção do Autor.
Considera-se o comprimento do material magnético lm
= 0, 1156 m,
0, 4 mm, medidas da coluna: 8 · 12 µm2 , me2
considerando espriamento: 12, 2 · 6, 2 µm , fator de
comprimento do entreferro
didas do núcleo
laminação:
0, 9.
Outro aspecto a ser considerado nos cálculos em circuitos magnéticos é que normalmente os núcleos são laminados, como forma de
redução das correntes parasitas. Então, a espessura do isolamento que
separa cada par de lâminas deve ser descontada no cálculo da área;
em outras palavras, a área efetivamente disponível para o uxo (Sf ) é
menor que a área total do núcleo (S ). Assim o fator de empilhamento
é denido como:
f = Sf /S
e, neste caso, se considera 0,9.
184
Figura 4.19 Gráco de relutância do material e em função de entreferros.
Fonte: Produção do Autor.
Assim, para
<t,0,4 =
e para
g = 0, 4 mm
1
1
(<c1 + Rn ) =
2
2
1065, 25
+ 4, 210 · 106
µr
g = 5 mm
<t,5
1
1
= (<c1 + Rn ) =
2
2
1065, 25
+ 64, 59 · 106
µr
185
Ao comparar as expressões se percebe que a relutância no caso
5 mm só acrescenta um fator
5 mm, corresponde a uma
32, 3 · 106 [Am/Wb].
do entreferro de
aditivo, que, neste caso,
para a posição de
relutância constante de
Da Figura 4.19, da relutância em função da intensidade de campo,
se obtém a relutância para o ponto de trabalho especíco do dispositivo.
A intensidade de campo correspondente à corrente nominal Inpk =
75mA é de 3000 [Ae/m], que por sua vez corresponde a uma relutân6
cia < = 5, 3 · 10 [Ae/Wb]. Comparando este valor através do cálculo
realizado via equações de eletromagnetismo clássicas, temos:
<t =
1
2
lm
l0
+
µr µ0 Smn 0, 9 µ0 Smn
Através da simulação numérica no
= 5, 2 · 106 Ae/Wb.
software
FEMM é possível
calcular a relutância a partir do uxo e da força magnetomotriz, assim:
<t =
2 · 5000 · 0, 075
2F
=
= 5, 0 · 106 .
φ
150 · 10−6
A Tabela 4.3 apresenta uma comparação dos resultados de relutância obtidos para o ponto de operação do contactor.
Tabela 4.3 Comparação dos resultados de relutância, com entreferro
de
0, 4 mm.
Método de Cálculo
Gráco
Analítico
Numérico
Valor
Erro
6
5, 3 · 10
5, 2 · 106
5, 0 · 106
4,35%
3,8%
0 % (valor de referência)
O mesmo procedimento apresentado anteriormente pode ser aplicado ao caso do entreferro de
5 mm.
Dessa forma, a Tabela 4.4 apre-
senta os resultados do cálculo de relutância e os respectivos erros, para
o caso do entreferro de
5 mm.
No caso da obtenção gráca da relutância, os valores obtidos,
através de dados experimentais para as duas condições de entreferros,
mostraram que o método gráco é razoavelmente preciso, para entreferros pequenos. Nos maiores, por efeito do espalhamento, o erro aumenta.
Para a obtenção da relutância associada a qualquer entreferro
basta somar a relutância do material com o cálculo no entreferro de
interesse (fator aditivo).
186
Tabela 4.4 Comparação dos resultados de relutância, com entreferro
de
5 mm.
Método de Cálculo
Valor
Erro
Gráco
32, 3 · 106
35, 4 · 106
36, 31 · 106
2,5%
Analítico
Numérico
11%
0% (valor de referência)
4.3.9 Determinação da Curva de Permeância
A Permeância
pm
se dene como o inverso da Relutância (1/<).
Essa propriedade indica a facilidade da passagem de uxo pelo circuito
magnético, equivalente à condutância no circuito elétrico.
Assim:
pm = µ
A
[Wb/A].
lm
(4.4)
A partir de 4.4, facilmente percebe-se que a permeância é proporcional à permeabilidade magnética absoluta.
A Figura 4.20 apresenta a curva de permeância experimental do
contactor.
Através das curvas levantadas e da geometria do dispositivo é
possível realizar qualquer cálculo eletromagnético em forma gráca com
uma precisão na maioria dos casos em torno dos 5%.
4.4 SIMULAÇÕES DO DISPOSITIVO UTILIZANDO A CURVA
BH EXPERIEMENTAL
Uma vez caracterizado o núcleo, é possível inserir estas características no
BH
software
de elementos nitos FEMM. Através da curva
obtida e a corrente de operação é possível realizar as simulações
do material especíco do dispositivo.
Assim, o ponto de operação é
determinado por:
√
2V
2 · 220
=
= 1, 1 [T].
=
N Sω
5000 · 12 · 12 · 10−6 · 2π · 60
√
Bm
A partir da curva
BH
do material, apresentada na Figura 4.16,
determina-se que a intensidade de campo magnético equivalente a
é
H = 3075 [Ae/m].
1, 1 [T]
187
Figura 4.20 Curva aproximada da permeância experimental do contactor.
Fonte: Produção do Autor.
Utilizando a Lei de Ampere:
Hlm = N I → I =
3075 [Ae/m] · 0, 116 [m]
= 0, 071 [A].
5000 [e]
No ensaio, o valor do pico de corrente foi
I = 0, 075 [A].
4.4.1 Determinação da corrente na espira de sombra
Utilizando a curva
BH
experimental e a corrente calculada, o
modelo pode ser testado, neste caso, avaliando a corrente induzida na
espira de sombra (observar Figura 4.21).
Na Figura 4.21, tem-se a representação do vetor de uxo, o qual
pela lei de Faraday induz uma corrente na espira de sombra gerando
um campo magnético que tende a manter fechado o contactor.
O programa fornece como corrente na espira
j13, 47 [A].
I = −31, 28 +
Esse valor complexo representa o defasamento da corrente
na espira em relação à excitação principal. Em módulo, a corrente na
espira
I = 34 [A].
Ressalta-se que o resultado obtido experimental-
188
Figura 4.21 Linhas de uxo
(a) Imagem das linhas magnéticas equi- (b) Imagem das linhas de uxo magnépotenciais do contactor fechado.
tico, o sentido do núcleo está em oposição
com as das colunas.
Fonte: Produção do Autor.
mente foi igual a
37 [A].
O erro percentual foi de 8%. Uma possível
fonte de erro neste caso pode ser o aumento da temperatura pelo efeito
Joule
4.4.2 Determinação da energia dissipada no ciclo de histerese
A energia no ciclo de histerese é dada por:
1
W =
2
Z Z
Bsat
H dBdv,
v
que corrensponde ao produto da área da curva
dispositivo analisado.
Com o auxílio do
software
(4.5)
−Bsat
BH
pelo volume do
Excel, é possível obter o valor da área
BH experimental, apresentada na Figura 4.14. Considerando
3
o volume v = 17, 75 [cm ], a densidade de uxo B = 0, 9 [T] e o campo
magnético H = 1000 [A/m], tem-se que a energia W = 32 [mJ]. Assim,
3
o valor do produto BH obtido é de aproximadamente 3600 [WbA/m ].
Esses valores de B e H utilizados, foram obtidos da aproximação da
curva BH de forma geométrica elipsoidal por um paralelogramo.
da curva
189
A partir da simulação, considerando os dados de corrente e o
núcleo caracterizado, a energia obtida no ciclo de histerese é de
33 [mJ],
este valor será usado como referência para os cálculos de erros.
A diferença de valores da simulação experimental é de
1 [mJ]
(3%).
4.4.3 Perdas no dispositivo
A potência média dissipada no ciclo de histerese é obtida a partir
de:
P =
∆W
= W f.
∆t
(4.6)
Assim, experimentalmente, a potência dissipada no ciclo de histerese, considerando frequência de
forneceu o valor de
2, 0 [W]
60 [Hz],
foi de
1, 9 [W].
A simulação
para a potência dissipada.
Com a informação anterior e a densidade média da liga (7900
[kg/m3 ])
é possível obter as perdas por unidade de volume e massa. Considerando a massa do contactor
0, 140 [kg], a Tabela 4.5 apresenta as perdas
por volume e massa, para diferentes congurações de entreferro.
Tabela 4.5 Perdas por massa e volume para diferentes condições de
entreferro
Entreferro
Perdas por volume
0 mm
0,4 mm
[kW/m3 ]
Perdas por massa
30
3,6
113
14,28
[W/kg]
A discrepância observada entre os valores da literatura (conferir
Tabela 3.6) e os obtidos é explicada pela diferente condição da obtenção
dos dados (frequência, indução magnética e entreferro). Isso é percebido claramente com o aumento do entreferro, que aumenta também
quantidade de perdas por unidade de massa.
4.4.4 Análise energética do contactor a partir da curva BH
A densidade de energia presente no ciclo da curva de magnetização
w
produto
corresponde a diferença da densidade de energia obtida pelo
Hsat Bsat
e da densidade de coenergia, assim, a densidade de
energia é dada por:
190
Hsat
Z
B dH [J/m3 ].
w = Hsat Bsat −
(4.7)
0
Os termos
Hsat
e
Bsat
correspondem respectivamente à inten-
sidade de campo magnético na saturação e a densidade de campo na
saturação. Observar que estes pontos são de difícil denição.
A coenergia é representada pela integração da indução magnética
em função do campo magnético, avaliada da origem até o ponto de
saturação do campo (observar Figura 4.22) e no volume. No caso de
um dispositivo feito de material linear, a energia e a co-energia são
numericamente iguais, o que simplica os cálculo.
Neste caso, esse
princípio não é válido, por se tratar de um material não linear.
O
conceito de "co-energia", embora seja um artifício matemático, facilita
a análise do sistema e permite calcular a força diretamente como uma
função da corrente.
Figura 4.22 Gráco da curva
λi,
regiões de energia e coenergia.
Fonte: adaptado de (CULLITY; GRAHAM, 2009)
Através da curva da saturação magnética da curva
BH ,
obtida
experimentalmente, e com o uso de métodos grácos, é possível obter a
área correspondente a coenergia, descontando da área total é possível
obter a energia no ciclo. Nesta condição, é calculada a potência máxima
disponível.
A densidade de energia para a condição máxima pode ser calcu-
Hsat = 5367 [A/m]
Bsat = 1, 45 [T], tem-se que a densidade energia total é de 7782 [J/m3 ].
3
A densidade de coenergia no mesmo ponto é 4867 [J/m ] (o que resulta
lada de acordo com a Equação (4.7). Considerando
e
191
na coenergia de
51, 74 [mJ],
86, 4 [mJ]).
Assim, a energia máxima de um ciclo é
considerando o volume do dispositivo. Entretanto, devido
à existência do ciclo negativo, a energia total é dobrada, de modo que
Wtot = 103, 5 [mJ].
Utilizando a Equação (4.6), tem-se que a potência máxima do
6, 2 [W]. A partir disso, a potência máxima por unidade
350 [kW/m3 ] e a potência máxima por unidade de massa
é 44, 2 [W/kg].
Para uma corrente de operação de 0, 075 [A] obtida do gráco
BH , está atrelada a intensidade de campo H de 2929 [A/m] e a indução
magnética B de 1, 095 [T], nestas condições a densidade de energia na
3
curva BH é de 3207 [J/m ].
dispositivo é de
de volume é
Utilizando-se o método dos trapézios, é possível calcular a densidade de coenergia e, consequentemente, a energia do dispositivo, na
1772 [J/m3]
50.8 [mJ], o que
condição nominal. Assim, a densidade de coenergia é igual a
e a energia na condição nominal (usando (4.7)) é igual a
representa um erro de
4, 3%
em relação ao valor obtido anteriormente.
A partir da simulação, foi obtido o valor de
48, 7 [mJ]
para a
energia total fornecida, obtido da soma das parcelas de energia em
cada região do sistema (apresentadas na Tabela 4.6).
Tabela 4.6 Distribuição da energia nas regiões do sistema, obtidas
por simulação, para entreferro de 0,4 mm.
Região
Entreferro de
Energia
0, 4 [mm]
[mJ]
29
Perdas do ferro
3,1
Núcleo magnético
1,7
Dispersão no espaço
14,44
Bobina
0,46
Energia total
48,7
Energia da parcela do entreferro é a que pode ser utilizada para
realizar trabalho mecânico
Wg = 29 [mJ],
e, neste caso, corresponde a
energia acumulada na mola.
A diferença entre a energia obtida pela simulação e a curva
BH
se
deve as considerações construtivas, fator de laminação (0,9), espessura
das lâminas (0,5 mm) e condutividade do material ferromagnético, que
consta na biblioteca do FEMM, (4 MS/m). Alterando-se estes parâmetros, a soma se aproxima ou se afasta dos
50 [mJ]
obtidos pelo método
gráco. Alterando estes parâmetros foi possível obter uma energia em
192
torno
49, 5 [mJ],
considerando a hipótese que esta seja uma máquina
otimizada. O erro do método gráco foi de 4%, em relação à simulação
numérica. Com o uso de (4.6), verica-se que a potência nominal é de
3, 48 [W].
5 [mm]
A curva para entreferro de
foi determinada através de
simulações a partir do material Carpenter Silicon Iron.
Para a condição de entreferro de 5 [mm], a corrente obtida foi de
353 [mA] , a intensidade de campo 15354 [A/m] e a indução de 0, 33 [T].
Com isso, ao utilizar-se o método gráco, a energia máxima que pode
ser obtida nesse ponto de operação é igual a
90 [mJ].
Através da simulação por elementos nitos, a energia máxima
desse ponto de operação foi determinada em
84, 6 [mJ].
A Tabela 4.7
apresenta a energia nas diversas regiões simuladas do sistema.
Tabela 4.7 Distribuição da energia nas regiões do sistema, obtidas
por simulação, para entreferro de 5 mm.
Região
Entreferro de
Energia
5 [mm]
Perdas do ferro
[mJ]
44,6
0.57
Núcleo magnético
0,1
Dispersão no espaço
30.53
Bobina
8,8
Energia total
84,6
Para manter a mesma indução ocorre um aumento na corrente
que vai dos 53 [mA] aos 250 [mA], isto é, um aumento de 5,4 vezes a
corrente de operação.
4.4.5 Triângulo de potência
Da curva BH anterior, é possível, através dos conceitos de energia
e coenergia, encontrar a máxima energia que o dispositivo pode fornecer. Com isso, encontra-se a potência ativa máxima. Como a corrente
e a tensão nominais são conhecidas, facilmente se obtém a potência
aparente do dispositivo.
Através de relações trigonométricas, obtém-se a potência reativa
e fator de potência ótimo para a operação do dispositivo. Neste cálculo,
não foi levada em consideração o efeito das harmônicas na corrente.
Da seção anterior, através do gráco se obteve para a condição
de corrente nominal (Inpk
= 75 [mA]) uma energia de 51 mJ que corres-
193
ponde a uma potência de ativa de 3,1 W. Como é conhecida a corrente
e tensão nominal , facilmente se obtém a potência aparente. Através de
relações trigonométricas, se obtém a potência reativa e fator de potência ótimo para a operação do dispositivo. Neste cálculo não foi levada
em consideração o efeito das harmônicas na corrente.
Dessa forma,
a Tabela 4.8 sintetiza os valores teóricos e experimentais de potência
obtidos no contactor.
P = 51 [mJ] · 60 [Hz] = 3, 2 [W];
S = 220 [V] · 53 [mA] = 11, 66 [VA];
p
Q = 11, 662 − 3, 12 = 10, 9 [VAr ];
Tabela 4.8 Triângulo de potência do contactor.
Tipo de potência
Resultado teórico
Resultado experimental
3, 1 [W]
11, 24 [VAr ]
11, 66 [VA]
71◦
3, 2 [W]
10, 9 [VAr ]
11, 66 [VA]
73◦
Ativa
Reativa
Aparente
Ângulo
Utilizando a curva de saturação
BH ,
é possível determinar a
energia máxima, (produto da área máxima multiplicada pelo volume),
para se obter a potência máxima por ciclo de rede deve-se multiplicar
a energia máxima pela frequência, com isto tem-se a potência máxima
ativa que o dispositivo pode fornecer.
Utilizando a mesma metodologia foram feitos cálculos para a
potência ativa nominal utilizando a corrente de operação, no caso especíco, para 75 [mA] corrente de pico.
Como é conhecida a tensão
para esta corrente é possível facilmente obter a Potência Aparente e
em função do triângulo de potências a Potência Reativa e o Fator de
Potência do dispositivo.
A curva
BH
obtida experimentalmente também ajuda a identi-
car os tipos de materiais utilizados pelos fabricantes nos dispositivos.
194
4.4.6 Energia e força nos entreferros
O cálculo de energia e força nos entreferros será realizado através
de quatro métodos descritos a seguir:
ˆ
método gráco pela curva BH, especíca para cada entreferro;
ˆ
método da energia no entreferro;
ˆ
método da densidade de força;
ˆ
método de elementos nitos.
Considerando a energia acumulada no volume do entreferro do
contactor:
Z
0
w =
uma vez que, no entreferro,
w0 =
B0 dH,
B0 = µ0 H0 ,
Z
µ0 H0 dH =
(4.8)
temos que
1
B2
µ0 H02 = 0 .
2
2µ0
(4.9)
Para encontrar a energia no entreferro, é necessário calcular todo
o volume do entreferro, considerando o efeito do espalhamento na secção
transversal (observar Figura 4.23). Assim, a energia é dada por
W0 =
em que
S0
B02 0
S g,
2µ0
é a seção transversal corrigida e
(4.10)
g
é o comprimento do en-
treferro. Essa equação evidencia o fato que a energia no entreferro é
proporcional ao quadrado da indução.
Através da curva de saturação magnética
BH
para entreferros
especícos, obtém-se os valores da indução, tornando possível calcular
a energia no entreferro e, consequentemente, a força.
Será utilizado o método gráco para o cálculo de energia em duas
condições de entreferros de
0, 4
e
5 [mm].
A força é dada por:
Fc =
W0
,
g
(4.11)
No caso da operação CC, dessa forma,
Fc =
B2 0
S.
2µ0
(4.12)
195
Figura 4.23 Entreferro e espalhamento associado.
Fonte: adaptado de (NOGUEIRA; BOUDEC, 2007)
No caso da operação CA, supondo que a corrente e o uxo sejam
perfeitamente senoidais, temos que:
B = Bmax cos(ωt).
(4.13)
Substituindo (4.13) em 4.12, temos que:
Fc =
2
Bmax
cos2 (ωt) 0
S.
2µ0
(4.14)
Com o uso da identidade trigonométrica
cos2 (ωt) =
1 1
+ cos(2ωt),
2 2
(4.15)
tem-se que a força CA é dada por:
FCA =
Para
ω = 0,
2
Bmax
B 2 cos(2ωt) 0
S 0 + max
S.
4µ0
4µ0
(4.16)
a força CC é:
FCC =
2
Bmax
B2
S 0 + max S 0 = 2FCA,med
4µ0
4µ0
(4.17)
196
A Figura 4.24 auxilia na compreensão da força CA, através da
exibição da forma de onda no tempo.
Figura 4.24 Formas de onda da corrente e força no contactor, a força
tem dobro da frequência da corrente.
Fonte: produção do autor
4.4.6.1 Método gráco através da curva BH da energia acumulada no entreferro de 0, 4 mm
0, 4 [mm] do gráco BH com a
= 75 [mA]), obtém-se a intensidade de campo
H = 3000 [A/m]), e a indução B = 1.095 [T] no entreferro. O uxo pode
2
ser obtido pelo produto da indução e da seção transversal (144 [µm ]).
Assim, o uxo no núcleo φ = 157 [µWb]. Na simulação, obteve-se
B = 0, 08 [T] e φ = 153 [µWb], com erros do método gráco de 8% e
Para a condição de entreferro de
corrente de operação (i0
3% respectivamente.
Utilizando (4.10), tem-se que a energia no entreferro é
W0 =
1, 12
(12 + 0, 2)2 (0, 4) · 10−9 = 29 [mJ].
2µ0
Observar que as dimensões do núcleo foram acrescentadas em
g/2
0, 4/2mm.
0, 4 [mm], F = 72, 5 N.
por causa do espalhamento do uxo, neste caso,
Com o uso de (4.11), para o entreferro de
197
4.4.6.2 Método gráco através da curva BH da energia acumulada no entreferro de 5 mm
No caso da presença de entreferros variáveis, é possível conseguir
a curva BH por simulação a partir da curva obtida experimentalmente.
A metodologia, neste caso, é denir o material com a curva BH experimental, criar o entreferro no qual o dispositivo vai operar e através
de um programa implementado em LUA (conferir Anexo F) obter as
características BH para os diferentes valores de correntes.
Experimentalmente se encontrou uma corrente de
caz (353
[mA]
de pico) para o entreferro de
5 [mm].
250 [mA]
e-
No Figura 4.25,
desenvolvido pela simulação, se localizam estes valores.
Figura 4.25 Gráco da curva de saturação magnética BH do mesmo
material anterior com um entreferro de 5mm, é possível perceber que
em função deste grande entreferro a curva se torna linear.
Fonte: Produção do Autor.
A partir de (4.10) e dos dados da curva
5 [mm],
BH
com entreferro de
obtidos por extrapolação, calcula-se a energia nos entreferros
198
46 [mJ],
48 [µWb].
de
para a corrente de pico de
O valor de
pico de
350 [mA],
B
350 [mA], B = 0, 333 [T]
e
φ=
considerado foi obtido, considerando a corrente de
tem-se que:
H=
N
5000
· 0, 350 = 15354 [A/m].
Ie =
lm
0, 116
Associando o valor de
H
O valor da energia
com a Figura 4.25, se obtém
W
B = 0, 333 [T].
foi obtido considerando:
B2
0, 3332
· (12 + 2, 5)2 · 5 · 10−9 = 46 [mJ].
v=
2µ0
2 · 4π · 10−7
W =
Observar que as dimensões do núcleo foram acrescentadas em
g/2
0, 4/2mm.
FCC = 4, 6 [N] envalor CC, logo FCA =
por causa do espalhamento do uxo, neste caso,
Utilizando (4.11), a força de atração CC é
quanto a força de atração CA é a metade do
2, 3 [N].
4.4.6.3 Método das energias nos entreferros
A energia nos entreferros será calculada através do Tensor de
Maxwell, a indução
B
necessária para realizar os cálculos será obtida
por simulação.
No caso do contactor aberto, existem 2 entreferros, as colunas e
o núcleo (trave central), do núcleo e as colunas (simétricos).
Da simulação, encontra-se que
rando o volume
v
B = 0, 149 [T],
assim, conside-
do material magnético, a energia acumulada no en-
treferro da coluna é dada por:
Wc =
B2
0, 1492
v=
· (8 + 2, 5)2 · 5 · 10−9 = 6, 7 [mJ].
2µ0
2 · 4π · 10−7
Observar que as dimensões do núcleo foram acrescentadas em
0, 4/2mm.
B = 0, 273 [T], assim,
g/2
por
causa do espalhamento do uxo, neste caso,
Da simulação, encontra-se que
a energia
acumulada no núcleo é dada por:
Wn =
0, 2732
B2
v=
· (12 + 2, 5)2 · 5 · 10−9 = 31, 2 [mJ].
2µ0
2 · 4π · 10−7
199
Assim, o total de energia obtida é:
Wte = Wc + Wn = 2 · 6, 7 + 31, 2 = 44, 6 [mJ].
A Tabela 4.9 sintetiza os resultados obtidos no cálculo das energias.
Tabela 4.9 Energia acumulada no contactor.
W 0 [mJ]
Região
B [T]
φ [µWb]
Entreferro das colunas
0,149
14,3
6,7
Entreferro do núcleo
0,273
39,3
31,2
Com os dados da Tabela 4.9, conclui-se que a energia total é de
44, 6 [mJ].
Com isso,
Fc =
44, 6 [mJ]
= 4, 46 [N].
2 · 5 [mm]
A Figura 4.26 apresenta o espalhamento do uxo magnético, na
simulação desenvolvida para o cálculo da força pelo método da energia.
Figura 4.26 Espalhamento do uxo magnético no entreferro e energia
acumulada.
Fonte: Produção do Autor.
Com a Figura 4.26, é possível perceber os problemas da obtenção da indução magnética média, já que esta varia ao longo do percurso
traçado. Por outro lado tem-se a elevada dispersão de uxo que caracteriza entreferros grandes.
200
4.4.6.4 Método da densidade de força (pressão magnética)
Este método utiliza o conceito da pressão magnética e será descrito a partir da equação do tensor de Maxwell. Considerando as Equações (4.10) e (4.11), temos que
Fc =
em que
B = µ0 N i/g , g = 2x
e
B2 0
S,
2µ0
µ0 = 4π · 10−7 [H/m].
Fc =
Assim,
µ0 2 2 0
N i S.
8x2
Dividindo (4.19) pela área corrigida
força ou pressão magnética
(4.18)
(4.19)
S0,
obtém-se a densidade de
pm , nessas duas regiões que separam os dois
pares de faces polares. Assim,
pmag =
µ0 2 2
N i .
8x2
(4.20)
Conforme a Figura 4.27, para o caso particular do dispositivo
em estudo, temos
pmag =
x = 5 [mm], N = 5000 [e]
e
i = 250 [mArms ].
Logo:
4π · 10−7 · 50002 · 2502 · 10−6
= 9812, 5 [N/m2 ]
8 · 52 · 10− 6
Para o cálculo da força é preciso multiplicar a pressão magnética
pmag
pela área das interfaces ferro-ar nas duas traves laterais e trave
central do acionador, no caso
A força magnética
FCC
S 0 = 5148 [µm2 ].
na operação em corrente contínua é:
FCC = pmag S 0 = 5, 05 [N].
A força CA, conforme (4.17), é
FCA = 2, 525 [N].
4.4.6.5 Método dos elementos nitos
Utilizando a curva BH experimental e os dados geométricos do
entreferro, simulou-se a operação do contactor. Dessa maneira, a força
foi obtida de forma direta com o auxílio do vetor ponderado de Maxwell.
A Tabela 4.10 sintetiza os resultados obtidos.
201
Figura 4.27 Contorno para o cálculo do campo.
Fonte: adaptado de (NOGUEIRA; BOUDEC, 2007)
Tabela 4.10 Síntese dos resultados obtidos com o Tensor Ponderado
de Maxwell.
Tipo de Força
Componente
x [N]
Componente
CC
-0,0147
-5,45
CA
-0,0073
-2,73
y [N]
4.4.6.6 Comparação dos métodos de cálculo de força
A partir dos resultados apresentados na seção anterior, é possível
realizar o compartivo dos métodos de cálculo de força apresentados:
ˆ
Método da curva
BH
Requisitos: dispor do gráco BH, com escalas apropriadas
ou das tabelas que o geraram.
Para
ω = 0, FCC = 4, 6 [N].
Para
ω 6= 0, FCA = 2, 3 [N].
Erro em relação à simulação: 15%.
202
ˆ
Método das energias nos entreferros
Requisitos: conhecer a geometria dos entreferros e a indução
magnética B na região de interesse.
ˆ
Para
ω = 0, FCC = 4, 46 [N].
Para
ω 6= 0, FCA = 2, 23 [N].
Erro em relação à simulação: 18%.
Método da densidade de força (pressão magnética)
Requisitos: conhecer geometria dos entreferros e dados construtivos do dispositivo.
ˆ
Para
ω = 0, FCC = 5, 05 [N].
Para
ω 6= 0, FCA = 2, 525 [N].
Erro em relação à simulação: 7%.
Método dos elementos nitos
Requisitos: conhecer a geometria do dispositivo e a curva de
saturação magnética BH do material.
Para
ω = 0, FCC = 5, 45 [N].
Para
ω 6= 0, FCA = 2, 72 [N].
Esses resultados foram utilizados como referência.
A Figura 4.28 apresenta um estudo comparativo das forças através de elementos nitos de um contactor operando em corrente CC, CA
e pelo tensor de Maxwell. Observar que, através da Figura 4.28, não
é possível armar que a força CC é o dobro da força CA para toda a
distância, mas apenas para pequenas condições de entreferro.
Em todos os casos o valor de pico da corrente foi considerada de
250 [mA]
e o comprimento do entreferro variando de 1 até
5 [mm].
Ao
representar gracamente a força em função do entreferro percebe-se que
para entreferros maiores que 10% das grandezas geométricas envolvidas
não é possível armar experimentalmente que a relação
seja válida. Para um entreferro de
2 [mm],
FCC = 2 · FCA
só é possível armar que a
força CC é levemente maior que a CA.
Através do tensor de Maxwell é possível perceber que a força varia com o valor inverso do quadrado da distância do entreferro, gerando
um formato típico de uma equação quadrática.
Para a simulação do tensor de Maxwell em função do entreferro
utilizou-se a expressão:
203
Figura 4.28 Força produzida no contactor por uma corrente alternada
(azul) e por uma contínua (vermelha) com um entreferro variando de
zero até 5mm. Em verde, o tensor ponderado.
Fonte: Produção do Autor.
Fc =
onde
Kcont = 51, 57 [Nmm2 ]
µ0 2 2 0
Kcont
N i S =
,
8x
x2
e
(4.21)
x ∈ (0, 5] [mm].
Os métodos propostos para a obtenção da energia e da força nos
entreferros apresentam bons resultados considerando a elevada dispersão que o entreferro de
5 [mm] introduz, o que contribui em muito para
os erros.
O método através da curva de saturação magnética
BH ,
em-
bora apresente um erro de 15%, resulta de interesse pela simplicidade
e rapidez.
A partir da curva de material levantada experimentalmente, é
possível obter uma curva de saturação magnética
BH
para uma con-
dição de entreferro especíca.
Ao trabalhar a expressão da força em CA conclui-se que força
em CC é o dobro da CA, percebível só com entreferros 10% menores
204
que as grandezas envolvidas, e a frequência da força resulta ser o dobro
de frequência fundamental da corrente.
4.5 MODELAGEM ELÉTRICA DO DISPOSITIVO
No modelo de núcleo fornecido pelo FEMM, os componentes de
indutância própria e resistência equivalente das perdas se encontram em
série (Figura 4.29). Entretanto, na literatura de máquinas, usualmente
estes modelos são apresentados como circuitos paralelos (Figura 4.30).
Figura 4.29 Modelo elétrico do contactor no FEMM, a indutância e
o resistor equivalente estão em série.
Fonte: Produção do Autor.
Utilizando as expressões previamente deduzidas e considerando
as perdas na resistência do bobinado como sendo desprezíveis pode ser
feita a mudança de série para paralelo. O modelo paralelo é usualmente
utilizado para a modelagem das perdas em dispositivos eletromagnéticos.
Da simulação do contactor fechado utilizando a curva BH experimental e a corrente nominal, foram obtidos os resultados apresentados
na Tabela 4.11.
A resistência paralela equivalente é dada por:
"
Rp = Rs
Xls
Rs
2
#
+ 1 = 21768 Ω.
205
Figura 4.30 Modelo elétrico do contactor, a indutância e o resistor
equivalente estão em paralelo.
Fonte: Produção do Autor.
Tabela 4.11 Resultados da simulação no FEMM.
Corrente total
0,075 Ampere
Queda de tensão
337 Volt
Fluxo concatenado
0.877304-j 0,15212 Weber
Fluxo por corrente
11,6974-j 2,02827 Henry
Impedância
933,234+j 4409,81 Ohm
Potência ativa
2,62472 Watt
Potência reativa
12,4026 VAr
Potência aparente
12,6773 VA
A reatância paralela equivalente é dada por:
"
Xlp = Xls
Rs
Xls
2
#
+ 1 = 4606 Ω.
Em ambos os casos, deve-se utilizar os fatores de compensação
Rp = 311/337 · 21768 = 20026 [Ω]
Xlp = 311/337 · 4606 = 4238 [Ω], o que resulta em Lp = 11, 24 [H].
Experimentalmente, foram obtidos Rp = 20670 [Ω] e Lp = 10, 45 [H].
comentados na Seção 3.4. Assim,
e
Dessa maneira, os erros obtidos foram de 3% e 7% respectivamente.
206
As perdas no núcleo são dadas pela soma das perdas por histerese
e pelas correntes de Foucault, resultando em 0,5 Watt.
As perdas do cobre são dadas unicamente pelo efeito Joule na
bobina, assim podemos determinar a resistência série equivalente destas
perdas, neste caso, Pcu = 0, 8035 Watt. Assim, como a corrente é de
53 [mA], a resistência se determina pela expressão P = Req I 2 , de modo
que, Req = 286 [Ω].
Experimentalmente, encontrou-se uma resistência para o bobinado de
Req = 534 [Ω].
No procedimento, utilizou-se uma fonte de
corrente CC e para a medição da queda tensão.
O erro é da ordem
dos 46%, de modo que uma causa provável para o mesmo seja a determinação da bitola utilizada na simulação. A Figura 4.31 apresenta
o resultado da simulação desenvolvida para obtenção das perdas no
cobre.
Figura 4.31 Perdas no núcleo.
Fonte: Produção do Autor.
Na bobina, a perda do cobre foi de 0,475 W e nas espiras ao todo
de 0,33W. A perda total do cobre
Pcu
foi de
0, 8 W
e a do ferro
PF e
foi
de 1,82 W. Assim, as perdas totais foram de 2,62 W
Assim, a perda total é dada pela soma das perdas no núcleo, nas
bobinas e nas espiras, o que resulta em
2, 6525 [W].
207
4.6 EFEITOS DO ENTREFERRO NO PROJETO DE DISPOSITIVOS ELETROMAGNÉTICOS
Os efeitos de um pequeno entreferro no núcleo da bobina de um
contactor produzem uma linearização da indução
B,
o que por sua vez
afeta o formato da corrente no acionamento tornado- a mais senoidal,
com isso as harmônicas são reduzidas. Os grácos apresentados são de
um pequeno transformador onde se introduziu um entreferro de aproximadamente
0, 3 [mm]
com o uso de uma ta isolante, resultando na
alteração no formato da onda (o que é observado nas Figuras 4.32 e
4.33).
Figura 4.32 Formato de onda da corrente sem entreferro.
Fonte: Produção do Autor.
As Figuras 4.34 e 4.35 apresentam, respectivamente, o espectro
de frequência da corrente sem a presença de entreferro e com a presença
de entreferro.
Assim, através da análise da taxa de distorção harmônica (THD),
calculada a partir do espectro, observa-se que, sem o entreferro, a distorção na corrente atinge 32,14%. A presença do entreferro, porém, faz
com que a corrente apresente 5,2% de distorção harmônica. Isso mostra
que o uso do entreferro auxilia na melhora da eciência energética do
elemento magnético.
208
Figura 4.33 Formato de onda da corrente com entreferro.
Fonte: Produção do Autor.
Figura 4.34 Espectro da forma de onda da corrente sem entreferro
(THD = 32,14%).
Fonte: Produção do Autor.
209
Figura 4.35 Espectro da forma de onda da corrente com entreferro
(THD = 5,2%).
Fonte: Produção do Autor.
A Figura 4.36 apresenta o esquema de montagem da inserção do
entreferro.
A corrente, ao trabalhar numa região mais linear, reduz suas perdas, é de interesse comparar o desempenho das ligas de ferro ao silício
M-27 e Carpenter com e sem entreferro de
0, 4 [mm].
Os resultados
são apresentados na Tabela 4.12. Nela pode-se comparar, entre outras
grandezas, as perdas do ferro e a corrente na espira de sombra para
cada situação.
Um fato de interesse é que, ao trabalhar-se com um pequeno entreferro, diferentes tipos de material apresentam praticamente o mesmo
desempenho, como é o caso do M-27 e do Carpenter.
Dessa forma,
num âmbito comercial, há interesse para fabricantes de contactores poder adquirir desempenho similar com materiais diferentes, pois evita-se
dependências de fornecedores especícos.
4.7 CONSIDERAÇÕES FINAIS DO CAPÍTULO
O método da transformação de impedâncias atende os modelos
série (FEMM) e paralelos (clássico). Os dados experimentais da carac-
210
Figura 4.36 Montagem de transformador inserindo um entreferro de
0,4mm.
Fonte: produção do autor
terização do núcleo estão próximos aos obtidos pela simulação a partir
da curva BH levantada, sendo que o maior erro está em torno dos 7%.
Existe uma grande discrepância com a resistência da bobina,
atribuído à diculdade de medir a bitola do o.
Ao introduzir um minúsculo entreferro melhora-se o desempenho
do material no dispositivo e reduz-se o conteúdo harmônico.
A técnica do entreferro pequeno permite que materiais com curvas BH diferentes apresentem um mesmo desempenho evitando a dependência de fornecedores especícos.
Com esse estudo, pode-se perceber que, através de um circuito
de baixo custo, é possível obter-se a curva de histerese. Esta curva do
ponto de vista das energias envolvidas correspondente às perdas totais
do núcleo magnético (perdas de histerese+Foucault+anômalas), assim
permite avaliar a eciência energética do dispositivo.
Utilizando os dados experimentais e programas Excel ou Matlab
foi possível traçar a curva BH característica do material ferromagnético
permitindo sua identicação na biblioteca de materiais. Das relações
constitutivas e da geometria do dispositivo podem ser obtidas as curvas
de: Permeabilidade, Indutância e Relutância. Em todos os casos os valores obtidos gracamente foram calculados por métodos alternativos e
211
Tabela 4.12 Resultados da simulação no FEMM.
Grandeza
Física
M-27
(0,4 mm)
M-27
Carpenter
(0,4 mm)
Carpenter
0,071
0,071
0,071
0,071
41,7+j 283,6
116+j 504
39,7+j 284
122+j 516
0.75-j 0,078
1,3-j 0,2
0.75-j 0,07
1,4-j 0,3
10.6-j 1,1
8,9-j 3,9
10.7-j 1.0
19,4-j 4,1
0.6+j 4,0
1,6+j 7,1
0.6+j 4,0
1,7+j 7,3
1,47
4,12
1,41
4,3
10,1
17,8
10,1
18,2
10,2
18,3
10,2
18,7
na
36,8
70,8
35,3
72,3
no
0,198 W
0,652
0,199
1,4
Corrente total [A]
Queda
de
tensão [V]
Fluxo concatenado [Wb]
Fluxo
por
corrente [H]
Impedância
[kΩ ]
Potência
ativa [W]
Potência reativa [VAr]
Potência
aparente
[VA]
Corrente
espira [A]
Perdas
núcleo [W]
nalmente por simulações, estas últimas são utilizadas como referência
na avaliação da precisão obtida. Utilizando as curvas traçadas no cálculo de grandezas especícas a técnica gráca mostra-se rápida e, na
maioria dos casos, precisa.
A curva de relutância para qualquer condição de entreferro pode
ser calculada a partir da curva do material sem entreferro somando um
fator aditivo que corresponde à relutância que apresenta o entreferro,
obtendo assim um conjunto de curvas que permite simplicar o cálculo
de uxo para diferentes condições de entreferro.
A presença de entreferro melhora o desempenho do material no
dispositivo e reduz o conteúdo harmônico. Também observou- se que
materiais com curvas BH diferentes apresentam um mesmo desempenho
evitando a dependência de fornecedores especícos.
212
Ao trabalhar a expressão da força em CA conclui-se que força
em CC é o dobro da CA, percebível em forma experimental só com
entreferros 10% menores que as grandezas envolvidas. A frequência da
força resulta ser o dobro da frequência fundamental da corrente.
Por m, com este estudo de dispositivos com entreferro, percebeuse que as metodologias abordadas também serviriam para avaliar o
desempenho e eciência de máquinas girantes de indução.
213
5 CONSIDERAÇÕES FINAIS
Este trabalho apresenta uma síntese do estado da arte sobre as
caracterizações e perdas no ferro sob o enfoque da Engenharia Elétrica;
teve a intenção de compreender e gerar subsídios para a caracterização de materiais ferromagnéticos aplicado na avaliação de parâmetros
eletromagnéticos e de eciência energética de dispositivos eletromagnéticos utilizando uma técnica simples e de baixo custo, dispensando
instrumentação cara e em alguns casos não disponíveis.
Os resultados obtidos foram satisfatórios do ponto de vista de
uma análise qualitativa dos fenômenos, mostrando coerência entre a
simulação e obtenção dos parâmetros na aplicação do modelo, tanto
para o caso do transformador quanto para o caso do contactor.
No caso dos parâmetros do modelo de Steinmetz do transformador, o erro dos parâmetros obtidos foi aceitável. Da mesma forma, o
erro da corrente de
Inrush
em relação ao resultado experimental foi pe-
queno, demostrando a validade do modelo na previsão desse complexo
fenômeno.
No caso da força no contactor, embora o erro apresentado tenha
sido alto, os resultados obtidos com o modelo garantem uma boa noção
do valor. A vantagem do método qualitativo apresentado é a rapidez
de cálculo e a visão macro do processo, apesar dos erros em relação ao
valor real da força.
Desta forma, é perceptível que a visão qualitativa fornecida pelos
grácos e curvas das características eletromagnéticas dos dispositivos
pode ajudar, do ponto de vista pedagógico, na compreensão do funcionamento e no projeto de máquinas elétricas e transformadores.
O processo de obtenção da caracterização dos materiais através
dos grácos BH permite denir o material e corrente, requisitos básicos
para tornar possível rodar programas simuladores destinados à análise,
concepção e projeto de dispositivos eletromagnéticos (FEMM).
O ponto de partida é a curva de histerese, a qual é obtida através de um circuito RC e de osciloscópio digital, e, a partir desta, com
auxílio de programas como Excel e MatLab, os pontos são tratados
derivando em diferentes grácos como curva BH, permeabilidade diferencial e outros usuais no projeto de máquinas.
E, com o auxílio da
teoria eletromagnética se consegue obter os outros parâmetros de dis-
214
positivos com e sem entreferro.
Por condições inerentes do processo
digital os bancos de dados do material são criados em forma natural.
A caracterização obtida também permite fazer uma abordagem
através dos conceitos de energia e coenergia obtendo assim a potência
máxima, perdas do ferro, eciência energética e o triângulo de potencias do dispositivo. A caracterização das perdas do ferro através das
curvas de histerese a diferentes frequências possibilita a obtenção da
equação Steinmetz Bertotti para a separação das perdas do ferro, em
histerese, excedentes e de Foucault .
Esta equação também permite
avaliar as perdas geradas por correntes não senoidais através de seu
espectro harmônico utilizando a série de Fourier.
A metodologia experimental abordada neste trabalho pode ser
facilmente adaptada ao roteiro de laboratório das disciplinas de Conversão de Energia e Materiais Elétricos do curso de graduação de Eng.
Elétrica levando o aluno a um plano mais prático, agregando motivação
ao estudo de temas complexos e abstratos.
5.1 PUBLICAÇÕES GERADAS AO LONGO DESSE TRABALHO
As seguintes publicações foram geradas ao longo desse trabalho:
ˆ
A.F.L. Nogueira, L.J.A.S. Maldonado and F.C. Schulz. Analytical and nite-element calculation of magnetic forces on
ac contactors [devices], Revista Sodebrás, vol. 8, n. 89, maio,
2013.
The principle of
duality between electric and magnetic circuits applied to
the analysis of electromagnetic devices/ the use of fea to
overcome the limitations of the classical magnetic circuit
analysis, IJRRAS, vol. 1 n. 3, 2013.
ˆ
A. F. L. Nogueira andL.J.A.S. Maldonado.
ˆ
A. F. L. Nogueira andL.J.A.S. Maldonado.
Analysis of ac contactors combining electric circuits, time-harmonic nite
element simulations and experimental work, 2013.
O resumo dessas publicações está incluido no Anexo E.
215
5.2 PERSPECTIVAS DE EVOLUÇÃO DA METODOLOGIA
No desenvolvimento deste trabalho apareceram séries de dúvidas,
as quais poderão servir como ponto de partida de novas investigações,
ou corrigidas e explicadas.
Enumeram-se possíveis trabalhos de continuação:
1. Extensão do estudo para os núcleos de transformadores de ferrite
amplamente utilizados na eletrônica de potência;
2. Aprimorar a metodologia da obtenção das reatâncias dispersivas
que apresentaram erros elevados;
3. Desenvolvimento de uma bancada experimental em função de um
estudo das perdas rotacionais, visando aplicar a metodologia a
motores elétricos;
4. Estudo de procedimentos experimentais para avaliar a eciência
energética de máquinas girantes através dos conceitos de energia
e coenergia;
5. Metodologia para avaliar a condutividade dos materiais ferromagnéticos do ponto de vista do modelo das perdas magnéticas por
corrente induzidas clássicas;
6. Avaliar o tratamento térmico nas chapas de aço 1010 e obter outro
tipo de amostra para testar a metodologia;
7. Banco de dados das curvas obtidas de materiais ferro e Ferri magnéticos;
8. Desenvolver instrumentação para trabalhar em regime quase estático (em torno de 1 Hz);
9. Implementar o algorimmo para obter o modelo de Jiles-Athertom
a partir da curva de Histerese.
216
217
REFERÊNCIAS BIBLIOGRÁFICAS
Caractérisation et Prédiction des Pertes dans les
Tôles Fer Silicium Soumises à des Tensions Non-Sinusoidales.
AMAR, M.
Tese (Doutorado) Université Paris, 1994.
BASTOS, J.
Eletromagnetismo e cálculo de campos.
2nd. ed.
Florianópolis: Ed. da UFSC, 1992.
Caracterização e modelagem eletromagnética de lâminas de aço ao silício. Tese (Doutorado) UFSC, 2001.
BATISTELA, N. J.
BECKER, J. J. Magnetization changes and losses in conducting ferromagnetic materials.
Journal of Applied Physics,
1963. v. 34, n. 4,
p. 13271332, 1963.
BERTOTTI, G. Space-time correlation properties of the magnetization
process and eddy current losses: Theory.
J. Appl. Phys, 1983. v. 54,
n. 9, p. 52935305, 1983.
BERTOTTI, G. Space-time correlation properties of the magnetization
process and eddy current losses: Applications. i. ne wall spacing.
Appl. Phys, 1984. v. 55, n. 12, p. 43394355, 1984.
J.
BERTOTTI, G. Physical interpretation of eddy current losses in ferromagnetic materials. i. theoretical considerations.
J. Appl. Phys, 1985.
v. 57, n. 6, p. 2110 2126, 1985.
BERTOTTI, G. General properties of power losses in soft ferromagnetic
materials.
IEEE Transactions on Magnetics,
1988. v. 24, n. 1, p.
621630, 1988.
BOZORTH, R. M.
Ferromagnetism. 3rd. ed. New Jersey:
John Wiley
& Sons, 2000.
CAMPOS, M. F.; EMURA, M.; LANDGRAF, F. J. Consequences of
Journal of Magnetism and Magnetic Materials, 2006. v. 304, p. 593595, 2006.
magnetic aging for iron losses in electrical steels.
Introdução ao método dos elementos nitos
para engenheiros eletricistas. São Paulo: Editoração Própria, 1995.
CARDOSO, J. R.
218
CULLITY, B. D.; GRAHAM, C. D.
terials. 2nd. ed. New Jersey:
Introduction to Magnetic Ma-
IEEE Press, 2009.
DECRISTOFARO, N. Amorphous metals in electrical-power distribution applications.
Materials Research Society Bulletin, 1998. v. 23,
p. 5056, 1998.
Electrical Machines.
DRAPER, A.
London: Longmans, Green and
Co Ltd, 1963.
Measurement and Characterization of Magnetic
Materials. 1st. ed. [S.l.]: Elsevier, 2004.
FIORILLO, F.
FIORILLO, F.; NOVIKOV, A. Power losses under sinusoidal, trapezoidal and distorted induction waveform.
IEEE Trans. Magn., 1990.
v. 26, n. 5, p. 2559 2561, 1990.
FISH, G. E. Soft magnetic materials.
Proceedings of IEEE,
1990.
v. 78, n. 6, p. 947971, 1990.
FRAME, J. R.; MOHAN, N.; LIU, T. Modeling in an electromagnetic
transients program theory. IEEE Transactions on Power Apparatus and Systems, 1982. v. 101, n. 9, p. 34033412, 1982.
Subdivisão das perdas histeréticas em aços
elétricos deformados e recozidos. 2010.
FUKUHARA, M.
FÜZI, J. Computationally ecient rate dependent hysteresis model.
The International Journal for Computation and Mathematics
in Electrical and Electronic Engineering, 1999. v. 18, n. 3, p.
445457, 1999.
Análise de perdas em sistemas
de energia que empregam materiais supercondutores de alta
temperatura. Tese (Doutorado) Universidade de Porto, 2010.
GONÇALVES-MONTEIRO, A.
GRAHAM, J. C. Physical origin of losses in conducting ferromagnetic
materials.
Journal of Applied Physics,
1982. v. 53, n. 11, p. 8276
8280, 1982.
GRAY, C. B.
Electrical Machines and Drive Systems. New York:
John Wiley & Son, Inc., 1989.
GROSSNER, N.
Transformers for Electronic Circuits.
New York: McGraw-Hill Book Company, 1983.
2nd. ed.
219
Correntes transitorias de magnetizacao
em transformadores de potencia. 2010.
GUERRA, F. das C. F.
HAMDI, E. S.; NOGUEIRA, A.; SILVESTER, P. P. Torque compu-
IEE Proceedings-Pt. A
Science, Measurement and Technology, 1993. v. 140, n. 2, p.
tation by mean and dierence potentials.
151154, March 1993.
HAMMOND, P.
Applied Electromagnetism. Great Britain:
Perga-
mon Press, 1971.
Electromagnetism for Engineers - an introductory course. 3rd. ed. Great Britain: Pergamon Press, 1986.
HAMMOND, P.
HOLLITSCHER, H. Core losses in magnetic materials at very high
IEEE Transactions on
Magnetics, 1969. v. 5, n. 3, p. 642646, 1969.
ux densities when the ux is not sinusoidal.
INFOLYTICA. Announcement #35: Loss calculation in transient solvers available in latest version of MagNet. 2006. Disponível em: <http://www.infolytica.com>.
JILES, D. C.; ATHERTON, D. L. Theory of ferromagnetic hysteresis.
Journal of Magnetic Materials, 1986. v. 61, p. 4860, 1986.
IEEE
Transactions on Magnetics, 1983. v. 19, n. 5, p. 21832185, 1983.
JILES D. C.; ATHERTON, D. L. Ferromagnetic hysteresis.
Propriedades Magnéticas de aços para ns
Eléctricos. 1st. ed. Rio de Janeiro: In I. Bott, P. Rios, & R. Paranhos,
LANDGRAF, F. J.
2002.
LANDGRAF, F. J.; EMURA, M.; CAMPOS, M. F. . On the steinmetz
hysteresis law.
Journal of Magnetism and Magnetic Materials,
2008. v. 320, p. 531534, 2008.
LIORZOU, F.; PHELPS, B.; ATHERTON, D. L. Macroscopic models
of magnetization.
IEEE Transactions on Magnetics,
2000. v. 36,
n. 2, p. 418428, 2000.
Estudo de aplicações da liga Fe78B13Si9
amorfa em núcleos de transformadores de baixa potência. Tese
LUCIANO, B. A.
(Doutorado) Universidade Federal da Paraíba, 1995.
MARTIGNONI, A.
Transformadores. São Paulo:
Globo, 1969.
220
MAZAURIC,
V.;
MALOBERTI,
O.;
MEUNIER,
G.;
KEDOUS-
LEBOUC, A.; GEOFFROY, O.; REBIERE, Y. An energy-based model for dynamic hysteresis.
IEEE Transactions on Magnetics, 2005.
v. 41, n. 10, p. 37663769, 2005.
Finite Element Method Magnetics, version 4.2,
user's manual. [S.l.], 2015. Disponível em: <http://femm.berlios.
MEEKER, D.
de>.
MOSES, A. J. Electrical steels: past, present and future developments.
IEEE Proceedings, 1990. v. 137, n. 5, p. 233245, 1990.
NAIDU, S. R. Simulation of the hysteresis phenomenon using Preisach's
theory.
IEE Proceedings, 1990. v. 137A, n. 2, p. 321329, 1990.
NOGUEIRA, A.; BOUDEC, M. Computer-aided analysis of gapped-
core inductors operating under a wide range of excitations. In: 2nd
International Conference on Electrical Engineering ISBN 978972-99064-4-2. Coimbra, Portugal: [s.n.], 2007.
NOGUEIRA, A.; SALAS, L. M. Analysis of ac contactors combining
electric circuits, time-harmonic nite element simulations and experi-
International Journal of Research and Reviews in
Applied Sciences., 2013. 2013.
mental work.
NOGUEIRA, A. F. L.; PEREIRA JR, D. C. B. Design optimization of
actuator-type devices operating under magnetic saturation. In:
pósio Brasileiro de Sistemas Elétricos.
Sim-
Campina Grande: [s.n.],
2006.
OSSART, F.; MEUNIER, G. Comparison between various hysteresis
models and experimental data.
IEEE Transactions on Magnetics,
1990. v. 26, n. 5, p. 28372839, 1990.
PARKER, R. J.
Advances in Permanent Magnetism.
New York:
John Wiley & Sons, Inc., 1990.
Sistema automatizado de medição e
análise das popriedades magnéticas de materiais utilizando o
quadro de epstein. 2011.
PEREIRA JUNIOR, I. A.
Modélisation de le hystéresis par le modÈle de JilesAtherton. Relatório à preparação de D.E.A. Toulouse, França:
PEUGET.
[s.n.], 1995.
221
PFÜTZNER, H.; SCHÖNHUBER, P. On the problem of eld detection
for single sheet testers.
IEEE Transactions on Magnetics,
1991.
v. 27, n. 2, p. 771775, 1991.
PREISACH, F. Über die magnetische nachwirkung.
Physik, 1935. v. 94, p. 277302, 1935.
Zeitschrift für
Matériaux de le Électrotechnique (Traité d Électricité). 3éme. ed. Lausanne: Presses polytechniques romandes, 1989.
ROBERT, P.
SAY, M. G.
Alternating Current Machines. 5th. ed. Great Britain:
Longman Scientic & Technical, 1983. 35-37 p.
Desenvolvimento de um instrumento virtual
para a determinação do comportamento magnético de transformadores com núcleo de liga amorfa (hardware). Campina
SILVA, L. E. B.
Grande, 1995. Relatório Final de Bolsa de Iniciação Cientíca.
SILVESTER, P.; CHARI, M. Finite element solution of saturable mag-
netic eld problems. IEEE Transactions on Power Apparatus and
Systems, 1970. PAS-89, n. 7, p. 1642 1651, 1970.
SILVESTER, P.; FERRARI, R.
gineers. 2nd. ed. Great Britain:
Finite elements for electrical enCambridge University Press, 1990.
Equipamentos Magnetelétricos: Transdutores,
Transformadores e Máquinas. Rio de Janeiro: Livros Técnicos e
SLEMON, G. R.
Cientícos Editora S.A., 1974.
STOLL, R. L.
The analysis of eddy currents.
Oxford: Clarendon
Press, 1974.
VIEIRA, G. A.; PINTO, M. F.; TEIXEIRA, J. M.; FRAGA, B. L.;
SILVEIRA, F. S.; OLIVEIRA, R. W.
Materiais amorfos. [S.l.]:
Uni-
versidade Federal de Minas Gerais, 2000.
WILLIAMS, H.; BORZORTH, R. M.; SHOCKLEY, W. Magnetic domain on patterns single crystals of silicon iron.
Physical Review,
1949. v. 75, p. 155178, 1949.
WILLIAMS, H. J.; SHOCKLEY, W.; KITTEL, C. Studies of the propagation velocity of a ferromagnetic domain boundary.
view, 1950. v. 84, n. 9, p. 10901094, 1950.
Physical Re-
222
ANEXO A -- LAÇO DE HISTERESE MAGNÉTICA FUNDAMENTAÇÃO TEÓRICA
O campo produzido em uma amostra de forma cilíndrica, inserida ao longo do eixo de um solenóide é aproximadamente uniforme na
região central do cilindro, mas bastante distorcido nas extremidades.
Já para uma amostra em forma de toroide ou anel cilíndrico, o campo
é aproximadamente uniforme em todo o volume e dirigido circunferencialmente. Existe, no caso, uma dependência do campo
à distância
r
H
em relação
do centro do toroide dada por
H =
NI
2πr
.
(A.1)
Se o diâmetro do toroide for grande em comparação com a área
da seção transversal da amostra, pode-se fazer
r
igual ao raio médio do
toroide e usar a equação A.1 para calcular a intensidade de campo.
É comum na literatura do Eletromagnetismo Aplicado considerar o exemplo de um núcleo toroidal como o mostrado na Figura A.1
para explicar os processos de obtenção do laço de histerese.
O com-
portamento de um material magnético submetido a uma variação do
campo magnetizante
H
depende fortemente de seu estado inicial de
magnetização. Entretanto, se o material é submetido a um campo sucientemente intenso,
H1 ,
como mostrado na gura A.2 e esse campo
é revertido um certo número de vezes, o material entra em um estado
cíclico. É como se o material tivesse perdido a memória do estado inicial. Esse aspecto tem que ser levado em consideração no levantamento
experimental de curvas no plano (BH ), tais como a curva inicial de
magnetização e curva normal de magnetização (SLEMON, 1974).
Circuitos magnéticos como o ilustrado na Figura A.1 são utilizados para demonstrar que a área envolvida pelo laço de histerese está
relacionada à energia dissipada sob forma de calor no material magnético (GRAY, 1989; HAMMOND, 1986; PARKER, 1990). Partindo-se
de uma variação innitesimal da força magnetomotriz
N dI , chega-se à
seguinte expressão para a variação da energia suprida pela fonte elétrica
dW = (2πrA)H dB.
Como
2πrA
(A.2)
V
de material magnético, a
dW = V H dB.
(A.3)
representa o volume
equação acima pode ser expressa como
224
Figura A.1 Circuito magnético com núcleo toroidal
Fonte: produção do autor
Figura A.2 Laço de histerese.
Fonte: produção do autor
A energia associada a um ciclo completo é obtida a partir da
integral cíclica
I
W =V
H dB.
(A.4)
225
A equação acima mostra que a energia por unidade de volume
dissipada em um ciclo completo de histerese pode ser calculada pela
área interna do laço.
Essa dissipação de energia tem várias causas.
Estas incluem correntes parasitas localizadas e atrito causado pela presença de impurezas no material (HAMMOND, 1971).
A aquisição de apenas dois sinais elétricos é suciente para a obtenção e posterior processamento numérico do laço de histerese (SILVA,
1995; LUCIANO, 1995). Um dos sinais deve ser proporcional à densidade de uxo
B , o outro proporcional à intensidade de campo H .
Para
a aquisição do laço de histerese foram utilizados dois sinais de tensão,
obtidos a partir da montagem mostrada na Figura A.3.
Figura A.3 Montagem para aquisição do laço de histerese.
Fonte: produção do autor
Na escolha da montagem, procurou-se levar em consideração aspectos de natureza econômica, bem como a facilidade de implementação. A montagem ilustrada é baseada naquelas propostas por (DRAPER, 1963; GROSSNER, 1983). No trabalho em laboratório, foi utilizado um autotransformador variável (Variac) de 500 VA, 0-220 V para
alimentar o primário do transformador em teste. O resistor
R2
empre-
gado na montagem deve ter valor elevado, de maneira que o secundário
do transformador opere como um circuito aberto. Desse modo, a corrente que circula no circuito primário é a corrente de excitação, cujo
sinal é obtido indiretamente, através da tensão sobre o resistor
R1 .
Com o secundário operando como um circuito aberto, o transformador em teste se comporta como um indutor não linear, com baixo
226
nível de dispersão magnética.
Assim, o circuito primário apresenta
comportamento análogo ao do circuito magnético da Figura A.1 e a
intensidade de campo
H
pode ser aproximada pela expressão:
N1 iφ
H =
lm
,
(A.5)
N1 é o número de espiras do enrolamento primário, iφ é a corrente
lm é o comprimento médio do núcleo. Uma vez que
iφ = VR1 /R1 , pode-se expressar a intensidade de campo H em função
da tensão sobre o resistor R1 ,
onde
de excitação e
H =
N1
lm R1
VR1 .
(A.6)
Para se obter um sinal elétrico proporcional à densidade de uxo
B,
pode-se partir das expressões da tensão induzida e corrente no se-
cundário. A tensão induzida no secundário pode ser expressa como
e2 = N2
dφ
dt
.
(A.7)
A corrente no secundário é
ic =
e2
e os valores dos componentes
(A.8)
1
jωC
R2 +
R2
e
C
devem ser escolhidos de
forma que
R2 1
jωC
.
(A.9)
Com isso, a expressão da corrente no secundário pode ser aproximada por
ic ≈
e2
R2
..
(A.10)
Substituindo (A.7) em (A.10), obtém-se:
ic =
N2 dφ
R2 dt
.
(A.11)
Integrando-se a relação acima no tempo, tem-se:
Z
Z
ic dt =
N2
R2
dφ.
(A.12)
227
Como
R
ic dt
Q = Vc C
representa a carga
armazenada no ca-
pacitor, pode-se escrever:
N2
Vc =
φ.
R2
(A.13)
O uxo magnético pode ser expresso em função da tensão sobre
o capacitor
R2 C
φ=
N2
Fazendo-se uso da relação
Vc .
(A.14)
φ = BA,
chega-se, nalmente, à
relação:
B=
R2 C
N2 A
Vc ,
(A.15)
ou seja, uma relação entre a densidade de uxo
B
e o sinal de tensão
sobre o capacitor.
VR1
Tomando-se o sinal de tensão
o sinal de tensão
no modo
XY
Vc
no canal
Y,
no canal
X
do osciloscópio e
faz-se a composição desses dois sinais
e se obtém o laço de histerese.
A densidade de energia dissipada em cada ciclo é calculada pela
relação:
Z
W =
H dB.
(A.16)
Substituindo as expressões A.6 e A.15 em A.16 chega-se a:
W =
O termo
H
N1 R2 C
I
N2 R1 Alm
VR1 dVc .
(A.17)
VR1 dVc representa a área interna do ciclo. Essa área,
N1 R2 C/(N2 R1 Alm ), for-
quando multiplicada pelo termo constante
nece a energia por unidade de volume.
O volume médio do transformador é
em cada ciclo é:
W =C
Se
f
N1 R2
Alm ,
e a energia dissipada
I
VR1 dVc .
N2 R1
(A.18)
é a frequência de rede, a potência média dissipada pode ser
obtida por:
W = fC
N1 R2
N2 R1
I
VR1 dVc .
(A.19)
228
ANEXO B -- MODELO DE JILES E ATHERTOM
Pontos notáveis da curva experimental proposto por Jiles e Athertom (JILES D. C.; ATHERTON, 1983) como valores iniciais para o
algoritmo de otimização de parametros
M = Mirr + Mrev ,
(B.1)
Mrev = c(Man − Mirr ),
a
He
−
,
Man = Ms coth
a
He
Man − Mirr
dMirr
=
,
dHe
kδ
He = H + αM.
As constantes
Ms , a, c, k e α são os
δ uma variável
um laço de histerese , sendo
(B.2)
(B.3)
(B.4)
(B.5)
parâmetros próprios para
condicional representante
do sentido da evolução da magnetização:
δ=

 +1
para
dH
dt
≥0
−1
para
dH
dt
<0

.
(B.6)
B.1 PARÂMETROS DO ALGORITMO DE JILES
Nessa seção, apresentam-se os parâmetros do modelo de Jiles.
B.1.1 Susceptibilidade diferencial
Jiles utiliza a susceptibilidade diferencial como uma ferramenta
para deduzir e encontrar algumas das equações, e denir os seus respectivos valores pontuais:
χ=
lim
∆H,∆M →0
∆M
∆H
=
dM
dH
.
(B.7)
230
B.1.2 O parâmetro Ms
Ms
Segundo Jiles (JILES D. C.; ATHERTON, 1983),
[A/m] é o
parâmetro mais fácil de ser obtido, correspondendo à magnetização de
saturação e sendo uma característica conhecida para um certo material.
B.1.3 O parâmetro k
k
O parâmetro
[A/m] expressa quanto as paredes dos domínios
estão presas na estrutura metalúrgica do material, dicultando o deslocamento e a manutenção de uma homogeneidade magnética no processo
de magnetização (JILES D. C.; ATHERTON, 1983).
Pode ser aproximado pelo valor do campo coercitivo
Hc
dado
por:
k ≈ Hc
ou
(B.8)

k=

Man Hc 
α +
1−c 

1−c
.
dMan Hc 
χc − c
dH
(B.9)
B.1.4 O parâmetro α
O parâmetro
αé
um fator representante do acoplamento entre
domínios magnéticos (JILES D. C.; ATHERTON, 1983), utilizado inicialmente por Weiss. Ele é determinado no ponto em que é denido o
conceito de indução remanente
Br , ou
χr .
magnetização remanente
Mr ,
onde se obtém a susceptibilidade
Mr = Man Mr +
k
α
1−c
−
χr − c
1
dMan Mr
dH
.
(B.10)
231
B.1.5 O parâmetro a
O parâmetro
tante de Boltzmann
a [A/m] está relacionado diretamente com a consκ e a temperatura, e inversamente com o momento
magnético (JILES D. C.; ATHERTON, 1983).
Mm = Man Hm −
O parâmetro
versível
a,
Mver
c
(1 − c)kχm
αχm + 1
obtém se o valor do coeciente
H→0+
(B.11)
No modelo, a componente de magnetização re-
é determinada pelo coeciente
χin = lim
.
c
c.
Conhecendo-se
Ms
e
diretamente.
dMan Ms
=c
=c
.
∆H
dH M →0+
3a
∆M
(B.12)
A equação (B.12) é utilizada como uma restrição para os parâmetros
a
e
α.
A susceptibilidade
Xna
é a susceptibilidade sem histerese na
origem (curva sem histerese).
B.2 ALGORITMO DE JILES
Nessa seção apresenta-se o algoritmo de Jiles.
232
Figura B.1 Algoritmo principal de obtenção dos parâmetros proposto
por Peuget.
Fonte: adaptado de (BATISTELA, 2001)
233
Figura B.2 Algoritmo da subrotina do método da secante para obtenção do parâmetro
α.
Fonte: adaptado de (BATISTELA, 2001)
234
Figura B.3 Algoritmo da subrotina do método da secante para obtenção do parâmetro
a.
Fonte: adaptado de (BATISTELA, 2001)
ANEXO C -- METODOLOGIA DE CONSTRUÇÃO DE UM
TRANSFORMADOR MONOFÁSICO
Este anexo apresenta um roteiro para projeto de transformadores
monofásicos baseado em (MARTIGNONI, 1969).
C.1 SEÇÃO GEOMÉTRICA DO NÚCLEO (SGN )
Sgn = a · b [cm2 ]
a:
b:
(C.1)
largura da coluna central em cm;
espessura do núcleo em cm.
a = 2, 9 [cm]
a = 2, 9 [cm]
Sgn = 8, 41 [cm2 ]
C.2 SEÇÃO MAGNÉTICA DO NÚCLEO (SM N )
Smn = Sgn · Fu [cm2 ]
Sgn : Seção Geométrica do Núcleo;
Fu : Fator de utilização. Número que varia
(C.2)
entre 0,8 e 0,9, dependendo
do estado de conservação das chapas.
Sgn = 8, 41 [cm]
Fu = 0, 9
Smn = 7, 6 [cm2 ]
C.3 POTÊNCIA DO NÚCLEO OU POTÊNCIA DO PRIMÁRIO (S1 )
S1 = (Smn )2 [VA]
Smn :
2
Seção magnética do núcleo (cm );
Smn = 7, 6 [cm2 ]
(C.3)
236
S1 = 58 VA
C.4 POTÊNCIA DO SECUNDÁRIO (S2 )
A potência do secundário é inferior a potência do primário, devido às perdas internas no transformador.
S2 =
S1 :
S1
1, 1
[VA]
(C.4)
Potência do Primário (VA);
1,1: constante provenientes das perdas internas no transformador.
S1 = 58 [VA]
S2 = 53 [VA]
C.5 CORRENTE DO PRIMÁRIO (I1 )
I1 =
S1 :
V1 :
S1
V1
[A].
(C.5)
Potência do primário (VA);
Tensão do primário (V).
Tem-se que:
I1 =
S1
220
S1 = 58 [VA]
V1 = 220 [V]
I1 = 0, 26 [A] → I1,pk = 0, 3676 [A]
C.6 CORRENTE DO SECUNDÁRIO (I2 )
I2 =
S2
V2
[A].
(C.6)
237
S2 :
V2 :
Potência do secundário (VA);
Tensão do secundário (V).
I2 =
S2
V2
= 2, 2 [A] → I2,pk = 3, 1112 [A]
Observação: Quando o enrolamento secundário possuir mais de uma
tensão, devemos calcular a corrente correspondente a cada tensão.
C.7 SEÇÃO DO FIO DO ENROLAMENTO PRIMÁRIO (S1C )
S1c =
I1
d
[mm2 ]
(C.7)
I1 : Corrente do enrolamento primário (A);
d: Densidade de corrente ( A/mm2 ), escolher-se-á um valor entre os
2
limites de 3 a 6 A/mm .
S1c : Seção calculada do enrolamento primário ( [mm2 ]);
S1r : Seção real do enrolamento primário, obtida mediante consulta a
tabela de os.
S1c =
I1
(C.8)
d
I1 = 0, 26 [A]
d = 5 [A/mm2 ]
S1c = 0, 052 [mm2 ]
S1r = 0, 081 [mm2 ]
(só há um tipo de bitola para primário AWG 28 (0,081)
C.8 SEÇÃO DO FIO DO ENROLAMENTO SECUNDÁRIO
(S2C )
S2c =
I2
d
[mm2 ]
I2 : Corrente do enrolamento secundário (A);
d: Densidade de corrente ( A/mm2 ), escolher-se-á
(C.9)
um valor entre os
238
limites de 3 a 6
S2c :
S2r :
A/mm2 .
Seção calculada do enrolamento secundário (
[mm2 ]);
Seção real do enrolamento secundário, obtida mediante consulta
a tabela de os.
S1c =
I1
(C.10)
d
I2 = 2, 2 [[A]]
d = 5 [A/mm2 ]
S2c = 0, 44 [mm2 ]
S2r = 0, 33 [mm2 ]
só se dispõem de o 0,33
[mm2 ].
C.9 DENSIDADE REAL DE CORRENTE DO PRIMÁRIO
(DR1 )
dr1 =
I1
S1r
[A/mm2 ]
I1 : Corrente do enrolamento primário (A);
S1r : Seção real do enrolamento primário.
dr1 : Densidade de corrente real ( A/mm2 ),
2
limites de 3 a 6 A/mm .
(C.11)
deve permanecer entre os
Observação: Quando o enrolamento primário possuir mais de um valor
de tensão, logo, mais de um valor de corrente devemos calcular todas
as densidades correspondentes, tendo então.
I1 = 0, 26 [A]
S1r = 0, 081 [mm2 ]
dr1 = 3, 2 [A/mm2 ]
239
C.10 DENSIDADE REAL DE CORRENTE DO SECUNDÁRIO (DR2 )
dr2 =
I2
S2r
[A/mm2 ]
I2 : Corrente do enrolamento secundário (A);
S2r : Seção real do enrolamento secundário.
dr2 : Densidade de corrente real ( A/mm2 ), deve
2
limites de 6 a 9 A/mm .
Observação:
(C.12)
permanecer entre os
Quando o enrolamento secundário possuir mais de um
valor de tensão, logo, mais de um valor de corrente devemos calcular
todas as densidades correspondentes, tendo então.
I2 = 2, 2 [A]
S2r = 0, 33 [mm2 ]
dr2 = 6, 7 [A/mm2 ]
C.11 NÚMERO DE ESPIRAS DO ENROLAMENTO PRIMÁRIO (N1 )
N1 =
V1 · 108
4, 44f BSmn
[espiras]
V1 : Tensão do enrolamento primário (V);
f : Freqüência (60 Hz);
B : Indução magnética, valor entre 10.000
(C.13)
e 11.000 Gauss.
Sm n = 7, 6 [cm2 ]
Observação: Se as chapas do núcleo forem de boa qualidade usa-se
11.000
Gauss, caso contrário
B = 10.000
B=
Gauss. Se o enrolamento
primário possuir outras tensões, podemos determinar o seu número de
espiras aplicando a fórmula acima ou pela relação:
V1 = 220 [V]
f = 60 [Hz]
240
B = 10000 [Gauss]
Smn = 7, 6 [cm2 ]
N1 = 1087 ≈ 1100 [espiras]
C.12 NÚMERO DE ESPIRAS DO ENROLAMENTO SECUNDÁRIO (N2 )
N2 =
V2 · 108
4, 44f BSmn
[espiras]
V2 : Tensão do enrolamento secundário (V);
f : Frequência (60 Hz);
B : Indução magnética, valor entre 10.000 e 11.000
(C.14)
Gauss.
Sm n = 7, 6 [cm2 ]
Observação: Se as chapas do núcleo forem de boa qualidade usa-se
11.000
Gauss, caso contrário
B = 10.000
B=
Gauss. Se o enrolamento
primário possuir outras tensões, podemos determinar o seu número de
espiras aplicando a fórmula acima ou pela relação:
V1 = 24 [V]
f = 60 [Hz]
B = 10000 [Gauss]
Smn = 7, 6 [cm2 ]
N1 = 119 ≈ 120 [espiras]
ANEXO D -- FORMAS DE ONDA
Figura D.1 Corrente do ensaio à vazio (I1
0 [mA])
Fonte: produção do autor
= 50 [mA]
e
I2 =
242
Figura D.2 Corrente do ensaio de curto-circuito (I1
I2 = 1936 [mA]
e
a = 7, 42)
Fonte: produção do autor
= 300 [mA],
243
Figura D.3 Corrente de Inrush
Fonte: produção do autor
244
ANEXO E -- ARTIGOS DESENVOLVIDOS AO LONGO
DO TRABALHO
ANALYTICAL AND FINITE-ELEMENT CALCULATION OF MAGNETIC FORCES ON AC CONTACTORS
[DEVICES]
Antônio Flavio Licarião Nogueira and Leonardo Jose Amador Salas
Maldonado and F. C. Schulz
Universidade do Estado de Santa Catarina, Joinville, Santa Catarina,
Brazil
ABSTRACT
The paper addresses the theoretical basis of the
magnetic forces generated in dc and ac contactors.
Keywords:
contactor, contact bounce, nite element analysis,
magnetic forces, shading ring.
THE PRINCIPLE OF DUALITY BETWEEN ELECTRIC AND MAGNETIC CIRCUITS APPLIED TO THE
ANALYSIS OF ELECTROMAGNETIC DEVICES / THE
USE OF FEA TO OVERCOME THE LIMITATIONS OF
THE CLASSICAL MAGNETIC CIRCUIT ANALYSIS
Antônio Flavio Licarião Nogueira and Leonardo Jose Amador Salas
Maldonado
Universidade do Estado de Santa Catarina, Joinville, Santa Catarina,
Brazil
ABSTRACT The paper addresses complementary approaches
to the calculation of electromagnetic parameters of an industrial alternating current (AC) contactor rated for 220 volts and 60 hertz. The
methods of analysis include conventional electric circuits derived from
measurements of terminal characteristics. The duality between interlinked electric and magnetic circuits is employed to calculate the contactor's magnetizing reactance during a locked closing maneuver and
during the closed-core conguration.
The parameters obtained from
the circuit analyses are compared to the more precise estimates of nite
element analyses. Special attention is given to the subtle dierences of
circuit properties applied to the conductive regions containing driving
currents as well as to regions where current is actually induced due
to time variation of the magnetic ux. Attempt is made to facilitate
the understanding of the physical phenomena related to the presence
of eddy currents in the shading rings.
246
Keywords:
Contactor, Duality model, Finite element analysis,
Magnetic circuits, Magnetic forces.
ANALYSIS OF AC CONTACTORS COMBINING ELECTRIC CIRCUITS, TIME-HARMONIC FINITE ELEMENT
SIMULATIONS AND EXPERIMENTAL WORK
Antônio Flavio Licarião Nogueira and Leonardo Jose Amador Salas
Maldonado
Universidade do Estado de Santa Catarina, Joinville, Santa Catarina,
Brazil
ABSTRACT The paper addresses complementary approaches
to the calculation of electromagnetic parameters of an industrial alternating current (AC) contactor rated for 220 volts and 60 hertz. The
methods of analysis include conventional electric circuits derived from
measurements of terminal characteristics. The duality between interlinked electric and magnetic circuits is employed to calculate the contactor's magnetizing reactance during a locked closing maneuver and
during the closed-core conguration.
The parameters obtained from
the circuit analyses are compared to the more precise estimates of nite
element analyses. Special attention is given to the subtle dierences of
circuit properties applied to the conductive regions containing driving
currents as well as to regions where current is actually induced due
to time variation of the magnetic ux. Attempt is made to facilitate
the understanding of the physical phenomena related to the presence
of eddy currents in the shading rings.
Keywords:
Contactor, Finite element analysis, Magnetic cir-
cuits, Magnetic forces, Shading ring.
ANEXO F -- PROGRAMAÇÃO EM LUA
Neste anexo, é apresentada a programação em Lua desenvolvida
para operar o FEMM.
F.1 CURVA DE HISTERESE E PERDA A VAZIO NO TRANSFORMADOR
print("Curva BH e perdida de ferro trafo a vazio")
print ("t i1 i2 B H Wh")
for t=0,100,1 do
i1= t/1000+ 0.00000001A CORRENTE NÃO PODE SER ZERO
i2= 9.17*0
mi_modifycircprop("primario",1,i1)entre aspas o nome do circuito
mi_modifycircprop("secundario",1,i2)
mi_analyze(0) iniciar os calculos
mi_selectgroup(2)corresponde ao bobibado primario
mi_loadsolution() Carrega Pós processador
mo_addcontour(0,34.5)
mo_addcontour(14.2,34.5)
A= mo_lineintegral(0)
B=A/0.000406
mi_analyze(0)
mi_selectgroup(3)corresponde ao bobinado secundario
mi_loadsolution() Carrega Pós processador
mo_addcontour(7.4,7.7)
mo_addcontour (35.2,7.7)
mo_addcontour(35.2,7.7)
mo_addcontour(35.2,64.3)
mo_addcontour(35.2,64.3)
mo_addcontour(7.4,64.3)
mo_addcontour(7.4,64.3)
mo_addcontour (7.4,7.7)
C= mo_lineintegral(1)
H=C/0.1688
mi_analyze(0)
mi_selectgroup(1)corresponde ao nucleo
mi_loadsolution() Carrega Pós processador
mo_groupselectblock(1) nucleo onde sera feito o calculo
wh=mo_blockintegral(3)perdidas de histerese
print(format("%.2f %.4f %.4f %.8f %.8f %.8f",t,i1,i2,B,H,wh ))
248
mo_close()
end
F.2 INDUTÂNCIA ATRAVÉS DE VETOR DE POTENCIAL
MAGNÉTICO COM SECUNDÁRIO COM CARGA
print("Indutancia no tranformador com secundario com carga")
print ("t i1 AJ1 I2 AJ2")
for t=0.00000000001,100,1 do
i1= (0.3677 + 0.052)*t/100 A CORRENTE NÃO PODE SER ZERO
i2= 0.3677*9.17*t/100
mi_modifycircprop("primario",1,i1)entre aspas o nome do circuito a
ser modicado
mi_modifycircprop("secundario",1,i2)
mi_analyze(0) inicie calculo
mi_selectgroup(2)corresponde ao bobibado primario selecione a parte
do circuito que sera analizada
mi_loadsolution() Carrega Pós processador
mo_groupselectblock(2)selecione o que va a ser operado
k= mo_blockintegral(0)calcule a in tegral de potencial mag AJ bob
primaria
mi_analyze(0)
mi_selectgroup(3)corresponde ao bobinado secundario
mi_loadsolution() Carrega Pós processador
mo_groupselectblock(3)
M= mo_blockintegral(0)vetor potencial mag AJ bob secundaria
print(format("%.3f %.4f %.8f %.4f %.8f ",t,i1, k ,i2,M ))
mo_close()
end
F.3 CÁLCULO DE FORÇA NO CONTACTOR
Rotina para trasladar objeto direção y
print("Iteração Tensor de força cc Tensor fortça CA distancia")
for i=1,2,1 do
dy= 0.1*i
mi_selectgroup(1)
mi_movetranslate(0,-dy,(4))
249
mi_analyze(0)
mi_loadsolution() Carrega Pós processador
mo_groupselectblock(1)
print(format("%.1f %.8f %.8f %.2f", i,
mo_blockintegral(19),mo_blockintegral(21),dy ))
mo_close()
end
F.4 ROTINA PARA ROTACIONAR OBJETO
print("rutina para rotar")
for i=1,2,1 do
alfa= 5*i
mi_selectgroup(1)
mi_moverotate(0,0,alfa,(4))
mi_analyze(0)
mi_loadsolution() Carrega Pós processador
mo_groupselectblock(1)
print(format("%.1f %.8f %.8f %.8f %.8f %.1f", alfa,
mo_blockintegral(18),mo_blockintegral(19),mo_blockintegral(20),
mo_blockintegral(21),i ))
mo_close()
end
250
ANEXO G -- MODELOS DE PERDAS EXCEDENTES DE
BERTOTTI E CONCEITO DE OBJETO MAGNÉTICO
(OM)
G. Bertotti (BERTOTTI, 1983, 1984) abordou de uma forma
estatística o processo de magnetização dinâmica e as perdas por excesso.
Ele deniu uma nova entidade física, o objeto magnético ou OM, pelo
qual a magnetização se inverte. A noção dos OMs e a justicação se
deve ao fato de que o deslocamento de uma parede, ou segmento de
parede, a qual é a origem da variação da magnetização no material,
não pode ser feita de forma isolada.
OM (peça de domino) é o ente conceitual responsável por toda
a modicação da magnetização, e por conseqüência das perdas do material causadas pelo fenômeno de magnetização.
Assim, o estado magnético do material será caracterizado pelo
número de OMs que participam do processo de magnetização (chamados OMs ativos, na analogia todas as peças que mudaram sua posição)
Seja uma lâmina magnética de condutividade ϕ e seção magnéS , submetida a uma indução periódica alternada B(t), de freqüência f e de valor máximo Bm . A cada instante t, a variação da indução
é gerada por um número nom (t) de OMs, aqueles que participam do
processo de magnetização. Seja He (t), chamado de campo por excesso,
tica
a parte necessária do campo aplicado para contrabalançar o campo de
frenagem produzido pelas correntes induzidas dos OMs em movimento(
lei de Lenz). O valor médio das perdas por excesso produzidas nas lâminas pelos
nom (t) OMs ativos é expresso pela equação (G.1),baseada
na equação de perdas na curva BH proposta por Bertotti (BERTOTTI,
1985) e Fiorillo (FIORILLO; NOVIKOV, 1990).
We =
1
T
Z
T
He (t)
0
∂B(t)
∂t
dt [J].
(G.1)
A questão é como determinar este campo de excesso
He (t).
De
acordo com o trabalho de Williams et al (WILLIAMS; SHOCKLEY;
KITTEL, 1950), o campo magnético necessário para que uma parede
se desloque é proporcional a velocidade da variação do uxo induzido
pelo movimento da parede.
He(t)
dφ/dt indu-
Neste caso, o campo por excesso
será proporcional a velocidade da variação do uxo local
zido pelo deslocamento do OM. Esta proporcionalidade é expressa pela
252
equação (G.2), onde
G
representa o coeciente de atrito do OM, igual
a 0,136 no caso onde o OM corresponde a uma parede (AMAR, 1994).
He (t) = Gσ
dφ
(G.2)
dt
dφ/dt
Quando cada OM participa com uma variação
no pro-
cesso global de magnetização, a velocidade da variação do uxo global
S dB/dt
resulta da contribuição do número
nom (t)
dos Oms ativos.
Isto é formulado na equação
S
dB(t)
dt
= nom (t)
dφ(t)
(G.3)
dt
e, por consequência
He (t) = σGS
1
dB(t)
nom (t)
dt
.
(G.4)
Esta relação é traduzida pela Equação (G.5), onde o parâmetro
Vo
equivale a um campo coercitivo e caracteriza a oposição dos
OMs a se ativar, quando inuenciados por um campo externo aplicado.
Considerando
nom (t) =
He (t)
Vo
(G.5)
tem-se que
We =
1 p
f mv
σGVo S
1
T
Z
T
0
dB(t) 1,5
dt [J/kg]
dt (G.6)
Para uma indução na forma de onda senoidal, de freqüência f e
valor máximo
Bm , as perdaspor excesso por período são expressas pela
equação (G.7)
We =
p
8, 76363 p
1,5
σGVo S(Bm
f ).
mv
(G.7)