física – paulo lee

FÍSICA – PAULO LEE
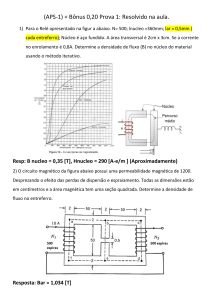
Resistência equivalente entre R2 e R3: R2,3 = 6.3/(6+3) = 2 
Resistência equivalente: Req = R1 + R2,3 = 2 + 2 = 4 .
b) A tensão elétrica nos extremos da associação de resistores.
Como a intensidade de corrente em R2 é i2 = 0,5 A, então a intensidade de corrente no resistor R 3,
que está em paralelo, e tem metade do valor da resistência de R 2 será o dobro, ou seja, i3 = 1 A.
Então, a intensidade de corrente total é igual à soma de i 2 com i3, ou seja, i = 1,5 A. Daí:
U = Req.i
U = 4.1,5
U = 6 V.
c) A resistência interna do gerador.
U = E – r.i
6 = 7,5 – r.1,5
r = 1 .
 = Qq - Qf
50 = Qq – 150
Qq = 200 cal
=
/Qq
 = 50/200
 = 0,25   =25 %
b) A temperatura prevista para a fonte fria, em graus Celsius.
Tq = 127 + 273 = 400 K
 = 1 – Tf /Tq
0,25 =1 – Tf/400
Tf/400 = 0,75
Tf = 300 K  Tf = 27 oC.
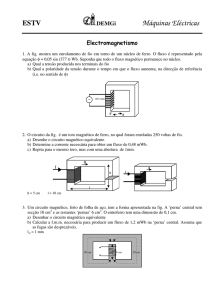
Pelo sentido convencional da corrente elétrica, que sai do polo positivo da bateria, é
possível, usando a regra da mão-direita, determinar o sentido do campo magnético no núcleo
interno do solenoide, e portanto, descobrir o poço norte (de onde as linhas do campo magnético
saem das espiras). Daí, determinam-se os polos no entreferro do núcleo, conforme a figura. As
linhas do campo magnético deste entreferro saem do polo norte e chegam no polo sul (de baixo
para cima).
b) Qual é, por ação do campo magnético, o comportamento da trajetória a ser descrita pelos
elétrons no núcleo de ferro no início do movimento no entreferro? Indicar também o sentido do
movimento a ser executado. Justifique sua resposta.
Como os elétrons penetram perpendicularmente às linhas do campo magnético no
entreferro, suposto uniforme, podemos concluir que, com o uso da regra da mão-esquerda, os
elétrons recebem força perpendicular ao plano da folha, com sentindo entrando na mesma,
tendendo a um movimento circular uniforme. Assim, é possível concluir que no início do
movimento dos elétrons, no entreferro, os mesmos tendem a se mover entrando no plano da folha
do desenho.
c) Considerando os valores aproximados, por conveniência de cálculo, para algumas das grandezas
físicas mostradas abaixo, determine a aceleração de cada elétron que penetra no entreferro do
núcleo de ferro se a velocidade deles, ao iniciarem o movimento no entreferro, for de 400 m/s.
Igualando a força magnética com a força centrípeta, encontramos a equação para
determinar o raio da trajetória do movimento circular uniforme:
Dados: B = 0,03 T = 3.10-2 T
e
v = 400 m/s = 4.102 m/s
F m = Fc
q.v.B.sen 900 = m .v2/R  R = m.v/(q.B)
Daí: R = 9.10-31.4.102/(1,5.10-19.3.10-2)  R = 8.10-8 m
Como o movimento é circular uniforme, a aceleração é centrípeta, daí:
ac = v2/R = (4.102)2/(8.10-8)
ac = 2.1012 m/s2.