0 = v 0 = v v . 0 − vv vv =1 0 = v 0 = v - DECOM

EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 8
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 8
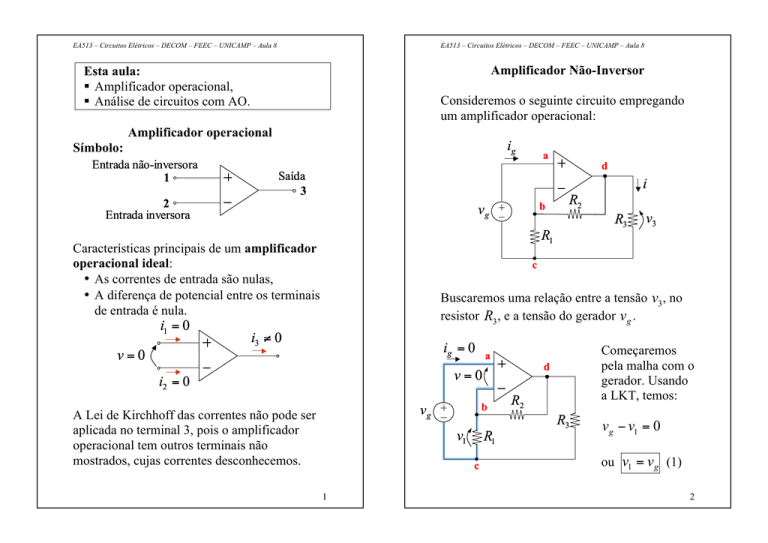
Amplificador Não-Inversor
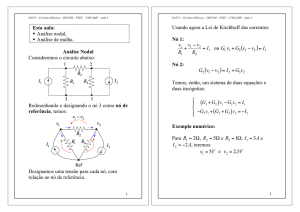
Esta aula:
! Amplificador operacional,
! Análise de circuitos com AO.
Consideremos o seguinte circuito empregando
um amplificador operacional:
Amplificador operacional
ig
Símbolo:
Entrada não-inversora
1
2
Entrada inversora
Saída
3
v=0
d
i
b
vg
R2
R3
R1
Características principais de um amplificador
operacional ideal:
• As correntes de entrada são nulas,
• A diferença de potencial entre os terminais
de entrada é nula.
i1 = 0
a
v3
c
Buscaremos uma relação entre a tensão v3 , no
resistor R3 , e a tensão do gerador v g .
i3 ≠ 0
ig = 0
a
d
v=0
i2 = 0
b
vg
A Lei de Kirchhoff das correntes não pode ser
aplicada no terminal 3, pois o amplificador
operacional tem outros terminais não
mostrados, cujas correntes desconhecemos.
v1
R1
c
1
Começaremos
pela malha com o
gerador. Usando
a LKT, temos:
R2
R3
vg − v1 = 0
ou v1 = vg (1)
2
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 8
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 8
Substituindo (1) e (2) em (3), tem-se
a
vg
i=0
b
v1
R1
Em seguida,
aplicamos a LKC
no nó b:
d
R2
v2
Portanto, podemos interpretar esse circuito
como contendo uma fonte de tensão
dependente, controlada por outra tensão ( v g ):
v1 v2
+
=0
R1 R2
R3
& R #
v3 = $$1 + 2 !! v g
% R1 "
c
ig = 0
v2 = −
ou
a
vg
b
v1
R1
R2
vg
R1
d
R2
v2
R3
v3
vg
(2)
Finalmente,
aplicamos a
LKT na malha
com R3 :
i
& R2 #
$$1 + !!vg
% R1 "
R3
v3
De fato, esse circuito é um amplificador de
tensão não-inversor de ganho µ = 1 + R2 R1 .
v1 − v2 − v3 = 0
ou
v3 = v1 − v2 (3)
3
4
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 8
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 8
Se fizermos R1 = ∞ e R2 = 0, o ganho é
unitário, e teremos um “seguidor de tensão”,
que isola o circuito conectado à entrada do
circuito conectado à saída.
Amplificador Inversor
Consideremos uma outra configuração
envolvendo um amplificador operacional (note
a posição dos terminais de entrada do
amplificador):
iE = 0
vE
R2
vS
R1
vE
vS
Estamos novamente procurando uma expressão
para a relação vS vE .
R2
v1
vE
5
R1
=0
vS
Aplicando a
LKT na malha
na entrada:
vE = v1 (1)
6
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 8
R1
vE
ou
vS
R1 i1
vE − v1 − v2 − vS = 0
vS = −v2 (2)
v2
v1 i2
Portanto, esse circuito pode ser interpretado
como um amplificador inversor de tensão, de
ganho − R2 R1 .
LKT para a malha
envolvendo ambos
resistores:
R2
v1
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 8
a
ie
R2
Note a corrente de entrada nesse circuito (vista
pelo circuito acoplado à entrada) não é nula, e
vale i1 = vE R1 .
Portanto, um modelo para esse circuito inclui
uma fonte de tensão dependente controlada
por tensão, como mostrado a seguir:
LKC no nó a:
i1
i1 = i2 , pois ie = 0.
Ou:
vE
v1 v2
=
(3)
R1 R2
R1
R2
vE
R1
vS
Aplicando (1) e (2) em (3), temos:
v
vE
=− S
R1
R2
Note que podemos também escrever
v
R
R
→ S = − 2 ou vS = − 2 vE
vE
R1
R1
vS = − R2
7
vE
= − R2 i1,
R1
8
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 8
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 8
o que nos leva a um modelo com uma fonte de
tensão dependente controlada por corrente:
Portanto, sob o ponto de vista dos terminais 3 e
4, temos um resistor de valor R2 em paralelo
com um gerador de corrente i2 = vE R1 :
i1
1
vE
R2 i1
R1
vS
i1
vE
3
R1
vE
R1
R2
2
Vamos agora tomar os terminais 3 e 4
(indicados no circuito) como sendo os terminais
de saída:
vS
4
3
1
vE
R1 i2
R2
i1 ie = 0
2
Relembrando, temos i2 = i1 =
vE
2
9
4
Portanto, podemos construir um modelo
envolvendo na saída uma fonte de corrente
dependente controlada por tensão (a de entrada,
vE ).
Podemos também obter um modelo envolvendo
um gerador de corrente agora controlado por
corrente, usando simplesmente i2 = i1:
1
vE
.
R1
vS
i1
3
R1
i1
R2
vS
4
10
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 8
11