)0( V vC = . → = + 0)()( titiR )( )( tv ti → V I → , τ τ RC =

EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 13
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 13
Portanto, fazendo as correspondências:
Esta aula:
! Circuitos RC sem fontes independentes.
! Circuitos singulares.
i (t ) → v(t ), L
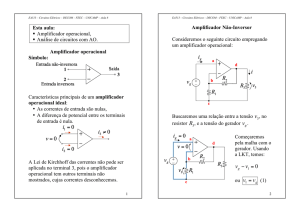
Vamos considerar agora um circuito com um
capacitor carregado e um resistor, sem fonte
independente.
iC (t )
vC (t )
C
R
→ RC e I 0 → V0,
podemos usar a solução do problema com o
circuito RL para o caso do circuito RC:
& t #
v(t ) = V0 exp$ −
!.
% RC "
iR (t )
De fato, os circuitos RC e RL são duais.
v(t ) R
A curva da tensão v(t ) é mostrada abaixo:
Consideraremos vC (0) = V0 .
v(t )
Aplicando a LKC no nó superior, temos
iC (t ) + iR (t ) = 0 → C
V0
dv v
+ = 0.
dt R
Note que a equação diferencial acima tem a
mesma forma matemática que a equação obtida
da análise do circuito RL, ou seja,
di R
R
+ i = 0 → i (t ) = I 0 exp&$ − t #!.
dt L
% L "
1
τ = RC
t
Para o caso do circuito RC, temos τ = RC .
2
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 13
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 13
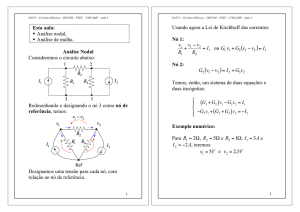
Circuito com chave e sem fonte independente
Escrevendo a LKC para o nó superior, temos
Consideremos o circuito abaixo com dois
capacitores:
C1
t =0
C1 = 1F
v1 (t )
v2 (t )
C2 = 1F
dv1
dv
+ C2 2 = 0 ou C1dv1 = − C2 dv2 .
dt
dt
Integrando essa última equação, no intervalo de
tensões correspondente ao intervalo de tempo
[0− ,0+ ], obtemos
C1[v1 (0 + ) − v1 (0 − )] = − C2 [v2 (0 + ) − v2 (0 − )].
Vamos supor que o capacitor C1 esteja
carregado, com uma tensão de 1 volt entre seus
terminais, e que C2 esteja descarregado.
Usando os valores iniciais das tensões nos
capacitores e os valores das capacitâncias,
ficamos com
A chave será fechada no instante t = 0. Assim,
indicaremos as tensões nos capacitores antes do
fechamento da chave como:
v1 (0 − ) = 1V e v2 (0 − ) = 0V .
v1 (0 + ) − 1 = −v2 (0 + ) → v1 (0 + ) + v2 (0 + ) = 1
Como após o fechamento da chave temos
v1 (0 + ) = v2 (0+ ) , então, resulta em
v1 (0+ ) = v2 (0+ ) = 1 V
2
Estamos interessados nas tensões dos
capacitores logo após o fechamento da chave,
ou seja: v1 (0 + ) = v2 (0 + ) = ?
3
4
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 13
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 13
Vamos agora determinar a energia armazenada
no circuito antes e depois do fechamento da
chave.
Note que a tensão v1 (t ) muda de 1V para 0,5V
no intervalo [0− ,0+ ], ou seja, de duração
infinitesimal.
Antes de fechar a chave ( t = 0− )
Os modelos de capacitores que usamos não
permitem mudanças abruptas de tensão.
Portanto esse modelo não é válido no intervalo
t = [0− ,0+ ].
2
2
1
1
w(0− ) = C1 [v1 (0− )] + C2 [v2 (0− )]
2
2
1
= J
2
1
w(0− ) = J
2
Essa mudança abrupta da tensão de C1 está
associada a uma corrente elevada no circuito
durante o intervalo t = [0− ,0+ ], que provoca a
geração de uma onda eletromagnética, que
irradia a energia de 0,25 J, ficando no circuito
os outros 0,25 J, armazenado nos capacitores.
Depois de fechar a chave ( t = 0+ )
2
2
1
1
w(0+ ) = C1 [v1 (0+ )] + C2 [v2 (0+ )]
2
2
1
w(0+ ) = J
4
Onde foi para 0,25 J após o fechamento da
chave?
5
6