V v - DECOM

EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
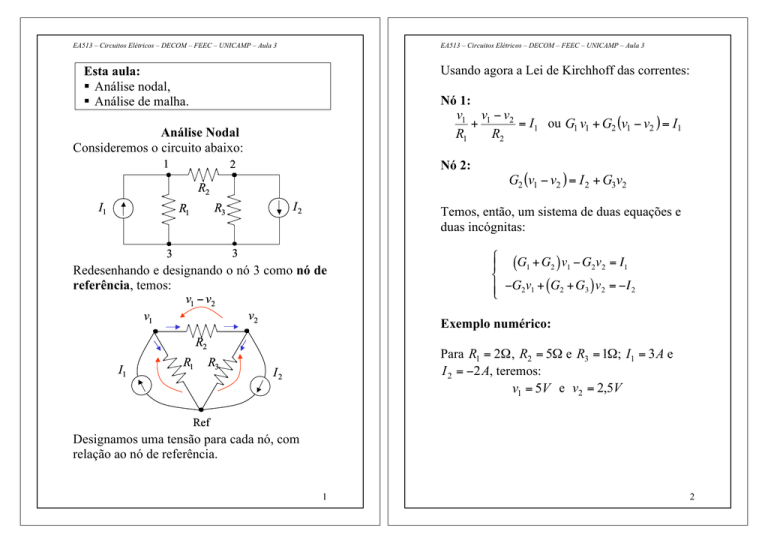
Usando agora a Lei de Kirchhoff das correntes:
Esta aula:
! Análise nodal,
! Análise de malha.
Nó 1:
v1 v1 − v2
+
= I1 ou G1 v1 + G2 (v1 − v2 ) = I1
R1
R2
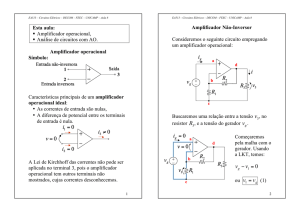
Análise Nodal
Consideremos o circuito abaixo:
1
Nó 2:
2
R2
I1
I2
R3
R1
Temos, então, um sistema de duas equações e
duas incógnitas:
3
3
Redesenhando e designando o nó 3 como nó de
referência, temos:
v1 − v2
v2
v1
R2
I1
R1
R3
G2 (v1 − v2 ) = I 2 + G3v2
" G +G v −G v = I
$ ( 1
2) 1
2 2
1
#
$% −G2 v1 + (G2 + G3 ) v2 = −I 2
Exemplo numérico:
Para R1 = 2Ω , R2 = 5Ω e R3 = 1Ω; I1 = 3 A e
I 2 = −2 A, teremos:
v1 = 5V e v2 = 2,5V
I2
Ref
Designamos uma tensão para cada nó, com
relação ao nó de referência.
1
2
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
Outro exemplo:
Escrevendo a Lei de Kirchhoff das correntes
para os três nós, temos o sistema:
4S
− 3A
$ 7v1 − 3v2 − 4v3 = −11
!
# 3v1 − 6v2 + 2v3 = −3
!4v + 2v − 11v = −25
" 1
2
3
2S
3S
1S
− 8A
Resolvendo esse sistema de equações,
chegamos à
5S
− 25 A
v1 = 1V , v2 = 2V e
Note que podemos reescrever o sistema da
seguinte forma:
Redesenhando
4S
− 3A
2S
v2
v1
v3 = 3V
v3
3S
ou
& 7 − 3 − 4# & v1 # &− 11#
$ − 3 6 − 2 ! $v ! = $ 3 !
$
!$ 2 ! $
!
−
4
−
2
11
v
25
!" $% 3 !" %$
%$
"!
1S
− 8A
$ 7v1 − 3v2 − 4v3 = −11
!
# − 3v1 + 6v2 − 2v3 = 3
!− 4v − 2v + 11v = 25
"
1
2
3
− 25 A
5S
A matriz é simétrica! Isso pode ser usado na
verificação das equações.
Ref
3
4
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
Consideremos agora esse mesmo circuito, mas
com uma fonte de tensão entre os nós 2 e 3:
Para o nó 1:
7v1 − 3v2 − 4v3 = −11.
Super nó
4S
Para super-nó (nós 2 e 3):
− 3A
v1
v2
22V
v3
ou
3(v2 − v1 ) − 3 + 4(v3 − v1 ) + 5v3 − 25 + v2 = 0
− 7v1 + 4v2 + 9v3 = 28.
3S
1S
− 8A
Além disso, sabemos que
− 25 A
v3 − v2 = 22.
5S
Ref
Finalmente:
Dificuldade: não podemos associar a corrente
entre os nós 2 e 3 à tensão do gerador de 22 V
(a tensão do gerador independe da corrente).
• Portanto, não podemos aplicar a Lei de
Kirchhoff das correntes nos nós 2 e 3.
• No entanto: se a soma algébrica das correntes
que saem de um nó é nula, então a soma
algébrica das correntes que saem dos nós 2 e
3 (dito super-nó) também deve ser nula (Lei
de Kirchhoff Generalizada)
5
$ 7v1 − 3v2 − 4v3 = −11
!
#− 7v1 + 4v2 + 9v3 = 28
!
− v2 + v3 = 22
"
Resolvendo, temos
v1 = −4,5V , v2 = −15,5V e
v3 = −6,5V .
6
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
Consideremos agora a presença de um gerador
de tensão dependente:
Resumo – Análise nodal
ix
4S
Procedimento
Super nó
− 3A
v2 i x 8
v1
v3
3S
1S
− 8A
− 25 A
5S
Ref
Novamente, como temos um gerador de tensão
entre os nós 2 e 3, consideraremos este par de
nós como um super-nó. Aplicando a Lei de
Kirchhoff, temos, como antes,
Super-nó:
Nó 1:
− 7v1 + 4v2 + 9v3 = 28
7v1 − 3v2 − 4v3 = −11
Entre os nós 2 e 3:
Ou
v3 − v2 =
− 0,5v1 + v2 − 0,5v3 = 0
Resulta: v1 = 1V , v2 = 2V e
• Redesenhe o circuito, escolhendo um nó
como referência,
• Atribua uma variável a cada um dos outros
nós, para indicar a tensão daquele nó com
relação ao nó de referência,
• Se o circuito contiver apenas fontes de
corrente, escreva a Lei de Kirchhoff das
correntes para cada um dos nós, com exceção
do nó de referência; resolva o sistema de
equações para obter as tensões nos nós.
• Se o circuito contiver fontes de tensão,
escreva a Lei de Kirchhoff generalizada das
correntes para os super-nós formados; além
disso, relacione as tensões dos geradores às
tensões dos nós; resolva o sistema de
equações para obter as tensões nos nós.
ix 4(v3 − v1 )
=
8
8
v3 = 3V
7
8
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
Análise de malhas
Exemplos:
Algumas definições:
Circuito planar: é aquele que pode ser
desenhado em um plano, sem que um ramo
cruze outro.
Exemplo de circuito não planar:
Não é laço
Não é laço
É malha
É laço, mas não é malha
Laço: percurso fechado formado por bipolos e
que não passe duas ou mais vezes pelo mesmo
bipolo ou nó.
Malhas: laços em um circuito plano que não
contém outros laços em seu interior.
Corrente de malha: corrente que circula nos
perímetro de uma malha
9
10
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
Análise de malhas: Aplicação da Lei de
Kirchhoff das tensões nas malhas do circuito,
para obter as correntes de malha.
Repetindo para as outras malhas, chegamos ao
sistema:
$ 3i1 − i2 − 2i3 = 1
!
# − i1 + 6i2 − 3i3 = 0
!− 2i − 3i + 6i = 6
" 1
2
3
Consideremos o circuito abaixo:
i1
i2
que resulta em: i1 = 3 A, i2 = 2 A e i3 = 3 A.
i1 − i2
i2
1Ω
Note que podemos escrever o sistema de
equação por meio de uma equação matricial:
i2 − i3
i1
7V
2Ω
3Ω
6V
2Ω
i3
& 3 − 1 − 2# & i1 # &1#
$ − 1 6 − 3! $i ! = $0!
$
!$ 2 ! $ !
$%− 2 − 3 6 !" $%i3 !" $%6!"
1Ω
i1 − i3
& 3 − 1 − 2#
Matriz de resistência R = $ − 1 6 − 3!
$
!
$%− 2 − 3 6 !"
Três malhas = três equações a partir da Lei de
Kirchhoff das tensões:
Para a malha I:
ou
7 − (i1 − i2 ) − 6 − 2(i1 − i2 ) = 0
3i1 − i2 − 2i3 = 1
11
12
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
Se:
• O circuito contiver apenas fontes de tensão
independentes,
• As correntes de malhas são indicadas no
sentido horário,
• As linhas de R contiverem os coeficientes de
i1 ,i2 … , (ordenados),
• A i-ésima linha corresponde à i-ésima malha,
Não podemos escrever a Lei de Kirchhoff das
tensões para as malhas 1 e 3 (não sabemos
relacionar sua tensão à sua corrente.)
então, R será uma matriz simétrica. Essa
propriedade pode ser um teste para verificar a
correção da matriz.
Consideremos agora a presença de um gerador
de corrente no circuito anterior, ou seja:
Porém, sabemos que i1 − i3 = 7.
Da 2a. malha, temos − i1 + 6i2 − 3i3 = 0
Precisamos de mais uma equação: obtida pela
aplicação da Lei de Kirchhoff das tensões para
o laço formado pelas malhas 1 e 3:
1Ω
7V
i1
7A
1Ω
7V
i1
7A
2Ω
i2
2Ω
2Ω
2Ω
3Ω
i3
1Ω
7 − (i1 − i2 ) + 3(i2 − i3 ) − i3 = 0
3Ω
i3
i1 − i3
i2
% i1 − 4i2 + 4i3 = 7
"
$− i1 + 6i2 − 3i3 = 0 ⇒ i1 = 9 A, i2 = 2,5 A, i3 = 2 A
"
i1 − i3 = 7
#
1Ω
13
14
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
Consideremos, por fim, a presença de um
gerador dependente:
Porém, por inspeção, temos que i1 = 15 A e
i3 − i1 =
1Ω
15 A
i1
i2
2Ω
vx
i3
→ − i1 + 1 i2 + 2 i3 = 0,
3
3
completando o conjunto de equações
necessário, resultando em:
3Ω
vx
9
2Ω
vx
9
i1 = 15 A, i2 = 11A e i3 = 17 A.
1Ω
Como antes, precisamos de três equações
relacionando as correntes de malha. A primeira
pode ser obtida da malha 2:
ou
1(i2 − i1 ) + 2i2 + 3(i2 − i3 ) = 0
− i1 + 6i2 − 3i3 = 0
Seguindo o procedimento adotado para o caso
da presença de gerador de corrente (abrir o
circuito naquele ponto), resulta em um circuito
com apenas a malha 2, de onde já extraímos
uma equação.
15
16
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 3
Resumo – Análise de mlaha
Procedimento
Esse método é válido apenas para circuitos
planos.
• Indique as correntes de malha,
• Se o circuito contiver apenas geradores de
tensão, escreva a Lei de Kirchhoff das tensões
para cada uma das malhas e resolva o sistema
de equações obtido.
• Se o circuito contiver geradores de corrente,
substitua-os por circuitos abertos (o que reduz
o número de malhas), escreva a Lei de
Kirchhoff para as malhas restantes e resolva o
sistema de equações obtido.
17