X Encontro Nacional de Educação Matemática A

X Encontro Nacional de Educação Matemática
Educação Matemática, Cultura e Diversidade
Salvador – BA, 7 a 9 de Julho de 2010
A EXPRESSÃO GRÁFICA NA EXPLORAÇÃO DE PROPRIEDADES
GEOMÉTRICAS ATRAVÉS DE SOFTWARE DE GEOMETRIA DINÂMICA
Anderson Roges Teixeira Góes
Universidade Federal do Paraná - Departamento de Expressão Gráfica; e
Secretaria Municipal de Educação de Araucária/PR – Tecnologia Educacional, Brasil.
[email protected]
Marco Antonio da Cunha
Universidade Federal do Paraná – Departamento de Expressão Gráfica,
Programa Licenciar, Brasil.
[email protected]
Adriana Augusta Benigno dos Santos Luz, Heliza Colaço
Universidade Federal do Paraná – Departamento de Expressão Gráfica,
Programa de Pós-Graduação em Educação em Ciências e em Matemática, Brasil.
[email protected], [email protected]
Resumo. Este artigo relata uma metodologia de ensino de Geometria através do software
de Geometria Dinâmica (GD) “Régua e Compasso versão Metal”. A utilização de software
de GD é uma ferramenta de suma importância para o ensino e aprendizado de Geometria,
uma vez que esta metodologia proporciona ao aluno uma experiência impossível no
aprendizado tradicional, pois o aluno pode ver instantaneamente as modificações em suas
construções. O exemplo didático apresentado neste artigo exemplifica o potencial desta
metodologia mostrando em sala o ganho imediato na compreensão dos conteúdos que
ficavam anteriormente apenas no imaginário.
Palavras-chave: Geometria Dinâmica; Ensino da Matemática; Expressão Gráfica.
1. Introdução
Com a perspectiva de que o mundo atual exige uma formação que tenha significado
para o cidadão e sintonize-o com uma visão de mundo diferente, para assim garantir uma
formação que o torne o protagonista na construção do conhecimento, criou-se uma
metodologia aplicada no curso de Matemática da Universidade Federal do Paraná, para a
disciplina de Geometria Dinâmica (GD).
O exemplo aqui relatado utiliza o software “Régua e Compasso versão Metal” e
possui como objetivo trabalhar os conhecimentos das propriedades de triângulos e
quadriláteros adquiridos na disciplina de Desenho Geométrico I. As interações propostas
X Encontro Nacional de Educação Matemática
Educação Matemática, Cultura e Diversidade
Salvador – BA, 7 a 9 de Julho de 2010
levam os alunos a uma experimentação destes conteúdos de uma forma impossível no
desenho tradicional.
O desenvolvimento de metodologias alternativas cria elo entre a teoria e prática em
sala de aula, oportunizando aos alunos a construção e verificação de conhecimento, com
grande participação em sala de aula. (GÓES, 2004)
Assim, este artigo relata experiência desenvolvida nas aulas de Matemática com
alunos do 4º período do curso de Matemática, onde através da GD consolidaram os
conhecimentos de Geometria.
2. Revisão de literatura
A Tecnologia possui diversas funções na sociedade e cada vez mais conquista um
maior espaço na educação.
É visível que muitos Educadores Matemáticos não estão alheios a esta conquista e
desenvolvem metodologias de ensino em que a Tecnologia Educacional é uma ferramenta
indispensável no processo ensino-aprendizado.
Vários são os artigos que relatam estas metodologias/experiências do ensino da
Matemática assistido por computador, entre eles podemos citar: Borges Neto (2009), Góes
et al. (2009), Barbosa et al. (2007), Pongelupe et al. (2004), Angelo e Rigodanzo (2004) e
Gravina (1996).
No trabalho desenvolvido por Borges Neto (2009), o autor afirma que é importante
oportunizar o acesso à tecnologia às crianças, pois com a experiência realizada as crianças
foram estimuladas a apropriar-se dos conhecimentos. Ao arrastar as figuras e observarem
suas transformações, puderam comparar, sintetizar e formular “enunciados conceituais”.
Não foi percebido o desenvolvimento significativo das estruturas mentais, mas foi evidente
a progressiva melhora na elaboração de conceitos e demonstração de seu pensamento. No
entanto, enfatizam que momentos/intervenções com o professor devem estar vinculados às
atividades para que se possam sintetizar os conhecimentos adquiridos espontaneamente e
assim relacioná-los com os conhecimentos científicos do assunto.
Barbosa et al. (2007), desenvolvem atividades respaldadas pela metodologia de
resolução de problemas, cujos objetivos são estimular os alunos a realizarem suas próprias
observações e despertar a busca de generalizações matemáticas. Afirmam que a GD,
X Encontro Nacional de Educação Matemática
Educação Matemática, Cultura e Diversidade
Salvador – BA, 7 a 9 de Julho de 2010
através da livre exploração, torna mais significativa o conhecimento do software, uma vez
que as descobertas individuais geram maior motivação na manipulação. Ao movimentar
uma construção se vê claramente as propriedades geométricas da figura, diferentemente da
construção no papel onde temos um referencial estático. Assim, concluem que a
implementação deste tipo de metodologia de ensino é um grande desafio ao professor, pois
insere uma nova maneira de pensar a matemática não restrita a aplicação de
procedimentos.
Para Gravina (1996), os livros didáticos, em sua maioria, iniciam o ensino de
Geometria com definições acompanhadas de desenhos bem particulares. Esses desenhos,
não estimulam nos alunos o raciocínio. Um exemplo particular apresentado pela autora é o
polígono “quadrado” em que na maioria dos livros é apresentado com seus lados paralelos
à margem da folha. No entanto, ao apresentar um quadrado rotacionado a maioria absoluta
dos alunos não sabe afirmar se a figura é um quadrado, pois acreditam que a posição
relativa do desenho e/ou seu traçado particular são características do objeto, ocorrendo
desequilíbrio na formação dos conceitos. Isto se deve ao fato que dificilmente os livros
apresentam instruções "construa", que é uma das atividades que leva o aluno ao domínio de
conceitos geométricos.
Uma metodologia para sanar o problema apontado pela autora acima pode ser vista
no trabalho desenvolvido por Pongelupe et al. (2004), onde utiliza a motivação visual de
software de GD a construir conceitos matemáticos. Os autores afirmam que os conceitos
construídos com software estimulam o uso da ferramenta para novas descobertas pelos
alunos, que através da metodologia utilizada realizam a análise da relação entre tais
construções.
No entanto, vê-se que é necessária a formação dos professores e sobre este assunto
Góes et al. (2009) e Angelo e Rigodanzo (2004) afirmam que ao final de encontros de
Formação de professores, os participantes demonstram estar motivados e interessados na
continuidade da proposta de discussão e desenvolvimento de atividades a serem aplicadas
em sala de aula com utilização de softwares. Os autores afirmam que a necessidade de
tempo é uma das características do uso dessas ferramentas para que permita a vivência,
autonomia e segurança do professor para a elaboração de atividades que façam o aluno
apropriar-se do conhecimento por meio do ambiente computacional.
X Encontro Nacional de Educação Matemática
Educação Matemática, Cultura e Diversidade
Salvador – BA, 7 a 9 de Julho de 2010
3. Exemplo didático de utilização da Geometria Dinâmica no Ensino Superior
Para a aplicação desta metodologia foi proposto aos alunos o seguinte exercício de
construção:
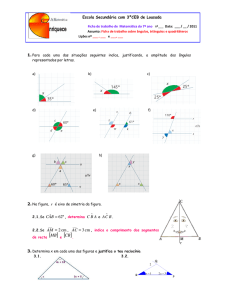
“Construa um triângulo ∆ABC qualquer e os pontos médios M, N e P dos
lados AB, AC e BC, respectivamente. Construa os pontos D e E, pontos
médios de BP e PC. Construa o quadrilátero DENM .
É possível que o quadrilátero DENM seja um paralelogramo, retângulo,
losango, ou quadrado? Se for possível, qual a condição imposta ao triângulo
ABC para que isto ocorra”.
Figura 01 – Triângulo ABC e quadrilátero DENM
3.1. Construção do exercício e primeiras explorações
A primeira etapa da atividade é a construção do triângulo ∆ABC e do quadrilátero
DENM (figura 01) que requer os conhecimentos de ponto médio e outros conhecimentos
básicos do software “Régua e Compasso versão Metal”.
Nesta etapa o papel do professor consiste em auxiliar os alunos na utilização do
software indicando as diversas ferramentas que podem ser utilizadas para obter o resultado
esperado.
Em seguida os alunos são desafiados com a seguinte indagação: o quadrilátero
DENM possui alguma regularidade?
A resposta para a pergunta acima exige conhecimentos como propriedades dos
triângulos, mediana, mediatriz, ângulos alternos-internos e classificação das formas de
quadriláteros, já adquiridos na disciplina de Desenho Geométrico I.
Ao explorar a figura o aluno é capaz de observar que o quadrilátero DENM é um
paralelogramo, pois o lado MN é paralelo ao lado BC e o lado DM é paralelo ao lado EM,
X Encontro Nacional de Educação Matemática
Educação Matemática, Cultura e Diversidade
Salvador – BA, 7 a 9 de Julho de 2010
sendo estas afirmações justificadas pela utilização da ferramenta “Testar – Retas
paralelas?” e pela propriedade P1 de triângulos:
“O segmento que une os pontos médios de dois lados de um triângulo é
paralelo ao terceiro lado e sua medida é igual à metade do comprimento do
lado a que é paralelo”
Como MN é paralelo a DE por P1 (figura 02) e DM é paralelo a EN por P1 (figura
03), tem-se que o quadrilátero DENM é um paralelogramo, logo MN e DE são
congruentes (propriedade de paralelogramos) e medem metade de BC (por P1). As
primeiras justificativas (MN é paralelo a DE e DM é paralelo a EN) podem ser
comprovadas utilizando a ferramenta “ângulos” e assim verificando que os ângulos
alternos-internos são iguais.
Figura 02 - MN paralelo a DE
Figura 03 - DM paralelo a EN
X Encontro Nacional de Educação Matemática
Educação Matemática, Cultura e Diversidade
Salvador – BA, 7 a 9 de Julho de 2010
Tem-se também quem DM e EN é paralelo a AP. A justificativa é por P1, pois o
lado DM é paralelo à AP, uma vez que ao considerarmos o triângulo PAB tem-se que D é
ponto médio de BP e M é ponto médio de AB. De forma análoga tem-se EN paralelo a AP.
(figura 03).
Com base nas observações acima, a próxima etapa da atividade consiste em
identificar as possibilidades de regularidade do paralelogramo DENM , onde o professor
indagou se é possível este paralelogramo ser transformado em retângulo, losango ou
quadrado ao mover um dos vértices do triângulo ABC.
3.2. Condição para que o quadrilátero DENM seja um retângulo
Com a ferramenta “mover ponto” do software “Régua e Compasso”, os alunos
podem alterar o triângulo pelos seus vértices e assim verificar as mudanças que ocorrem no
quadrilátero.
Fixando BC e movendo o ponto A, verifica-se que medida que o vértice A
aproxima-se da mediatriz relativa à BC, a forma do quadrilátero aproxima-se de um
retângulo.
Intuitivamente o aluno percebe que o paralelogramo DENM é um retângulo quando
a mediana relativa ao vértice A forma ângulo reto com a base BC (figura 04).
Figura 04 – AP ortogonal a BC
Assim, quando a mediana relativa ao vértice A é ortogonal a base BC tem-se os
lados DM e EM ortogonais ao lado DE o que satisfaz a condição para que o paralelogramo
DENM seja um retângulo.
X Encontro Nacional de Educação Matemática
Educação Matemática, Cultura e Diversidade
Salvador – BA, 7 a 9 de Julho de 2010
3.3. Condição para que o quadrilátero DENM seja um losango
Pela definição de Losango, o paralelogramo DENM deve possuir seus lados
congruentes, ou seja, DM = DE = EN = NM .
Utilizando a ferramenta “exibir valores” e movendo os vértices do triângulo para
que os lados do paralelogramo DENM sejam iguais, verifica-se que as medidas de AP e
BC são iguais.
A justificativa da afirmação acima se deve ao fato de já termos mostrado que
DM = EN , BC = 2 × DE e AP = 2 × DM . Assim,
BC = 2 × DE
BC = 2 × DM
BC = 2 ×
AP
2
BC = AP
Logo, para que quadrilátero DENM seja um losango deve-se ter BC = AP .
Portanto A deve pertencer a circunferência de centro P e raio BC .
Figura 05 – DE=EN=NM=MD
3.4. Condição para que o quadrilátero DENM seja um quadrado
Utilizando a definição que quadrado é o “quadrilátero que possui lados iguais e 4
ângulos congruentes” temos que o paralelogramo DENM precisa ser um retângulo e
losango simultaneamente.
Logo, como mostrado nas seções anteriores deve-se ter AP perpendicular a BC e
BC = AP .
X Encontro Nacional de Educação Matemática
Educação Matemática, Cultura e Diversidade
Salvador – BA, 7 a 9 de Julho de 2010
4. Considerações Finais
Explorar atividades utilizando software de GD é atrativa e torna a aprendizagem
significativa, uma vez que o aluno tem autonomia de manipular a construção e elaborar
conclusões e observações de forma natural, não necessitando, muitas vezes, da mediação
do professor. Ainda, o potencial desta metodologia mostra em sala o ganho imediato na
compreensão dos conteúdos que, anteriormente, ficavam apenas no imaginário.
Percebe-se que os questionamentos de turmas anteriores, onde foram aplicados
exercícios para explorar propriedades geométricas sem auxílio de GD, não surgiram
durante a aplicação deste. Isto deve-se ao fato que neste tipo de atividade investigativa os
alunos esgotam todas as possibilidades de exploração antes de solicitar uma mediação,
realizam a si mesmo os questionamentos e buscam soluções e tornam-se autônomos na
aprendizagem, ou seja, os alunos constroem os conhecimentos.
Com este tipo de atividade proporcionamos aos alunos (futuros profissionais da
educação) uma metodologia diferente da tradicional e com isso esperamos que estes
utilizem a GD em suas aulas para que haja melhoria da qualidade do ensino e,
conseqüentemente, a melhoria da prática de ensino, pois o uso da GD permite um melhor
aproveitamento da aula, uma vez que o professor deixa de ser um reprodutor de conteúdos
e passar a ser um mediador na apropriação do conhecimento.
Este trabalho mostra uma mudança de postura e atitude, no que concerne à
educação, fruto desse conjunto de vivências e experiências construídas da prática diária.
Assim, concluímos que a melhoria da qualidade do ensino e, conseqüentemente, da
melhoria da prática de ensino envolve muitas questões como, por exemplo, a formação
continuada de professores e a utilização de recursos de novas tecnologias em sala de aula.
Referências
ANGELO, C. L.; RIGODANZO, M. Uma experiência de transposição didática com o
Cabri-Géomètre. Educação Matemática em Revista. São Paulo, SBEM, n.16, p. 16-24,
mai, 2004.
BARBOSA, A. C. M.; COSTA, B. O.; POSSAS, C. S.; LIMA, D. C. de A. Semelhança e
área de figuras planas com Geometria Dinâmica. In: IX Encontro Nacional de
Educação Matemática. Belo Horizonte, 2007
X Encontro Nacional de Educação Matemática
Educação Matemática, Cultura e Diversidade
Salvador – BA, 7 a 9 de Julho de 2010
BORGES NETO, H. Construindo conceitos matemáticos com o Cabri-Géomètre.
Disponível em <www.multimeios.ufc.br/arquivos/pc/pre-print/cabri.pdf> Acessado em 01
de jun. de 2009.
GÓES, A. R. T. Desenho Técnico – Engenharia Civil – “Uma proposta metodológica”.
Curitiba, 2004. Monografia (Especialização em Desenho Aplicado ao Ensino da Expressão
Gráfica) – Setor de Ciências Exatas, Universidade Federal do Paraná.
GÓES, A. R. T.; TELES, L. S. J.; LAGO, R. C.;COLAÇO, H. Geometria Dinâmica e a
Formação Continuada de Professores na Tecnologia Educacional. In: VIII
International Conference on Graphics Engineering of Arts and Design. Bauru/SP, 2009
GRAVINA, M. A. Geometria Dinâmica: Uma Nova Abordagem para o Aprendizado
da Geometria. In: VII Simpósio Brasileiro de Informática na Educação, p. 1-13. Belo
Horizonte, 1996
PONGELUPE, E. G.; MELO, M. C. R.; LANNES, W. Uma proposta alternativa de
aprendizagem motivada pela experimentação através da geometria dinâmica. Revista
Educação e Tecnologia, v.9, n.1, p.42-48. Belo Horizonte, 2004