1. Uma amostra de um gás está contida em um cilindro ao qual se

Professora Florence Monteiro
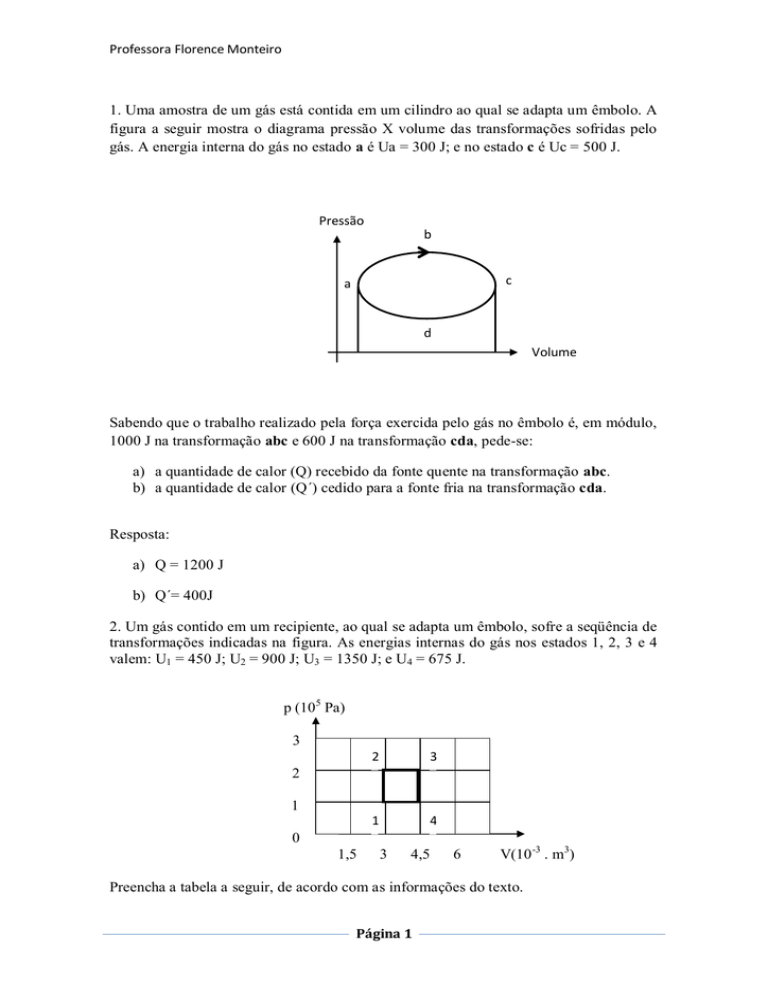
1. Uma amostra de um gás está contida em um cilindro ao qual se adapta um êmbolo. A
figura a seguir mostra o diagrama pressão X volume das transformações sofridas pelo
gás. A energia interna do gás no estado a é Ua = 300 J; e no estado c é Uc = 500 J.
Pressão
b
c
a
d
Volume
Sabendo que o trabalho realizado pela força exercida pelo gás no êmbolo é, em módulo,
1000 J na transformação abc e 600 J na transformação cda, pede-se:
a) a quantidade de calor (Q) recebido da fonte quente na transformação abc.
b) a quantidade de calor (Q´) cedido para a fonte fria na transformação cda.
Resposta:
a) Q = 1200 J
b) Q´= 400J
2. Um gás contido em um recipiente, ao qual se adapta um êmbolo, sofre a seqüência de
transformações indicadas na figura. As energias internas do gás nos estados 1, 2, 3 e 4
valem: U1 = 450 J; U2 = 900 J; U3 = 1350 J; e U4 = 675 J.
p (105 Pa)
3
2
3
1
4
2
1
0
1,5
3
4,5
6
V(10 -3 . m3)
Preencha a tabela a seguir, de acordo com as informações do texto.
Página 1
Professora Florence Monteiro
Transformação
Tipo
Expressão para
o cálculo
Substituições
numéricas
Resposta (J)
12
23
34
41
1  2  3 4
1
3. (UFOP-MG) Um gás perfeito descreve o ciclo ABCD como indica a figura.
Determine o trabalho que o sistema troca com o meio nas transformações:
a) AB
b) BC
p (N/m2)
c) CD
d) DA
e) ABCDA
A
B
3
2
1
C
D
V (m3)
1
2
Resposta:
a) T = 6,0 J
b) T = 0
c) T = - 2,0 J
d) T = 0
e) Tciclo = 4,0 J
Página 2
3
Professora Florence Monteiro
4. (UFBA) Uma certa massa de gás ideal sofre a transformação cíclica reversível
ABCA, conforme o diagrama de p X V apresentado na figura. Determine o trabalho
realizado em cada transformação.
p (105N/m2)
B
6
4
C
A
V (m3)
10
20
30
TAB = 0
TBC =1 x 10-7 J
TCA= - 8 x 106 J
5. Uma massa de gás ocupa volume de 4 litros sob pressão de 2 x 106 N/m2 . Após
receber 500 J de calor, mantendo constante a pressão, o volume passa a 10 litros.
Determine a variação de energia interna do gás.
Resposta:
- 11500 J
6. O gráfico a seguir mostra como varia a energia interna de um mol de oxigênio numa
transformação isométrica, quando a sua temperatura varia de 200 K a 300 K. Determine
a quantidade de calor absorvida pelo gás na transformação.
U (cal)
1500
1000
T (K)
200
300
Página 3
Professora Florence Monteiro
Resposta: Q = 500 cal
7. (Uem 2012) Sobre as transformações termodinâmicas que podem ocorrer com um
gás ideal confinado em um cilindro com pistão, assinale o que for correto.
01) Um gás ideal realiza trabalho ao se expandir, empurrando o pistão contra uma
pressão externa.
02) Em uma transformação adiabática ocorre troca de calor com a vizinhança.
04) A energia interna de uma amostra de gás ideal não varia, quando este sofre uma
transformação isovolumétrica.
08) Quando o gás ideal sofre uma compressão, o trabalho é realizado por um agente
externo sobre o gás ideal.
16) O gás ideal não realiza trabalho em uma transformação isovolumétrica.
Resposta:
01 + 08 + 16 = 25.
01) Correta. Devido à pressão, o gás exerce força sobre o êmbolo, empurrando o
pistão, realizando trabalho positivo.
02) Incorreta. Transformação adiabática é aquela em que o gás não troca calor com a
vizinhança.
04) Incorreta. A energia interna de um gás ideal depende exclusivamente da sua
temperatura absoluta. Portanto, somente não ocorre variação da energia interna,
quando a transformação é isotérmica.
08) Correta. Na compressão o gás recebe trabalho de um agente externo.
16) Correta. Se a transformação é isovolumétrica, não ocorre deslocamento do pistão,
não havendo realização de trabalho.
Página 4
Professora Florence Monteiro
8. (Unifesp 2011) Em um trocador de calor fechado por paredes diatérmicas,
inicialmente o gás monoatômico ideal é resfriado por um processo isocórico e depois
tem seu volume expandido por um processo isobárico, como mostra o diagrama pressão
versus volume.
a) Indique a variação da pressão e do volume no processo isocórico e no processo
isobárico e determine a relação entre a temperatura inicial, no estado termodinâmico
a, e final, no estado termodinâmico c, do gás monoatômico ideal.
b) Calcule a quantidade total de calor trocada em todo o processo termodinâmico abc.
Resposta:
a) No processo isocórico (volume constante) (a  b):
Variação do volume: Δ Vab = Vb – Va = 0
Variação da pressão: Δ Pab = Pb – Pa = (1,0 – 3,0)  105  Δ Pab = –2,0  105 Pa.
No processo isobárico (pressão constante) (b  c):
Variação do volume: Δ Vbc = Vc – Vb = (6,0 – 2,0)  10–2  Δ Vab = 4,0  10–2 m3.
Variação da pressão: Δ Pbc = Pc – P b = 0.
Aplicando a equação geral dos gases entre os estados a e c.
Pa Va Pc Vc

Ta
Tc

6  10 3
6  10 3

Ta
Tc
3  105  2  102 1 105  6  102


Ta
Tc

Ta  Tc

Ta
 1.
Tc
b) Sendo Q a quantidade de calor trocado, Δ U a variação da energia interna e W o
trabalho realizado entre dois estados, a 1ª lei da termodinâmica nos dá:
Q = Δ U + W.
Como mostrado no item anterior, a temperatura do gás nos estados a e c são iguais,
portanto a variação da energia interna entre esses dois estados é nula ( Δ Uac = 0).
Então:
Página 5
Professora Florence Monteiro
Qac = Wac = Wab + Wbc.
Mas a transformação ab é isocórica  Wab = 0. Então:
Qac = Wbc = Pc (Vbc) = 1,0  105  4,0  10–2 
Qac = 4,0  103 J.
9. (Epcar (Afa) 2011) O diagrama abaixo representa um ciclo realizado por um sistema
termodinâmico constituído por n mols de um gás ideal.
Sabendo-se que em cada segundo o sistema realiza 40 ciclos iguais a este, é correto
afirmar que a(o)
a) potência desse sistema é de 1600 W.
b) trabalho realizado em cada ciclo é - 40 J.
c) quantidade de calor trocada pelo gás com o ambiente em cada ciclo é nula.
d) temperatura do gás é menor no ponto C.
Resposta:
[A]
A frequência de operação é 40 ciclos/s, ou seja, 40 Hz. Notemos ainda que, no eixo das
abscissas o volume está em litro. (1 L = 10 –3 m3).
Calculando o trabalho (Wciclo) em cada ciclo. Como se trata de um ciclo no sentido
horário, o trabalho realizado é positivo, sendo numericamente igual á “área” interna do
ciclo.
Wciclo  " Área"   0,6  0,2 2  1  105  103  Wciclo  40 J.
O trabalho total (W) em 40 ciclos é:
W  40  40   1.600 J.
Calculando a potência do sistema:
P
W 1.600 J

t
1s
 P  1.600 W.
Página 6
Professora Florence Monteiro
10. (Ufpe 2011) Um gás ideal se transforma de acordo com o ciclo termodinâmico
mostrado abaixo no diagrama pressão versus volume. Os processos AB e CD são
isovolumétricos, e os processos BC e DA são isotérmicos. Qual a razão TC /TD entre as
respectivas temperaturas absolutas do gás nos pontos C e D?
Resposta:
A transformação AB é isométrica. Então, para os estados A e B:
pA pB

TA TB

0,5 2,5

TA
TB

TB
 5.
TA
Como as transformações BC e DA são isotérmicas, TB  TC e TD  TA . Então:
TC TB

 5.
TD TA
11. (Ufjf 2011) A figura abaixo mostra o diagrama P x V para o ciclo de um sistema
termodinâmico contendo um gás ideal monoatômico.
a) Calcule o trabalho total, em joules, realizado pelo gás no ciclo completo.
b) Calcule a variação da energia interna, em joules, no percurso AB.
c) Qual é a quantidade de calor, em joules, trocada pelo sistema no percurso AB?
Página 7
Professora Florence Monteiro
Resposta:
Dados: 1 atm  105 N/m2 .
a) O trabalho no ciclo é dado pela “área” do ciclo.
Wciclo  1 0,04   1 0,02  105  Wciclo  6.000 J.
b) Como se trata de uma transformação isobárica, a variação da energia interna pode ser
calculada pela expressão:
3
3
P VAB   3  105  0,04 
2
2
UAB  18.000 J.
UAB 
c) Aplicando a 1ª lei da termodinâmica para a transformação AB:
QAB  WAB  UAB  P VAB  18.000  3  105  0,04  18.000  12.000  18.000 
QAB  30.000 J.
12. (Ufg 2010) A máquina térmica é um dispositivo que pode tanto fornecer energia
para um sistema quanto retirar.
Considere que a máquina térmica opera com um gás ideal em um sistema fechado,
conforme o ciclo ilustrado acima. De acordo com o exposto,
a) calcule o trabalho total em ciclo;
b) explique como ela opera, ou seja, qual é a sua função? Justifique sua resposta;
c) calcule a temperatura no ponto C, considerando que a temperatura do ponto A é de
300 K.
Resposta:
a) Como o ciclo é anti-horário, o trabalho realizado é negativo e seu módulo é dado pela
área interna ao ciclo, que forma um trapézio.
Wciclo = -ATrap = –
(VB  VA )  (VC  VD )
(pD  pA )  Wciclo = –
2
(3  1)  (2,5  2)
(2  1)  105 
2
Wciclo = -1,25  105 J.
Página 8
Professora Florence Monteiro
b) Como o trabalho é negativo, o sistema gasoso está recebendo trabalho, operando
como refrigerador.
c) Aplicando a equação geral dos gases ideais:
pC VC pA VA

TC
TA
 TC 
pC VC TA 2  105  2,5  300

pA VA
1 105  1
 TC = 1.500 K.
13. (Uece 2010) No diagrama P-V a seguir, quatro processos termodinâmicos cíclicos
executados por um gás, com seus respectivos estados iniciais, estão representados. O
processo no qual o trabalho resultante, realizado pelo gás é menor é o
a) I.
b) J.
c) K.
d) L.
Resposta:
[C]
O trabalho (W) realizado numa transformação cíclica é numericamente igual à área
interna do ciclo. A área interna dos ciclos I, J e L corresponde à de 4 quadrículos. A
área do ciclo K é menor que a de 4 quadrículos.
Podemos também efetuar os cálculos:
WI = 1  4 = 4 J;
WJ = 2  2 = 4 J;
WK = 3,14  12 = 3,14 J;
WL = 2  2 = 4 J.
Página 9